连续型随机变量函数的分布
例19 设X为连续型随机变量,其概率密度为fX(x),试求X的线性函数Y=aX+b(a≠0)的概率密度.
解 设Y的分布函数为FY(y),则
![]()
下面分两种情况来讨论.
(1)a>0,这时
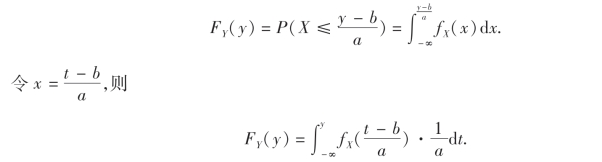
于是得到Y=aX+b的概率密度为
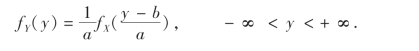
(2)a<0,这时
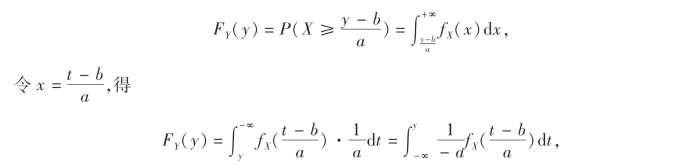
所以Y=aX+b的概率密度为

把两种情形的结果统一起来,可写成
![]()
例如,设X ~N(μ,σ2),即X的概率密度为
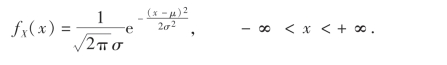
则Y=aX+b的概率密度为

一般有下面的定理.
定理2 设X是一个连续型随机变量,其概率密度为fX(x).若y=g(x)为一严格单调函数,其反函数x=h(y)有连续导数,则Y=g(X)也是一个连续型随机变量,且概率密度为

其中α=min{g(-∞),g(+∞)}, β=max{g(-∞),g(+∞)}.
证 设y=g(x)为严格单调上升函数,其值域为(α,β),其中α=g(-∞),β=g(+∞),则它的反函数x=h(y)在(α,β)内有定义,且也是严格单调增函数.下面先求Y=g(X)的分布函数FY(y):
当y≤α时,{Y≤y}={g(X)≤y}为不可能事件,故
![]()
当y≥β时,{Y≤y}={g(X)≤y}为必然事件,从而
![]()
当α <y<β时,{Y≤y}={g(X)≤y}={X≤h(y)},故
![]()
令x=h(t),则
![]()
于是得到Y的概率密度为

同理可证当y=g(x)为严格单调减函数时,有
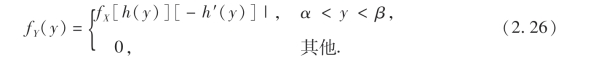
因为当g(x)严格单调增时,h′(y)≥0;当g(x)严格单调减时,h′(x)≤0,所以(2.25)与(2.26)两式可统一写成(2.24)式.证毕.
当fX(x)在有限区间[a,b]之外取值为零时,只需假设在[a,b]上g(x)严格单调,反函数具有连续导数,则定理2的结论同样成立.此时
![]()
例20 设随机变量X在区间[0,1]上服从均匀分布,试求Y=eX的概率密度.解 X的概率密度为

即
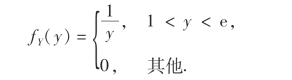
例21 设X ~N(0,1),试求Y=X2的概率密度.
解 X的概率密度为
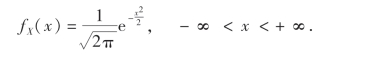
由于y=x2在(-∞,+∞)内不是单调函数,故不能用公式(2.24)来求Y=X2的概率密度.下面我们先求Y=X2的分布函数FY(y).
当y≤0时,显然
![]()
当y>0时有
![]()

最后,我们指出,连续型随机变量X的函数Y=g(X)不一定是连续型的.如果它是离散型的,那么我们可以根据分布律的定义来计算Y的分布.
例22 设加工零件的尺寸误差X~N(0,σ2),有时正误差和负误差所产生的后果不同.若用Y表示由误差引起的损失,为简单计,可设

这里a≠b,求Y的分布律.
解 易知Y的取值为a和b,且
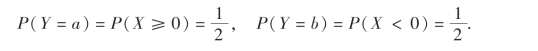
这里的Y是一个离散型随机变量,它服从两点分布.
