* §4.4 矩和协方差矩阵
前几节我们已讨论了随机变量的几个重要的数字特征，但它们并不能完全刻画随机变量的分布特征，在数理统计中还要用到其他数字特征，为此引入矩的概念.
定义6 设X与Y是随机变量，若E（Xk）（k=1，2，…）存在，则称它为X的k阶原点矩，简称k阶矩；若E｛［X-E（X）］k｝（k=1，2，…）存在，则称它为X的k阶中心矩；若E（XkYl）（k，l=1，2，…）存在，则称它为X和Y的k+l阶混合矩；若E｛［X-E（X）］k［YE（Y）］l｝（k，l=1，2，…）存在，则称它为X和Y的k+l阶混合中心矩.
显然，随机变量X的一阶原点矩就是它的数学期望E（X），二阶中心矩就是它的方差D（X），而协方差Cov（X，Y）是X和Y的二阶混合中心矩.
根据矩的定义，矩是特定的期望，因此，在计算矩时只要按期望的求法即可.
例22 设X ～N（0，1），求E（Xk）.
解
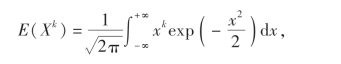
当k=奇数时，利用对称性知E（X）=0；
当k=偶数时，利用分部积分法：
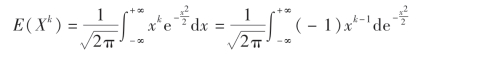
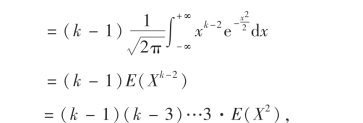
其中E（X2）=D（X）-［E（X）］2=1+0=1，所以
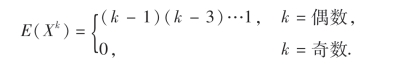
为了研究高维随机向量的概率分布及性质，我们引入协方差矩阵，它可使多维随机向量的概率密度表达式采用简捷的矩阵表示.
定义7 设n维随机向量为X=（X1，X2，…，Xn）′，若其每个分量的数学期望都存在，则称E（X）=［E（X1），E（X2），…，E（Xn）］′为n维随机向量X的数学期望向量，简称X的数学期望，而称
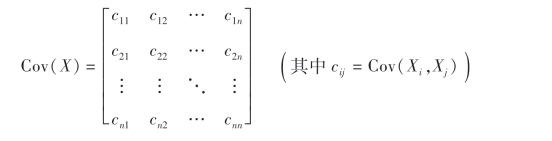
为n维随机向量X的协方差矩阵.
协方差矩阵具有以下性质：
性质1 n维随机向量X的协方差矩阵Cov（X）是对称阵；
性质2 cii=D（Xi）， （i=1，2，…，n）；
性质3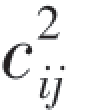 
≤cii·cjj， （i，j=1，2，…，n）；
性质4 n维随机向量X的协方差矩阵Cov（X）=［Cov（Xi，Xj）］n×n是非负定矩阵.
证 设对于任意的n维实向量A=（a1，a2，…，an）′，有
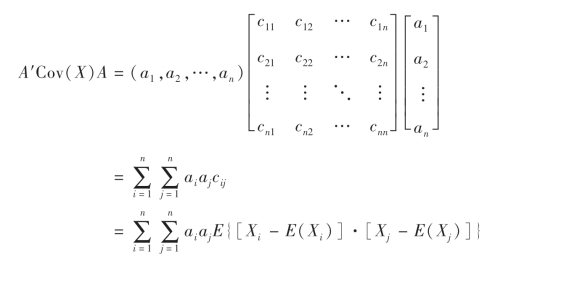
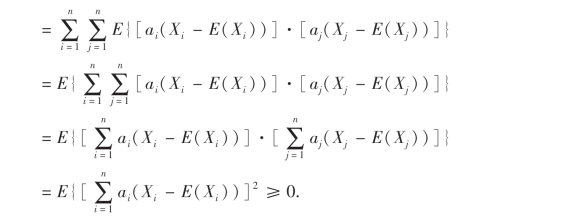
例23 设二维随机向量X=（X1，X2）～N（μ1，μ2；σ1，σ2；ρ），试用协方差矩阵Cov（X）表示它的概率密度函数，并推广到n维正态分布的情形.
解 二维正态随机向量的概率密度函数为
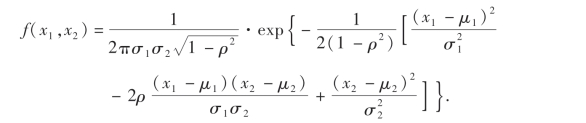
因为（X1，X2）～N（μ1，μ2；σ1，σ2；ρ），则
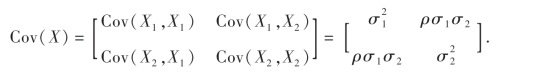
从而
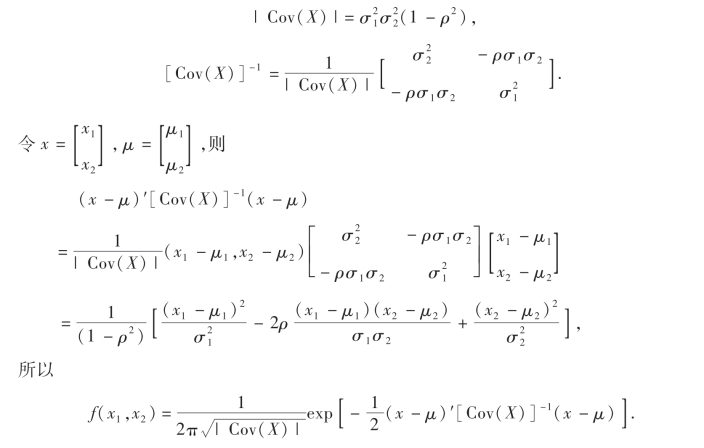
上式容易推广到n维随机向量（X1，X2，…，Xn）的情形，令
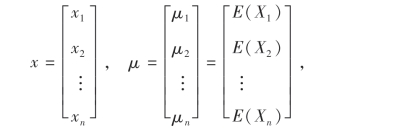
则n维正态随机向量（X1，X2，…，Xn）的概率密度函数为
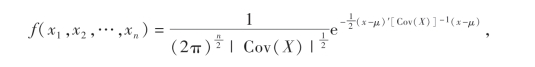
其中Cov（X）是（X1，X2，…，Xn）的协方差矩阵.