§3.2 边缘分布
二维随机变量（X，Y）作为一个整体，它具有分布函数F（x，y），而X和Y都是随机变量，也有各自的分布函数，分别记为FX（x），FY（y），依次称它们为二维随机变量（X，Y）关于X和Y的边缘分布函数.
首先注意到，边缘分布函数可以由（X，Y）的分布函数F（x，y）唯一确定，这是因为
即只要在函数F（x，y）中令y→+∞就能得到FX（x）.
同理有
对于二维离散型随机变量（X，Y），设它的分布律为P（X=xi，Y=yj）=pij，i，j=1，2，…，于是
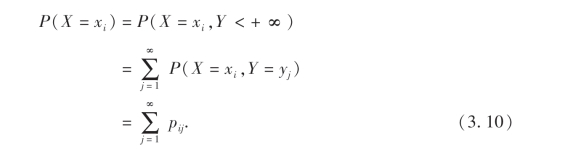
同理有
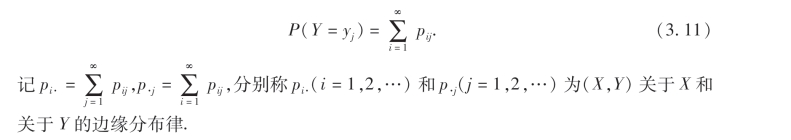
对于二维连续型随机变量（X，Y），设它的概率密度为f（x，y），由
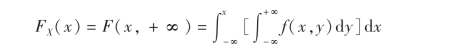
知道，X是一个连续型随机变量，且其概率密度为
同样，Y也是一个连续型随机变量，其概率密度为
分别称fX（x），fY（y）为（X，Y）关于X和Y的边缘概率密度.
例5 在10件产品中，有2件一级品、7件二级品、1件次品.从中抽取3件，设X，Y分别表示抽得的一级品和二级品的件数，求（X，Y）的分布律及边缘分布律.
解 X可能取0，1，2；Y可能取0，1，2，3.
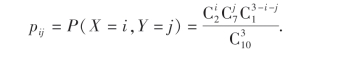
其中i=0，1，2；j=0，1，2，3；且2≤i+j≤3.
当i+j≤1或i+j≥4时，“X=i，Y=j”为不可能事件，故pij=0.
由上述算得的分布律及边缘分布律如下表：
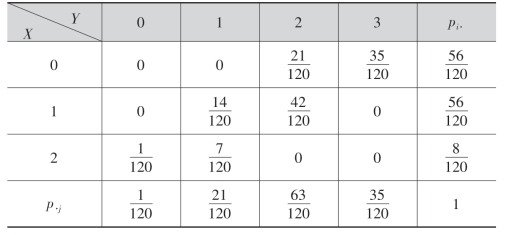
我们常把边缘分布律写在联合分布律表格的边缘上，如上表所示，这种方法求边缘分布律较简单直观.这就是“边缘分布律”这个名称的来源.
例6 设随机变量（X，Y）的概率密度为
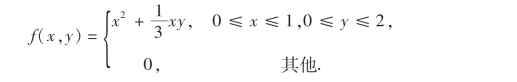
求（X，Y）关于X及关于Y的边缘概率密度.
解 由（3.12）及（3.13）式，得
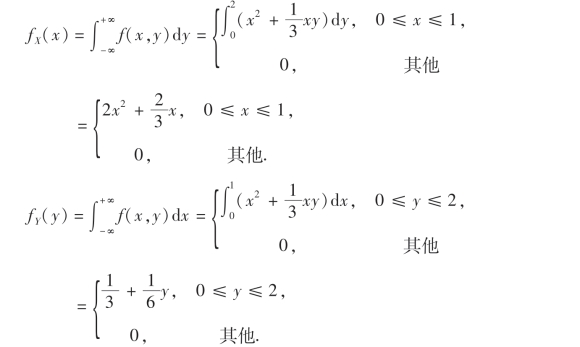
边缘分布函数可由联合分布函数唯一确定，反之结论是否成立呢？下面我们先看一个例子.
例7 设（X，Y）服从二维正态分布，其概率密度为
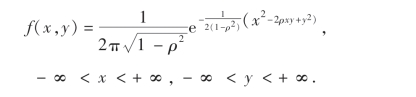
求关于X及关于Y的边缘概率密度.
解 由（3.12）式，得
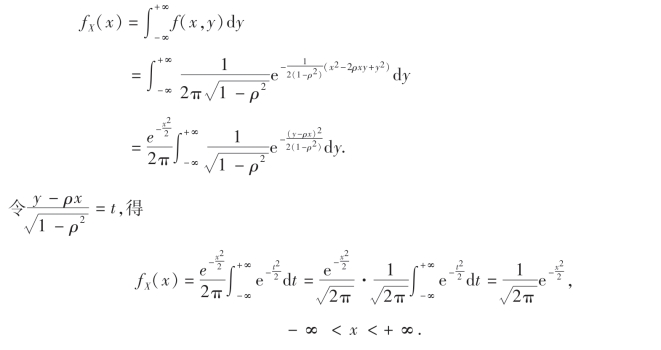
可见X ～N（0，1）.
同理可得关于Y的边缘概率密度
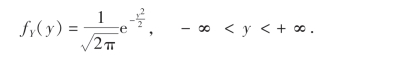
即Y～N（0，1）.
一般地，若（X，Y）～N（μ1，μ2，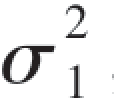
，
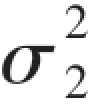，ρ），可以证明X～N（μ1，
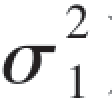），Y～N（μ2，
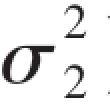）.这就说明二维正态随机变量（X，Y）的两个边缘分布都不依赖于参数ρ.由于不同的ρ对应不同的二维正态分布，因而由（X，Y）的边缘分布不能确定它们的联合分布.这就是说，二维随机变量（X，Y）的性质并不能由它的两个随机变量X与Y的单个性质来确定，还必须考虑它们之间的联系，这正说明了从整体上研究多维随机变量的必要性.