二维随机变量及其分布

一、二维随机变量及其分布

定义1 设E是一个随机试验，它的样本空间是Ω=｛ω｝，设X=X（ω）与Y=Y（ω）是定义在Ω上的两个随机变量，由它们构成的一个向量（X，Y）叫作二维随机变量或二维随机向量.

二维随机变量（X，Y）的性质不仅与X及Y有关，而且还依赖于这两个随机变量的相互关系.因此，逐个地研究X或Y的性质是不够的，还需将（X，Y）作为一个整体来进行研究.

和一维的情况类似，我们引入以下概念.

定义2 设（X，Y）是二维随机变量，对于任意实数x，y，二元函数

称为二维随机变量（X，Y）的分布函数，或称为随机变量X和Y的联合分布函数.

如果将二维随机变量（X，Y）看成是平面上随机点的坐标，那么，分布函数F（x，y）在（x，y）处的函数值就是随机点（X，Y）落在如图3-1所示区域D的概率.

依照上述解释，借助于图3-2容易算出随机点（X，Y）落在矩形域［x1＜x≤x2；y1＜y≤y2］的概率为

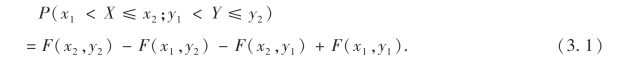
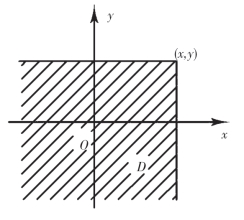
图3-1

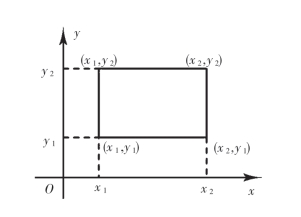
图3-2

分布函数F（x，y）具有以下基本性质：

（1）F（x，y）分别对x和y单调不减，即对于任意固定的y，当x2＞x1时，F（x2，y）≥F（x1，y）；对于任意固定的x，当y2＞y1时，F（x，y2）≥F（x，y1）.

（2）0≤F（x，y）≤1，且

对于任意固定的y，F（-∞，y）=0，

对于任意固定的x，F（x，-∞）=0，

（3）F（x，y）关于变量x或y右连续，即

（4）对于任意的（x1，y1），（x2，y2），x1＜x2，y1＜y2，有下述不等式成立：

性质（1）可由概率的性质证明，性质（2）可由F（x，y）的几何解释加以说明，性质（3）证略，性质（4）由（3.1）式及概率的非负性即可得到.