习题三
1.一枚硬币连掷3次,以X表示在3次中出现正面的次数,以Y表示3次中出现正面次数与反面次数之差的绝对值,试求出(X,Y)的分布律.
2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X表示取到黑球的只数,以Y表示取到红球的只数,求(X,Y)的分布律.
3.随机变量(X,Y)的分布律为
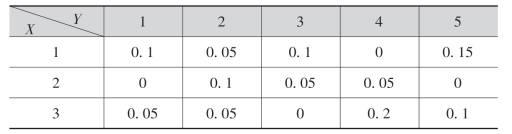
求:(1)P(X <3);
(2)P(Y=2X).
4.随机变量(X,Y)的概率密度为
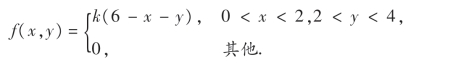
(1)确定常数k;
(2)P(X <1,Y<3);
(3)求P(X <1.5);
(4)求P(X+Y≤4).
5.设随机变量(X,Y)的概率密度为
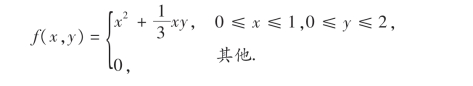
求:(1)(X,Y)的分布函数;
![]()
6.二维随机变量(X,Y)的分布函数为
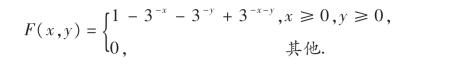
求(X,Y)的概率密度.

8.设二维随机变量(X,Y)的概率密度为
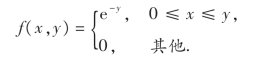
求(X,Y)关于X和关于Y的边缘概率密度.
9.设二维随机变量(X,Y)的概率密度为
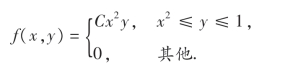
(1)试确定常数C; (2)求边缘概率密度.
10.设二维随机变量(X,Y)的分布律为
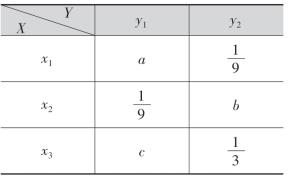
若X与Y相互独立,则a,b,c的值各是多少?
11.设二维随机变量(X,Y)的概率密度为
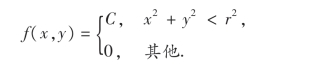
求常数C和边缘概率密度,并确定X和Y的相互独立性.
12.设X,Y是两个相互独立的随机变量,它们均匀地分布在(0,b)内,试求方程t2+Xt+Y=0有实根的概率.
13.设二维随机变量(X,Y)的分布律为
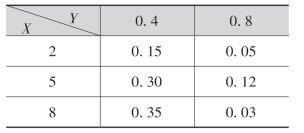
求:(1)在Y=0.4条件下随机变量X的条件分布律;
(2)在X=5条件下随机变量Y的条件分布律.
14.已知(X,Y)的概率密度为
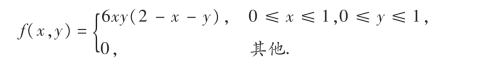
(1)求fX|Y(x|y),fY|X(y|x); (2)问X与Y是否相互独立?
15.设随机变量(X,Y)的概率密度为
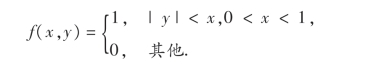
求:(1)fX|Y(x|y),fY|X(y|x);
![]()
16.设随机变量(X,Y)的分布律为
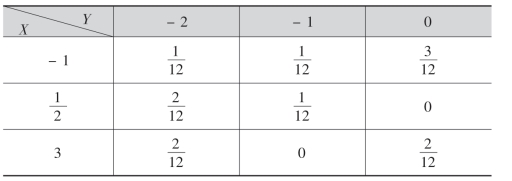
求:(1)(X+Y)的分布律; (2)X2+Y-2的分布律;
![]()
17.设随机变量X与Y相互独立,其概率密度分别为
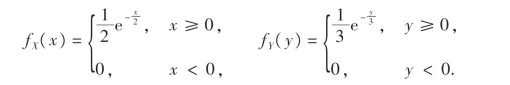
求Z=X+Y的概率密度.
18.设X与Y是相互独立的随机变量,且都服从区间(0,a)上的均匀分布,求Z= 的概率密度.
的概率密度.
19.设随机变量(X,Y)的分布律为
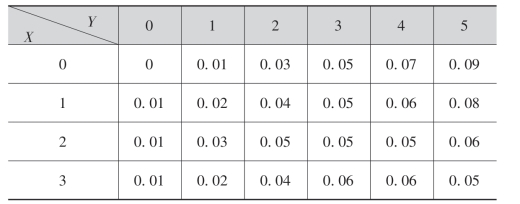
求:(1)Z=min(X,Y)的分布律;
(2)Z=X+Y的分布律;
(3)P(Y=2|X=2).
