一、概率纸法
概率纸法是一种判断总体分布的直观和简便的检验方法，它适合于在现场使用，既可以很快地判断总体分布的类型，又能粗略地估计总体的数字特征.概率纸的种类很多，目前常见的有正态概率纸、对数正态概率纸、二项分布概率纸、指数分布概率纸和威布尔分布概率纸等.在此我们仅介绍正态概率纸，其他类型概率纸使用方法类似，可参照使用.
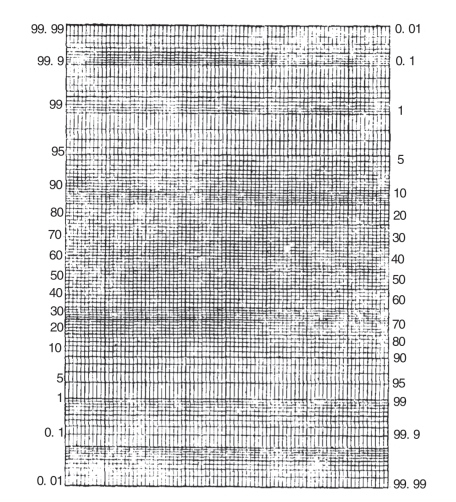
图8-1 正态概率纸
正态概率纸的式样如图8-1所示，事先由厂家印好，我们直接使用.当然我们也可以自己制作，方法是用一张刻有直角坐标的图纸，横坐标轴有均匀刻度，代表观察值，它的纵坐标轴的刻度是不均匀的，表示概率.刻法是：选定各坐标的单位长度，然后按数对（x，Φ（x））来定出纵坐标的刻度，使得标准正态分布函数在此图上的图形恰好是一条直线.在这样的图纸上，即使对于非标准正态分布X ～N（μ，σ2）的分布函数，其图形也是一条直线，这是由于经线性变换
后，非标准正态分布变换为标准正态分布，但直线经线性变换作用保持形状不变.所以只要在横坐标上等间隔地标上x的值，则N（μ，σ2）的分布函数曲线在这张正态概率纸上就是一条直线.
在实践中得知，当n很大时，样本分布函数Fn（x）将近似地等于总体分布函数.于是，根据样本观察值标出点（x，Fn（x））在正态概率纸上的位置，若几乎在同一直线上，我们就可以认为样本来自正态总体.
通过正态概率纸，我们还可以得到μ及σ的近似值.实际上，由于p=0.5，对应于Z=0，从而由
得p=0.5所对应的横坐标就等于μ.同样，p=0.159（或p=0.841）所对应的横坐标就等于μ-σ（或μ+σ）.由此可求出μ及σ的近似值.
下面通过一实例，介绍正态概率图纸的使用方法.
例13 某地区测试了100名12岁儿童的身高，测试数据如下：
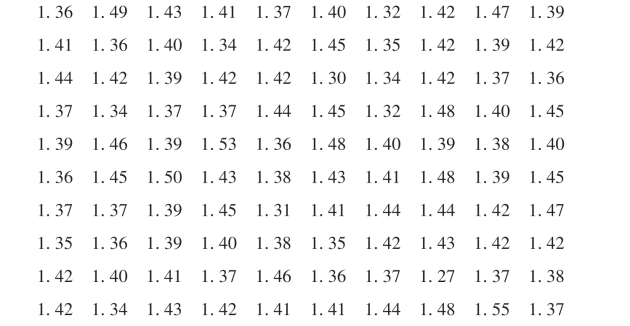
试判断该地区12岁儿童的身高是否服从正态分布.
解 由题意，需检验假设
其中F0（x）为正态分布N（μ，σ2）的分布函数，使用正态概率纸对假设H0做检验时，具体步骤如下：
第一步整理数据.先计算Fn（x），可先将（-∞，x）分为若干个区间，计算出观察值落在这些区间内的频率，累加起来即可得Fn（x），这样得到的值通常称为累积频率.
由于数据较多，把所有点都在正态概率纸上描出显然太烦琐，为简化计算，将这100个数据先从小到大排列，再按等间隔分组，根据经验，当观察值个数多于50时，一般以分为10～25组为宜，并且应使每组至少包含一个数据.注意到数据中最小的为1.27，最大的为1.55.由于读数精度限制，故测得的数据实际上在1.265～1.555之间.因此，分组分点应比读数精度多取一位，且末位取5.今1.555-1.265=0.29，故可取间隔为0.03（称为组距）分组，分为如下10组：
然后统计出各个组内观察值的个数，称为频数，记作ni.这样得到的下表叫频数分布表：
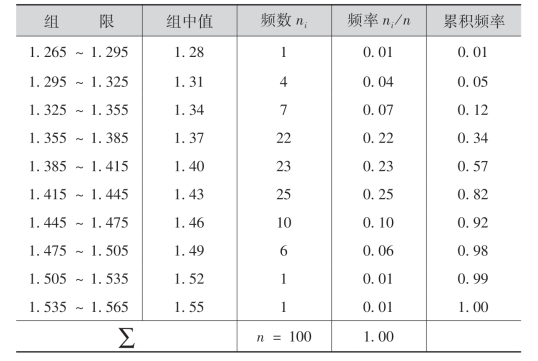
第二步描点.在正态概率纸上描点，横坐标为各组的组上限，纵坐标为表中所对应的累积频率.
于是，先在横坐标上以等间隔标出1.295，1.325，…，1.535各数，再对应纵坐标0.01，0.05，…，0.99，1.00描出各点，如图8-2所示.
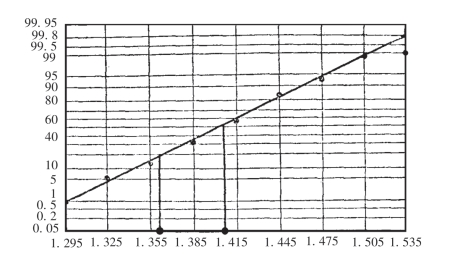
图8-2
第三步直线检验.从图中可以看出这些点近似于一直线，然后用直尺作一直线，使这条直线尽量靠近描的点，本例中除最后一点外，其余各点都与直线很接近.所以我们认为该地区12岁儿童身高服从正态分布.
