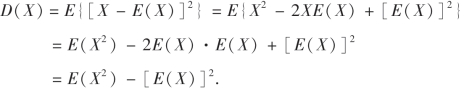一、方差的概念
在上一节中,我们引入了随机变量的数学期望的概念,它反映了随机变量的平均值,是随机变量的重要数字特征.但是在某些场合下只知道平均值是不够的,我们还需要了解随机变量的其他特征.比如,在投资过程中,我们不但要考虑其未来的收益水平,还要考虑其未来收益的不确定性程度,前者可用数学期望来衡量,后者通常称为风险程度,可用收益的波动大小来衡量.下面看一个例子.
例10 某人有一笔资金,想投资房产或购买某种股票,其收益都与市场状态有关,若把未来市场划分为好、中、差三种状态,其发生的概率分别为0.3,0.6,0.1;通过市场调查,该投资者认为,投资房产和购买某种股票在不同的市场状态下其损益值为
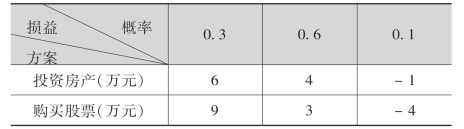
请问:该投资者如何投资为好?
解 设投资房产或购买某种股票的收益分别为随机变量X与Y,则X,Y的数学期望分别为
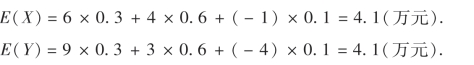
显然,从平均收益看,投资房产和投资股票的收益没有差异,所以有必要考察它们的收益X,Y与平均收益的偏离程度.这时,自然会想到用E{|X-E(X)|}来度量X与其均值E(X)的偏离程度,其中对X-E(X)取绝对值是为了克服其差值的正、负项相抵消,对|X-E(X)|求数学期望是考虑到X对E(X)的平均偏离程度.但由于|X-E(X)|中的绝对值不便处理,故采用E{[X-E(X)]2}代替E{|X-E(X)|}.同理,用E{[YE(Y)]2}代替E{|Y-E(Y)|}.由(4.3)式,得
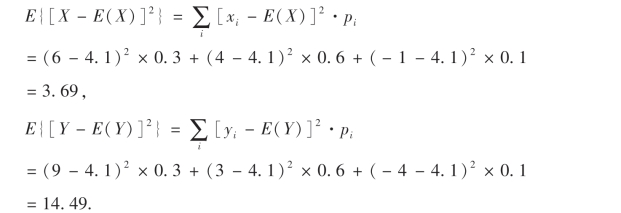
收益的波动愈大,风险也愈大.虽然购买股票与投资房产的平均收益相同,但购买股票比投资房产的风险要大,两者还是选择投资房产为好.由此看出仅根据平均收益来考虑投资是不全面的,还应考虑收益与平均收益的分散程度的大小.那么,如何用数值来反映出随机变量取值的“波动”大小,这是本节要讨论的问题.下面我们引入随机变量方差的概念.
定义3 设X是一个随机变量,若E{[X-E(X)]2}存在,则称E{[X-E(X)]2}为随机变量X的方差,记为D(X)或Var(X),即
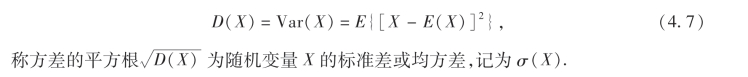
由方差的定义可知方差是一个非负的数,方差与标准差的功能相似,当随机变量X的取值愈集中,则方差与标准差愈小;反之,则方差与标准差愈大.因此方差与标准差都是刻画随机变量X取值的分散程度的一个数字特征.而它们之间的差别主要在量纲上,由于σ(X)与X,E(X)有相同的量纲,所以在实际问题中常被采用.
由定义知,方差实质上就是随机变量X的函数g(X)=[X-E(X)]2的数学期望.
(1)若X为离散型随机变量,其分布律为P(X=xk)=pk,k=1,2,…,则X的方差为
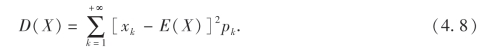
(2)若X为连续型随机变量,其概率密度为f(x),则X的方差为
![]()
随机变量X的方差D(X)通常按下面的公式计算:
![]()
证 由数学期望的性质得