§2.2 离散型随机变量及其分布律
定义3 如果随机变量X只取有限个或可列无限多个不同可能值,则称X为离散型随机变量.
例如,在本章第1节例1中的随机变量只可能取0,1,2三个值,它是一个离散型随机变量;例2中的随机变量,它可能取到的值为0,1,2,3,…,可以一一列举出来,因此也是一个离散型随机变量;例4中的随机变量,它所可能取的值充满区间[0,T],是无法按一定次序一一列举出来,所以它是一个非离散型随机变量.
为了掌握离散型随机变量X的统计规律,必须知道X可能的取值,以及取各个可能值的概率.
定义4 设离散型随机变量X所有可能取的值为x1,x2,…,xi,…,X取可能值xi的概率为pi,即
![]()
则称(2.3)式为离散型随机变量X的分布律或分布列.分布律也常用下述形式表示:

离散型随机变量的分布律具有如下性质:

这两个性质容易利用概率的性质来证明.因为事件的概率是非负的,所以pi=P(X=xi)≥0,即(1)成立.由于x1,x2,…,xi,…是X所取的全部可能值,因此
![]()
注意上式右端各事件两两互不相容,利用概率的可加性得
![]()
即
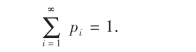
例5 设袋中有3个红球、2个绿球,连续不放回地从袋中取球,直到取得红球为止,设此时取出了X个绿球.试求:
(1)X的分布律;
(2)X的分布函数F(x);
![]()
解 (1)X可能的取值为0,1,2,且
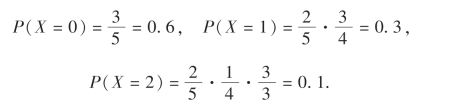
故X的分布律为

(2)当x<0时,{X≤x}为不可能事件,所以
![]()
当0≤x<1时,{X≤x}={X=0},故
![]()
当1≤x<2时,{X≤x}={X=0}∪{X=1},而{X=0}与{X=1}是互不相容的两事件,由概率的有限可加性得
![]()
当x≥2时,{X≤x}为必然事件,所以
![]()
综合即得
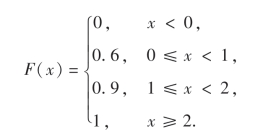
F(x)的图形如图2-1所示,它是一条阶梯形曲线,在x=0,1,2处有跳跃点,跳跃值分别为0.6,0.3,0.1.
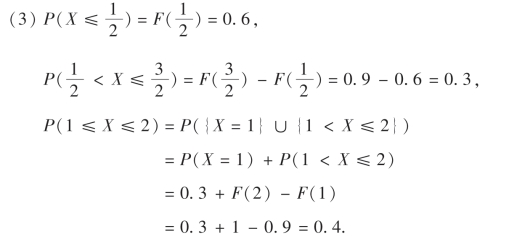
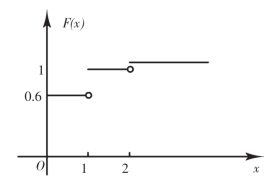
图2-1
一般地,设离散型随机变量X的分布律为
![]()
则X的分布函数为
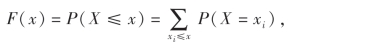
即

其中和式是对所有满足xi≤x的i求和.分布函数F(x)在x=xi(i=1,2,…)处有跳跃,其跳跃值为pi=P(X=xi).
下面介绍几种常见的离散型分布.
1.(0-1)分布
若随机变量X只可能取0与1两个值,它的分布律是
![]()
其中0<p<1.则称X服从(0-1)分布.
考虑本章第1节例3引入的随机变量X,如果掷出正面的概率为p,即P(X=1)=p(0<p<1),则X服从(0-1)分布.显然X的分布函数为
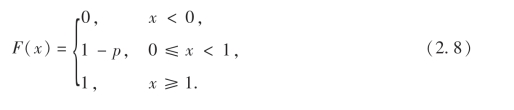
2.二项分布
若随机变量X所有可能的取值为0,1,2,…,n,而取各值的概率为
![]()
其中0<p<1,p+q=1.则称X服从参数为n,p的二项分布,常用记号X~B(n,p)表示.n

在n重贝努里试验中,设每次试验事件A发生的概率为p,令X是n次试验中事件A发生的次数,则X为一离散型随机变量且X ~B(n,p).
顺便指出,(0-1)分布可看作n=1时的二项分布.
例6 设有15台机床独立地各加工一件齿轮,若各机床加工的废品率都是0.4,试求加工出来的15件齿轮中恰有k件(k=0,1,…,15)废品的概率.
解 此例可看作n=15的贝努里试验问题.设X表示加工出来的15件齿轮中的废品个数,则X ~B(15,0.4).故所求概率为
![]()
计算结果列于下表.
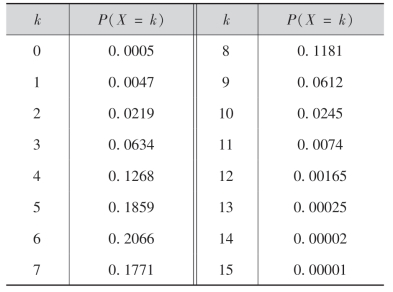
为了对所得的结果有个直观的了解,我们将表中的数据用图形来表示,如图2-2所示.
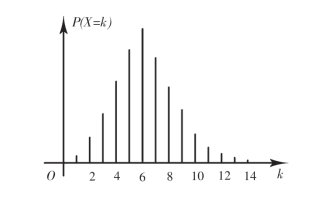
图2-2

证 记λn=npn,则
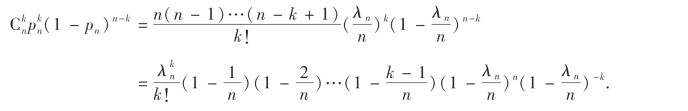
由于对任意固定的k有
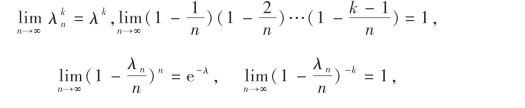
所以
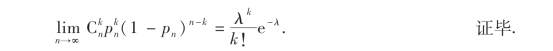
由泊松定理可以看出,当n充分大,p相对很小时,有以下的近似公式
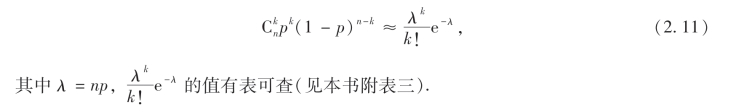
从下表可以直观地看出(2.11)式的近似程度.
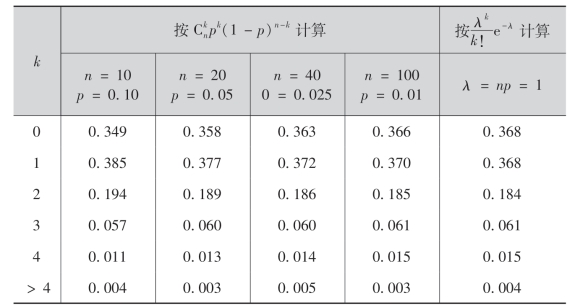
在实际计算中,当n≥50,p≤0.1时,就可以应用公式(2.11).
例7 用步枪向某一目标进行射击,每次击中目标的概率为0.001.现射击6000次,试求至少有两弹击中目标的概率.
解 设X为击中目标的次数,则X ~B(6000,0.001).所求的概率为
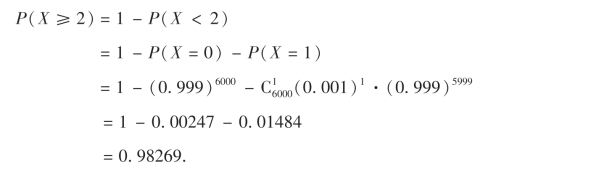
也可用泊松定理做近似计算.这时λ=np=6000×0.001=6.根据公式(2.11)
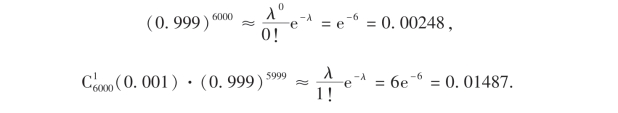
故P(X≥2)≈1-0.00248-0.01487=0.98265.可见近似程度很令人满意.
3.泊松分布
设随机变量X所有可能的取值为0,1,2,…,而取各值的概率为
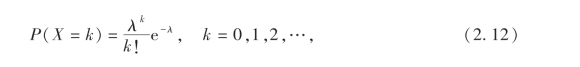
其中λ >0是常数.则称X服从参数为λ的泊松分布,记为X ~π(λ).
容易看出,P(X=k)≥0,k=0,1,2,…,且有
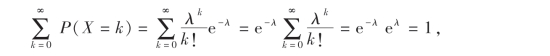
故式(2.12)满足分布律的两个性质.
泊松分布的应用很广泛.例如,在一定时间间隔内某电话交换台收到用户的呼唤次数、一天内到某商店去的顾客数、一定时间内某放射性物质放射的质点数等,都服从泊松分布.
4.几何分布
设随机变量X所有可能的取值为1,2,3,…,而取各值的概率为
![]()
其中0<p<1,q=1-p.则称X服从几何分布,记为X ~G(p).容易验证式(2.13)满足分布律的两个性质.
例8 某流水生产线上每个产品不合格的概率为p(0<p<1),各产品合格与否相互独立,当出现一个不合格产品时即停机检修.设开机后第一次停机时已生产的产品个数为X,试求X的分布律.
解 由题意X的取值为1,2,3,…,k,…,且
P(X=1)=P(开机后生产的第一件产品不合格)=p,
P(X=2)=P(开机后生产的第一件产品合格,但第二件产品不合格)=(1-p)p,
……
P(X=k)=P(开机后生产的前k-1件产品合格,但第k件不合格)=(1-p)k-1p,
……
显然,X服从几何分布.
