一、置信区间
置信区间理论是于1937年由Neyman开始的工作中系统地发展起来的.
参数的区间估计就是求总体未知参数θ的置信度为1-α的置信区间.
置信度1-α反映了区间估计的可靠性，α表示误判风险，区间的长度反映了区间估计的精确度，当区间长度
愈长时，包含真值θ的可能性也就愈大，但估计也愈不精确，甚至失去实际意义.为了提高精度，需将区间定得短些，这时1-α的值较小，可靠性降低.可见可靠性与精确度是相互矛盾的两个侧面，在样本容量n一定时，不能兼顾.因而在实际工作中需结合具体情况全面考虑，充分利用样本提供的信息，做出尽可能可靠和精确的估计.
例13 设X1，X2，…，Xn是来自总体X～N（μ，σ2）的一个样本，σ2＞0为已知参数，μ未知，试求μ的置信度为1-α的置信区间.
解 已经知道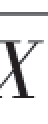
是μ的无偏估计
现α是预先给定的，据标准正态分布的上α分位点zα的定义，有
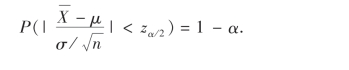
（参见图7-1）
即
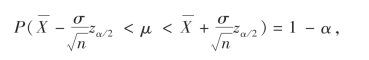
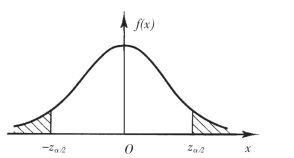
图7-1
所以μ的置信度为1-α的置信区间为
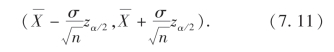
例如，取α=0.05，则1-α=0.95，设σ=1，n=16，¯x=5.20，查表可得zα/2=z0.025=1.96，由（7.11）可得参数μ的置信度为0.95的置信区间为（4.71，5.69），可做这样的解释；若反复抽样多次，每个样本值（n=16）按（7.11）确定一个区间，在这么多的区间中，包含μ的约占95%，不包含μ的约占5%，所得的区间（4.71，5.69）属于那些包含μ的区间的可信程度为95%.
值得注意的是，置信度为1-α的置信区间不是唯一的，对应的区间的长度也可不相同，例如，取α=0.05，把α分位点改成z0.01和z0.04，就有
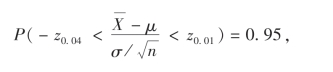
即
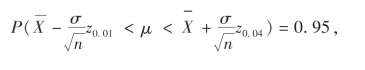
得另一个置信区间为
它的区间长
此式表明区间的长度随n（样本容量）的增加而减少（α给定），所以样本容量越大，区间估计越精确.通过以上的分析，确定未知参数θ的置信区间的一般步骤是：
（1）先求出样本的一个函数：
U包含待估计参数θ，而不含有其他未知参数，U的分布已知且不依赖任何未知参数（当然也不依赖于待估参数θ）.
（2）对于给定的置信度1-α，求出两个常数a，b，使之满足
