三、极大似然法
我们首先看日常生活中的两个例子:发生凶杀案时,破案人员总是把与被害人来往密切又有作案可能性(概率大)的人列为重点嫌疑对象;机器发生故障时,修理工总是从易损部件、薄弱环节开始查起.它们反映的一个事实是:首先想到的是那些使得观测结果出现的可能性最大的情况,也就是说,在获得一些观测资料之后,给参数选取一个数值,使得观测结果出现的可能性最大.这就好比:假定一个随机试验E有若干个可能结果A1,A2,…,An,如果只进行了一次试验,而结果Ai出现了,那么我们有理由相信试验的条件(参数)对“结果Ai出现”是有利,即试验中出现Ai的概率最大.所以当参数未知时,我们应选取参数的估计值,使得试验中出现Ai的概率最大.
极大似然法正是基于这一朴素思想,选取参数的估计值,使得当参数取这一数值时,样本的发生概率最大.
下面通过例子,引进极大似然法.
引例:假定在一个盒子里装有许多黑球和白球,但已知黑球比白球多,我们做有放回的随机抽样,摸球100次,摸到9次白球,试估计黑球和白球的数量之比.
解 在放回的n次随机抽样中,引入随机变量

得到总体X的一个样本X1,X2,…,Xn,可知总体X服从两点分布.
设P(X=1)=p,P(X=0)=1-p=q,0<p,q<1,则有
![]()
据此,事件{X1=x1,X2=x2,…,Xn=xn}发生的概率为
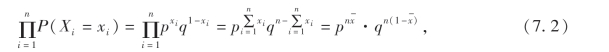
其中xi=0,1(i=1,2,…,n),x1,x2,…,xn是样本X1,X2,…,Xn的一个观察值.
(7.2)式与x1,x2,…,xn和p有关,故设函数

我们把引例中的函数L(x1,x2,…,xn,p)称为似然函数,其一般形式是:若总体X是离散型的随机变量,其分布律为P(X=x)=p(x,θ),其中θ为未知参数,x1,x2,…,xn为样本值,则称乘积
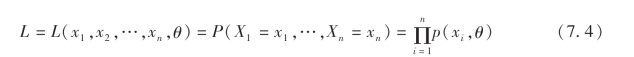
为参数θ的似然函数.
若总体X的概率密度为f(x,θ),可用f(xi,θ)代替概率p(xi,θ),则参数θ的似然函数为
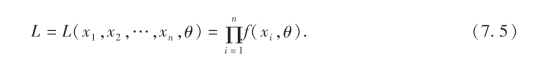
极大似然函数估计法的思想就是:适当地选取θ,使得似然函数L(θ)的值达到最大,也就是使试验得出的结果(样本)X1=x1,X2=x2,…,Xn=xn的概率最大,这个值就是参数θ的估计值.
定义3 假设总体X的分布函数F(x;θ)中含有未知参数θ,X1,…,Xn是总体X的一个样本,x1,x2,…,xn为样本观察值.又假设θ的似然函数为
![]()

例5 设总体X服从参数为θ的指数分布,其概率密度为
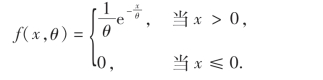
试求参数θ(θ>0)的极大似然估计值.
解 设总体X的一个样本为X1,X2,…,Xn,观察值为x1,x2,…,xn,则参数θ的似然函数是
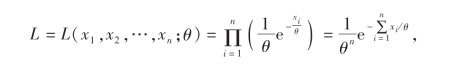
则
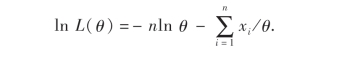
令


例6 设总体X~N(μ,σ2),μ,σ2是未知参数,x1,x2,…,xn是X的一组样本观察值,试求μ,σ2的极大似然估计量.
解 因为X的概率密度是
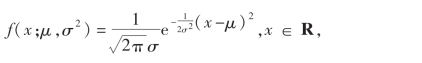
所以似然函数
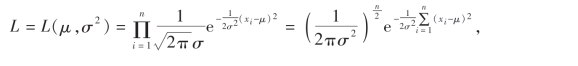
则
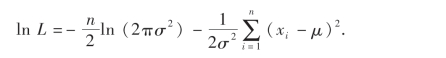
令
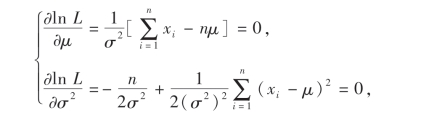
解之可得
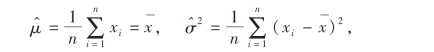
所以μ,σ2的极大似然估计量为

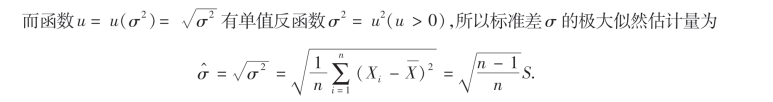
同时,我们还应注意到,有时候不能用似然方程的解得到,而必须用定义来求,请看例7:似然方程有解时,解不一定唯一,此时还要根据二阶导数或其他方法判别是否极大,所以似然函数方程的解不一定都是未知参数的极大似然估计.
例7 设总体X在[θ1,θ2]上服从均匀分布,求θ1,θ2的极大似然估计量.解 因为X的概率密度为
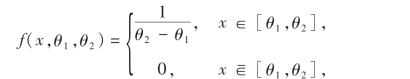
则θ1,θ2的似然函数为
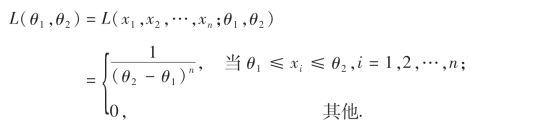
似然方程为

