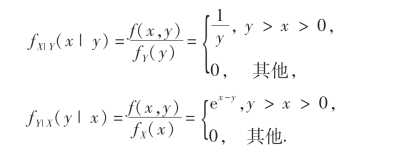* §3.4 条件分布
在第一章中,我们讨论了事件的条件概率,由条件概率很自然引出条件概率分布问题,为此引入
定义6 设(X,Y)是二维离散型随机变量,其分布律为P(X=xi,Y=yj)=pij,i,j=1,2,…;(X,Y)关于X与Y的边缘分布律分别为P(X=xi)=pi·,i=1,2,…;P(Y=yj)=p·j,j=1,2,….
对于固定的j,若P(Y=yj)>0,则称
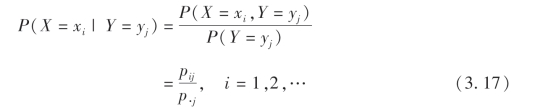
为在Y=yj条件下随机变量X的条件分布律.
同样,对于固定的i,若P(X=xi)>0,则称
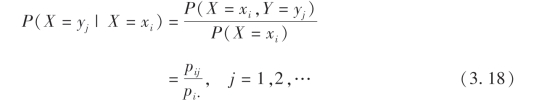
为在X=xi条件下随机变量Y的条件分布律.
容易验证,条件分布律具有分布律的特性:
(1)P(X=xi|Y=yj)≥0;
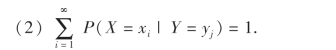
例10 设随机变量(X,Y)的分布律为

求P(X=2|Y=2)及P(Y=2|X=2).
解 由(3.17)及(3.18)式得
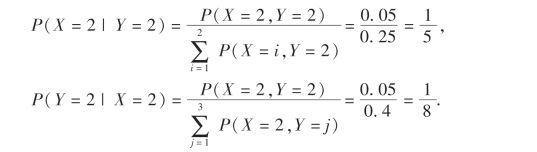
现在来讨论二维连续型随机变量(X,Y)的条件分布,由于对任意x,y都有P(X=x)=0,P(Y=y)=0,因此就不能直接用条件概率公式来定义随机变量的条件分布.下面我们用极限的方法来处理.
定义7 设(X,Y)是二维连续型随机变量,若对于固定的y和Δy>0,P(y<Y≤y+Δy)>0,且极限
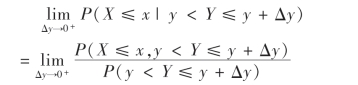
存在,则称此极限为在条件Y=y下X的条件分布函数,记作P(X≤x|Y=y)或FX|Y(x|y).
设(X,Y)的分布函数为F(x,y),概率密度为f(x,y),(X,Y)关于Y的边缘分布函数为FY(y),边缘概率密度为fY(y),且FY(y)>0,则有
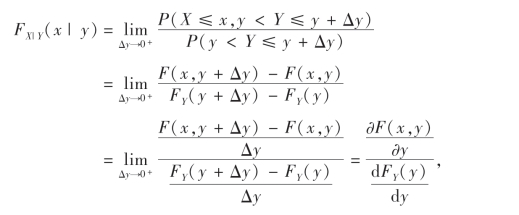
即
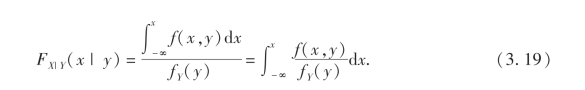
若记fX|Y(x|y)为在条件Y=y下X的条件概率密度,则由(3.19)式知
![]()
类似可以定义FY|X(y|x)和fY|X(y|x),并且当fX(x)>0时,有
![]()
条件概率密度也具有概率密度的性质:
(1)fX|Y(x|y)≥0;
![]()
例11 设随机变量(X,Y)的概率密度为

求fX|Y(x|y)及fY|X(y|x).
解 先求(X,Y)关于X及关于Y的边缘概率密度.
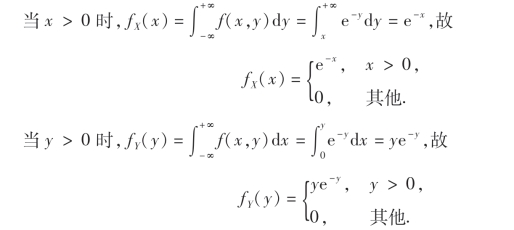
由(3.20)及(3.21)式得