§2.3 连续型随机变量及其概率密度
在上一节我们讨论了离散型随机变量，下面我们将研究另一类重要的随机变量——连续型随机变量.
定义5 设随机变量X的分布函数为F（x），如果存在非负函数f（x），使得对任意实数x有则称X为连续型随机变量，其中函数f（x）称为X的概率密度函数，简称概率密度.
由（2.14）式及微积分的知识可知：连续型随机变量的分布函数F（x）是整个实轴上的连续函数；如果概率密度函数f（x）在x点连续，则F′（x）=f（x）.
连续型随机变量也是在实际应用中经常遇到的一种随机变量.例如，本章第1节例4中的随机变量X，它的分布函数为
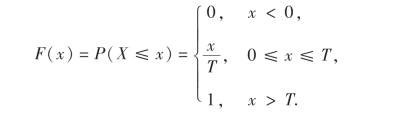
容易验证，对任意的实数x有
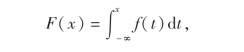
其中
所以X是连续型随机变量.
连续型随机变量X的概率密度f（x）具有如下性质：
（1）f（x）≥0，-∞＜x＜+∞；
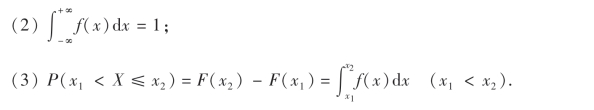
以上性质可分别由概率密度的定义、分布函数的基本性质（2）以及（2.2）式直接得到.性质（1）和性质（2）是概率密度的基本性质.可以证明，满足性质（1）和性质（2）的函数f（x）一定是某一连续型随机变量的概率密度.
由（2.14）式知道.F（x）的值等于以（-∞，x］为底，以曲线y=f（x）为顶的曲边梯形的面积（图2-3）.由性质（2）知道，介于曲线y=f（x）与x轴之间的平面图形的面积为1（图2-4）；由性质（3）知道，X落在区间（a，b］的概率P（a＜x≤b）等于以曲线y=f（x）为曲边、底为区间（a，b］的曲边梯形的面积（图2-5）.
因为在f（x）的连续点x处有f（x）=F′（x），即
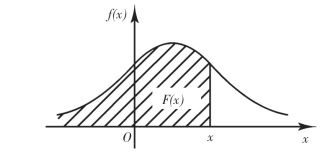
图2-3
图2-4
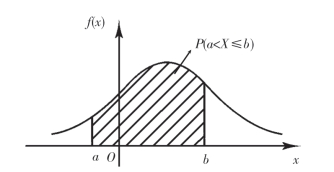
图2-5
所以，若不计高阶无穷小，有
由此可以看出，概率密度f（x）的数值反映了随机变量X取x的邻近值的概率大小.但要注意，连续型随机变量X取单点值的概率为0.事实上，对任一常数a及ε＞0，有
从而
由于连续型随机变量的分布函数是连续函数，所以
即得P（X=a）=0.
由此可见，连续型随机变量与离散型随机变量是有所不同的.对于连续型随机变量，仅知道它取各个可能值的概率还不能掌握它的概率规律，而必须通过它在各个区间的取值的概率才能掌握它的概率规律.另外，我们还可以看出，对于连续型随机变量X来说，事件｛X=a｝并非不可能事件，但有P（X=a）=0.这就是说，若A是不可能事件，则有P（A）=0；反之，若P（A）=0，则A不一定是不可能事件.
由于连续型随机变量取单点值的概率为0，因此，计算连续型随机变量X落在某区间的概率时，区间是否包含端点是无须考虑的.例如有
例9 设连续型随机变量X的概率密度为
（1）确定常数k；
（2）求X的分布函数F（x）；
（2）X的分布函数为
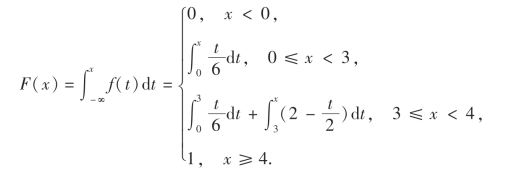
即
例10 设随机变量X的分布函数为
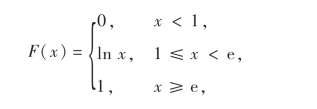
试求X的概率密度.
解 当x＜1或x＞e时，F′（x）=0；
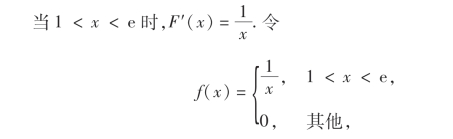
则f（x）为非负函数，且对任意的实数x，有
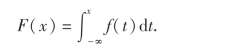
故X为连续型随机变量，其概率密度为f（x）.
当某一随机变量X的分布函数F（x）连续，除有限个点外，导数F′（x）存在并且连续时，则X为连续型随机变量.如果按如下方式作函数f（x）：
（1）在F′（x）存在的点x处，令f（x）=F′（x）；
（2）在F′（x）不存在的点x处，令f（x）为任意非负数.
则f（x）为随机变量X的概率密度.以后在求一个连续型随机变量的概率密度时，除直接使用定义确定外，也常常使用求分布函数导函数的方法.
下面介绍几种常见的连续型分布.
1.均匀分布
设连续型随机变量X具有概率密度
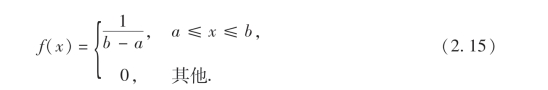
则称X在区间［a，b］上服从均匀分布.
根据（2.15）容易求得X的分布函数为
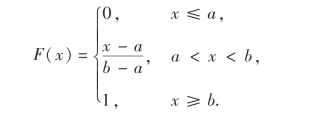
f（x）及F（x）的图形分别如图2-6、图2-7所示.
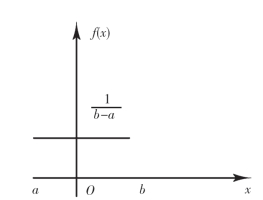
图2-6
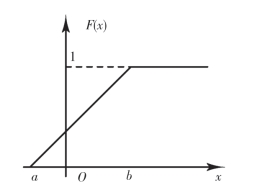
图2-7
若随机变量X在区间［a，b］上服从均匀分布，［c，c+l］为［a，b］的任一子区间，则
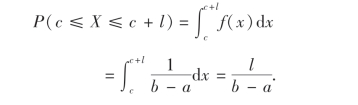
这说明X落在［a，b］的子区间内的概率与子区间的长度成正比，而与子区间的位置无关.可见X落在［a，b］的长度相等的各个子区间的可能性是相等的.
例11 在区间［0，1］上任意投掷一个质点，用X表示这个质点的坐标.设这个质点落在区间［0，1］的任一子区间内的概率与子区间的长度成正比.试求X的分布函数.
解 当x＜0时，｛X≤x｝为不可能事件，所以P（X≤x）=0；
当0≤x≤1时，P（X≤x）表示质点落在区间［0，x］的概率，它与区间［0，x］的长度x成正比，即P（X≤x）=kx.但当x=1时，｛X≤x｝为必然事件，从而P（X≤1）=k·1=1，即k=1，所以P（X≤x）=x；
当x＞1时，｛X≤x｝为必然事件，因此P（X≤x）=1.
于是X的分布函数为
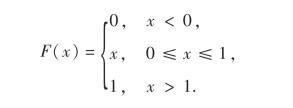
由于F（x）可以表示成下述函数
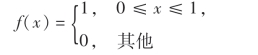
的积分，即
故X在区间［0，1］上服从均匀分布.
2.指数分布
设连续型随机变量X具有概率密度
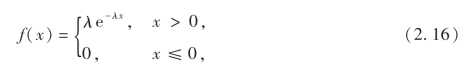
其中λ是正的常数，则称X服从参数为λ的指数分布.
显然f（x）≥0，且
故f（x）满足概率密度的性质（1）和（2）.
由（2.16）式得X的分布函数为
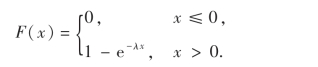
f（x）及F（x）的图形分别如图2-8、图2-9所示.
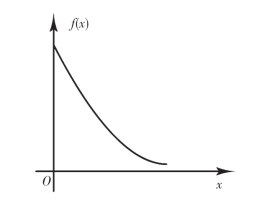
图2-8
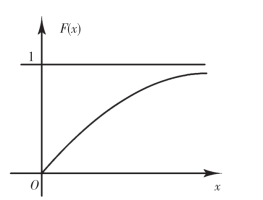
图2-9
指数分布有重要应用，常用它来作为各种“寿命”分布的近似.如电子元件的使用寿命、电话的通话时间等随机变量，都可认为近似地服从指数分布.
例12 某仪器装有3只独立工作的同型号电子元件，其寿命（单位：小时）都服从同一指数分布，概率密度为
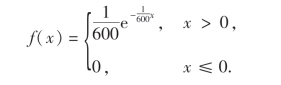
试求在仪器使用的最初200小时内，至少有一只电子元件损坏的概率.
解 以Xi（i=1，2，3）表示第i只元件的寿命，则Xi的概率密度为
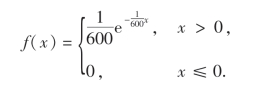
以Ai（i=1，2，3）表示事件“在仪器使用的最初200小时内，第i只元件损坏”，则A1，A2，A3相互独立，且
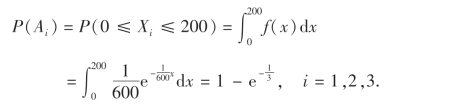
所求概率为
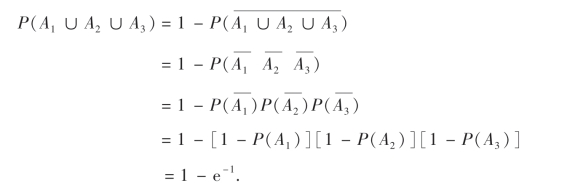
3.正态分布
设连续型随机变量X具有概率密度
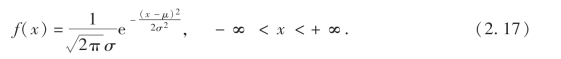
其中μ，σ（σ ＞0）为常数，则称X服从参数为μ，σ的正态分布，记为X ～N（μ，σ2）.
由（2.17）所定义的函数f（x）满足概率密度的两条基本性质.事实上，显然有f（x）＞0，只需验证
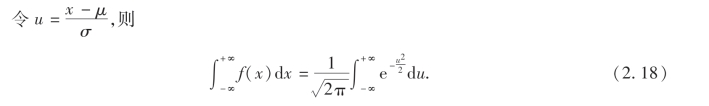
而
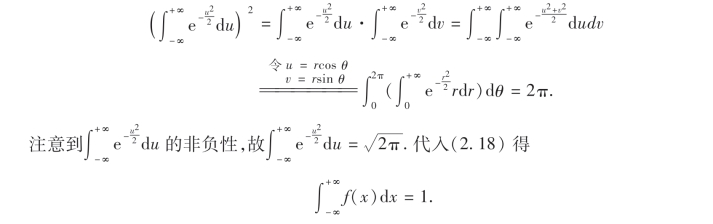
f（x）的图形如图2-10所示，它具有如下性质：
（1）曲线关于x=μ对称.当x=μ时，f（x）取最大值，x离μ越远，f（x）的值越小.因此对任意的h＞0，P（μ-h＜X≤μ）=P（μ＜X≤μ+h），并且对于同样长度的区间，当区间离μ越远，X落在这个区间的概率就越小.
（2）（μ±σ，f（μ±σ））是曲线y=f（x）的拐点.当x→∞时，曲线以x轴为渐近线.
此外，当固定σ值而改变μ值时，f（x）的图形将沿Ox轴平移，而不改变其形状（图2-11）；当固定μ值而改变σ时，由于最大值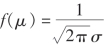
，可见σ越小，f（x）的图形就变得越尖，但对称中心不变（图2-12），因而X落在μ附近的概率越大.
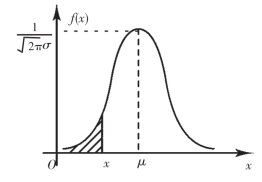
图2-10
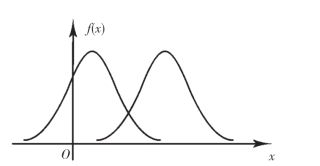
图2-11
由（2.17）式得X的分布函数为
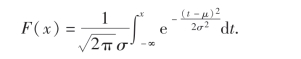
它的图形如图2-13所示.F（x）的值表示图2-10中阴影部分的面积.
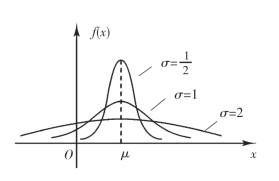
图2-12
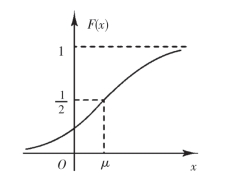
图2-13
特别地，当μ=0，σ=1时，称X服从标准正态分布，其概率密度和分布函数分别用φ（x），Φ（x）表示，即
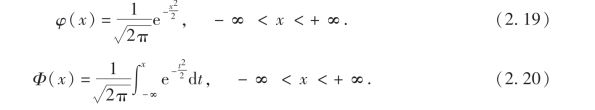
本书末附有标准正态分布函数Φ（x）的数值表，表中列出了对应于x≥0的函数值.利用对称性，可按下面的公式求出对应于x＜0的相应函数值：
一般地，正态分布N（μ，σ2）的分布函数F（x）与标准正态分布N（0，1）的分布函数Φ（x）有如下关系：
这是因为
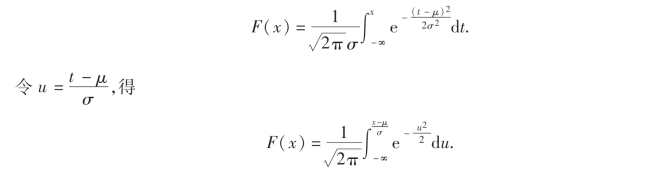
由（2.20），即得（2.22）.
例13 设X ～N（0，1），查表计算：
（1）P（X≤2.2）； （2）P（1.5＜X≤2）；
（3）P（X ＞1.76）； （4）P（X ＜-0.78）；
（5）P（|X|＜1.55）.
其中a＜b.
证 设F（x）为X的分布函数，则
由（2.22）式知故
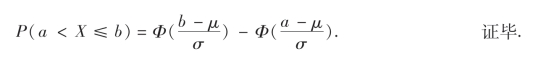
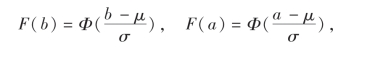
例15 设X ～N（3，22），即μ=3，σ=2，试求：
（1）P（2＜X≤5）； （2）P（-2＜X ＜7）；
（3）P（X ＞3）；（4）P（|X|＞2）.
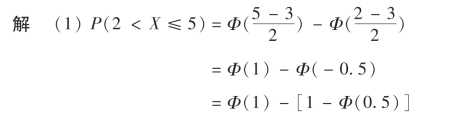
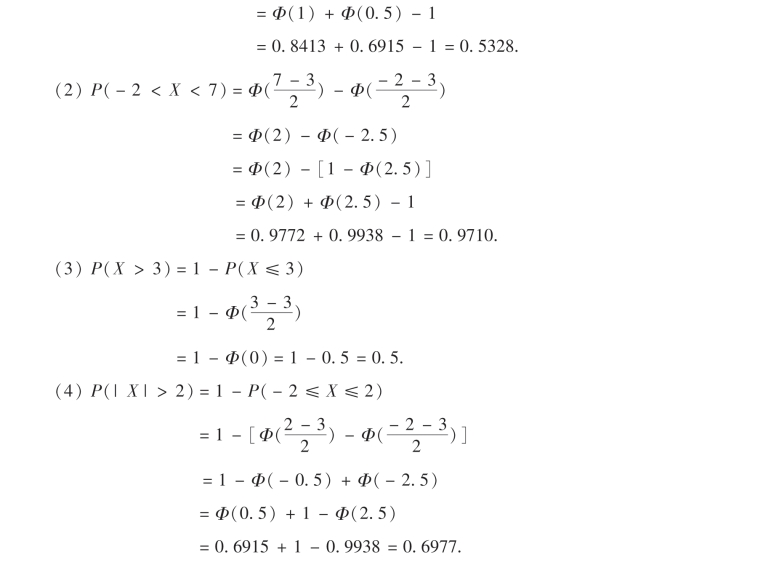
例16 从南郊某地前往北区火车站，可以乘公共汽车，也可以乘地铁.乘汽车所需时间X ～N（50，102），乘地铁所需时间Y～N（60，42）.（单位：分钟）
（1）若有70分钟可用，问乘公共汽车好还是乘地铁好？
（2）若只有65分钟可用，答案又如何？
解 显然，两种走法中以在允许时间内有较大概率及时赶到火车站的走法为好.
（1）有70分钟可用时，乘公共汽车及时赶到火车站的概率为
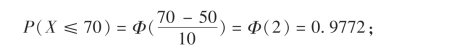
乘地铁及时赶到火车站的概率为
比较即知，应乘地铁较好.
（2）有65分钟可用时，乘公共汽车及时赶到火车站的概率为
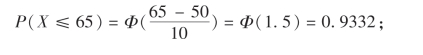
乘地铁及时赶到火车站的概率为
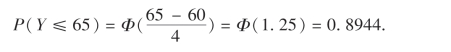
由于前者较大，故乘公共汽车较好.
正态分布是概率论中最重要的一种分布.在实际中，相当广泛一类随机现象都可以用正态分布，或可以近似地用正态分布来刻画.例如，测量某零件长度的测量误差，电子管中的噪声电流或电压，一个地区某种农作物的亩产量等，都服从正态分布.正态分布不仅是具有广泛应用的一种分布，而且在理论上也占有十分重要的地位.在第五章中我们将进一步说明正态分布的重要性.