进度计划优化的方法
进度计划优化的方法有工期优化、费用优化和资源优化三种。优化后的进度计划可以用横道图、时标网络图、里程碑法、进度曲线法(S形曲线)来表示。
(一)工期优化
工期优化是压缩计算工期,以满足工期要求,或在一定条件下使工期最短的过程。工期优化一般通过压缩关键工作的持续时间来进行,其计算步骤如下:
(1)计算网络计划中的时间参数,并找出关键线路和关键工作。
(2)按要求工期计算应缩短的时间ΔT
ΔT=Tc-Tr
式中 Tc——网络计划的计算工期;
Tr——要求工期。
(3)确定各关键工作能缩短的持续时间。
(4)选择应缩短持续时间的关键工作,将其持续时间压至最短,并重新计算网络计划的计算工期和关键线路。若被压缩的工作变成非关键工作,则应延长其持续时间,使之仍为关键工作。选择应缩短持续时间的关键工作时应考虑下列因素:
1)缩短持续时间对质量和安全影响不大的工作。
2)有充足备用资源的工作。
3)缩短持续时间增加费用最少的工作。
(5)若计算工期仍超过要求工期,则重复上述(2)~(4)步骤,直到满足工期要求或工期已不能再缩短为止。
(6)当所有关键工作的持续时间都已达到其能缩短的极限而工期仍不满足要求时,应对计划的原技术、组织方案进行调整或对要求工期重新审定。
【例2-8】 某项目的合同工期为31个月,施工总进度计划如图2-21所示,每项工作可以缩短的时间和因此增加的费用见表2-7。现在业主因为市场原因要求将总工期缩短2个月,问如何调整计划才能满足业主要求同时又使费用增加最少?
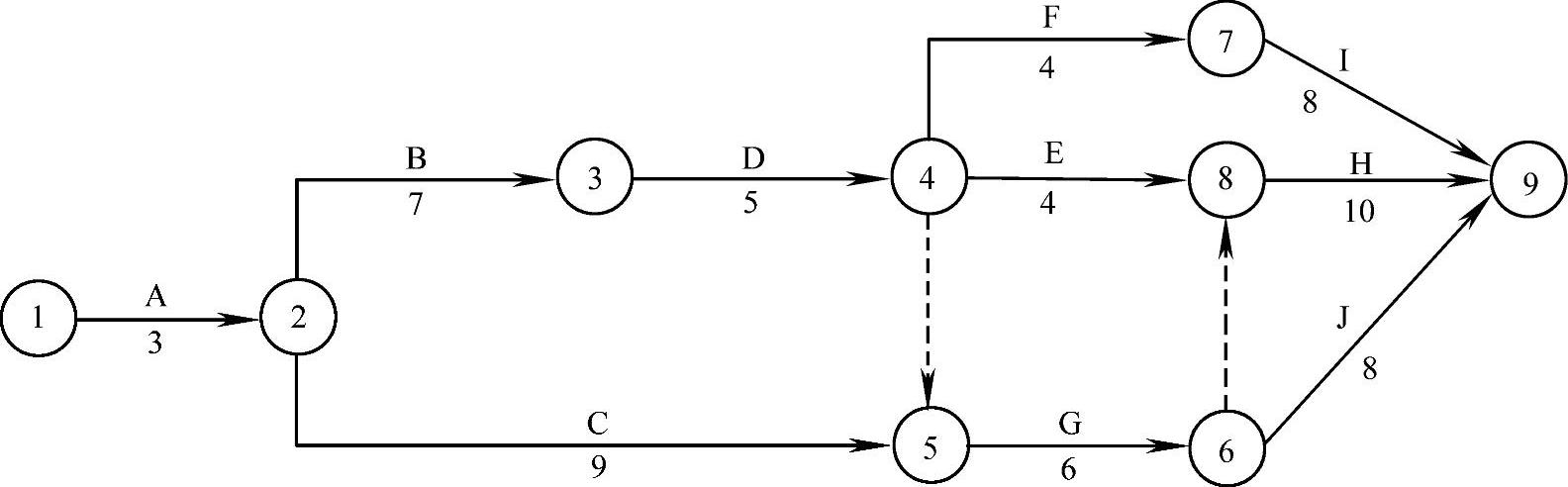
图2-21 初始总进度计划图
表2-7 每项工作可缩短的时间和增加的费用表

【解答】 可按下列步骤进行工期优化:
(1)用标号法确定网络计划的计算工期、关键线路和关键工作,如图2-22所示。关键线路为①—②—③—④—⑤—⑥—⑧—⑨。
(标号法的原理是总持续时间最长的线路为关键线路,方法是在每个节点上标注“该节点计算所得的最早开始时间的来源节点,该节点的最早开始时间”。)
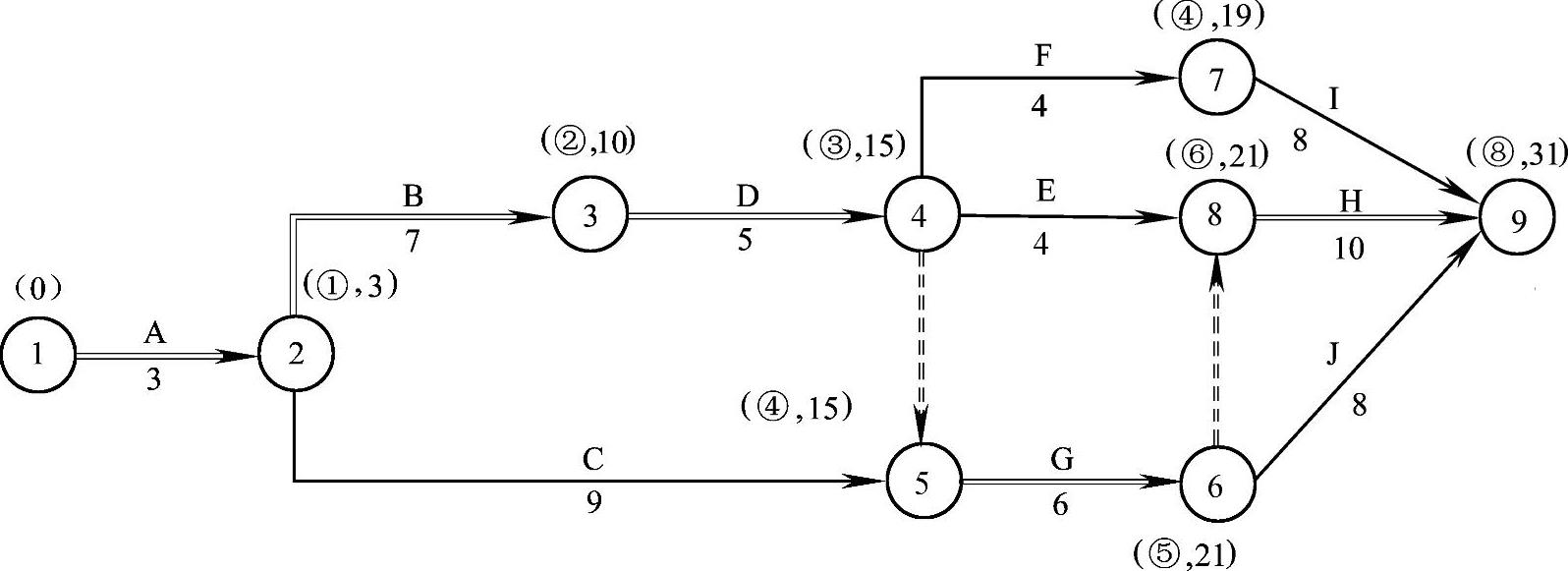
图2-22 初始网络计划中的关键线路
(2)按要求工期应缩短的时间为2个月。
(3)此时关键工作A、B、D、G、H中,工作A没有可缩短的时间,工作G增加的费用最小,所以将工作G作为优先压缩对象。
(4)关键工作G可缩短一个月,此时其持续时间压缩至五个月,利用标号法再确定新的计算工期和关键线路,如图2-23所示;此时关键线路没变。
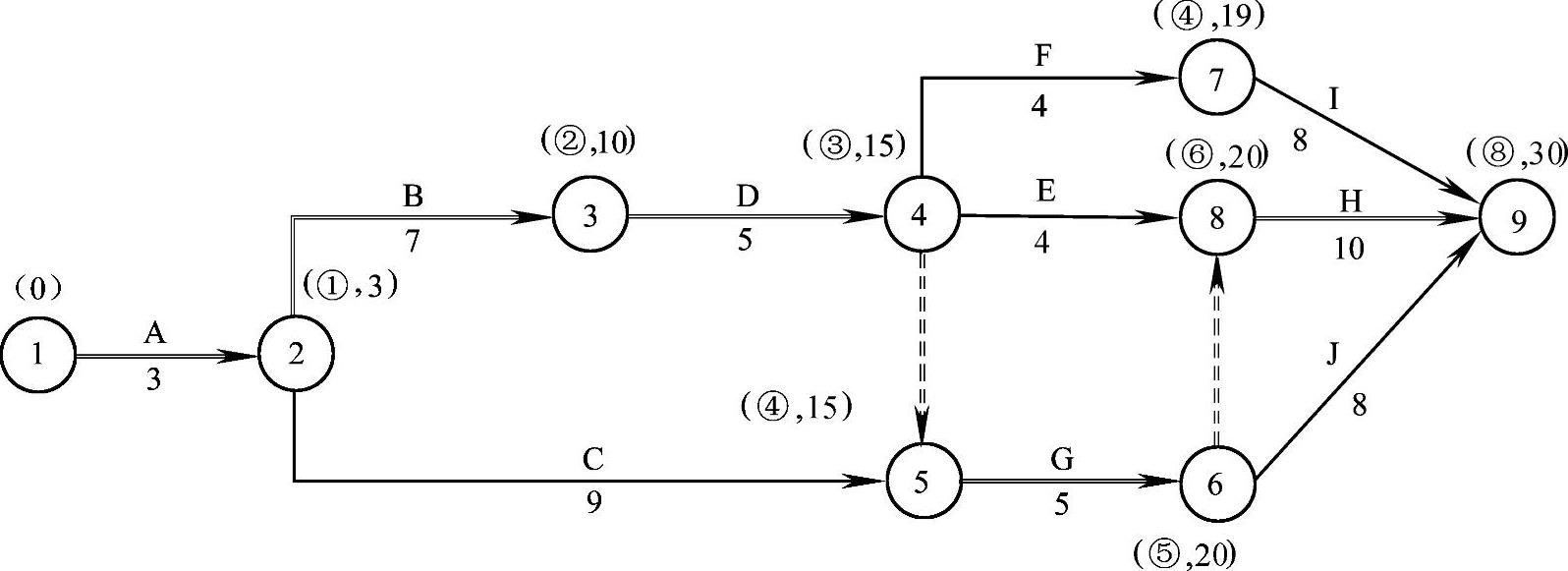
图2-23 第一次压缩后的网络计划
(5)由于要求压缩两个月,而工作G已压缩至极限,所以还有一个月需要压缩;接下来在其他关键工作B、D、H中选择,工作B所增加的费用最小,所以作为压缩对象;工作B的持续时间变为6个月,再用标号法确定计算工期和关键线路,如图2-24所示,关键线路仍未变。
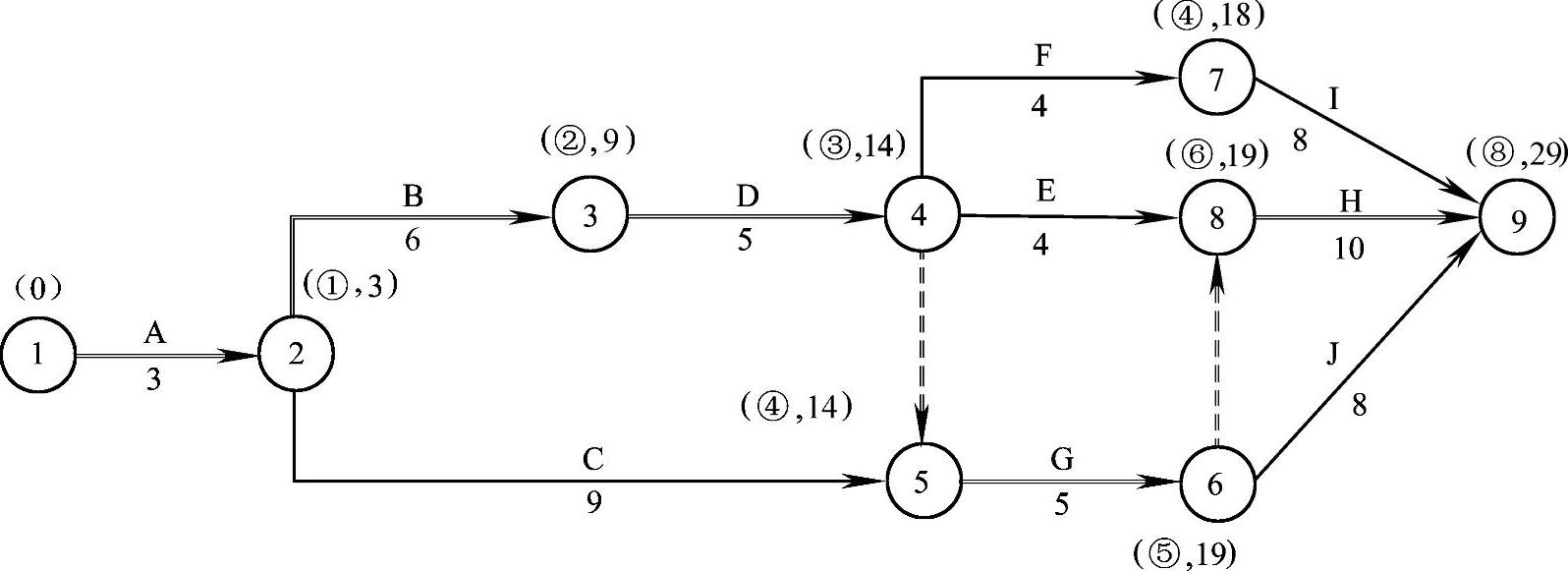
图2-24 第二次压缩后的网络计划
(6)此时,计算工期为29个月,已满足了业主要求,故图2-24所示网络计划即为优化方案。
(二)费用优化
费用优化又叫工期成本优化,是寻求最低成本的最短工期安排,或按要求工期寻求最低成本的计划安排过程。
1.费用优化原理
在进行费用优化时,把工程费用分为两部分。一为直接费,如人工费、材料费、施工机械使用费等。若要缩短工期,可能需夜班工作或在拥挤的工作面上工作,引起工效降低和直接费的增加。二为间接费,例如企业管理费,如果缩短工期间接费将减少。由于两者对于工期长短来说,具有相反的性质,所以总费用如图2-25所示。在总费用曲线中,必定有一个总费用最少的工期,这就是费用优化所寻求的目标,其对应的工期称为最优工期。
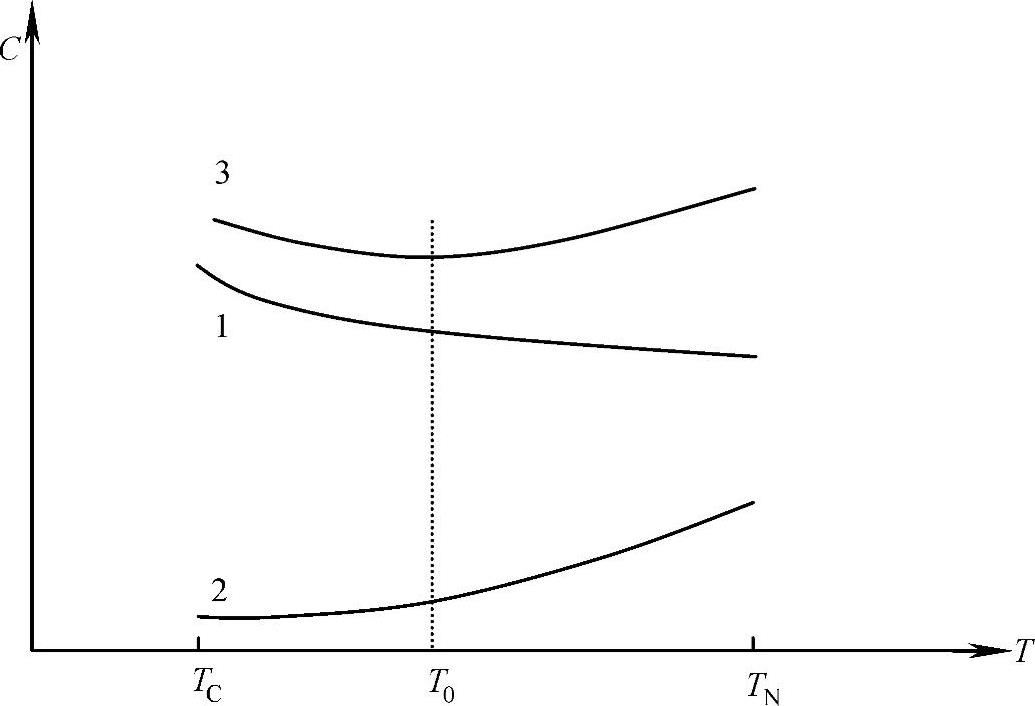
图2-25 工期-费用曲线
1—直接费 2—间接费 3—总费用
TC—最短工期 TN—正常工期 T0—最优工期
基本思路是从网络计划的各工作持续时间和费用的关系中,依次找出能使计划工期缩短而又能使直接费用增加最少的工作,不断地缩短其持续时间,同时考虑其间接费用叠加,即可求出工程总费用最低时的最优工期和工期指定时相应的最低费用。
2.按照上述基本思路,费用优化的步骤:
(1)按工作的正常持续时间确定计算工期和关键线路。
(2)计算各项工作的直接费用率。直接费用率是指一项工作每缩短一个单位时间所需增加的直接费。它等于最短时间直接费和正常时间直接费之差,再除以正常持续时间与最短持续时间之差的商值,即
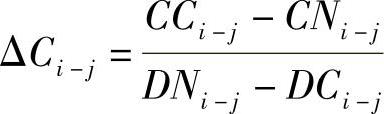
式中 ΔCi-j——工作i-j的直接费用率;
CCi-j——工作i-j持续时间为最短时间时所需的直接费用;
CNi-j——工作i-j持续时间为正常时间时所需的直接费用;
DNi-j——工作i-j的正常持续时间;
DCi-j——工作i-j的最短持续时间。
(3)确定间接费率。间接费用率是指一项工作每缩短一个单位时间所减少的间接费。工作i-j的间接费率表示为ΔCIi-j,它一般都是由各单位根据工作的实际情况而加以确定的。
(4)计算工程总费用。
(5)确定缩短持续时间的关键工作。当只有一条关键线路时,应找出直接费用率最小的一项关键工作,作为缩短持续时间的对象;当有多条关键线路时,应找出组合直接费用率最小的一组关键工作,作为缩短持续时间的对象。
(6)确定持续时间的缩短值。原则是:缩短时间的工作不得变为非关键工作,其持续时间也不能小于其最短持续时间。
(7)计算关键工作持续时间缩短后增加的总费用。
工作持续时间压缩后,工期会相应缩短,项目的直接费会增加,而间接费会减少,所以其总费用应为
Ct=Ct+Δt+Δt[ΔCi-j-ΔCIi-j]
式中 Ct——将工期缩至t时的总费用;
Ct+Δt——工期为t+Δt时的总费用;
Δt——工期缩短值;
ΔCi-j——缩短持续时间工作的直接费用率;
ΔCIi-j——缩短持续时间工作的间接费用率。
(8)重复上述(5)~(6)步骤,直至计算工期满足要求工期或总费用不可降低为止。
(9)计算优化后的工程总费用。
(三)资源优化
资源的供应情况是影响工程进度的主要因素,工程项目中资源包括人力、材料、动力、设备、机具、资金等。因此在编制进度计划时一定要以现有的资源条件为基础,通过改变工作的开始时间,使资源按时间的分布符合优化目标。资源优化包括资源有限—工期最短的优化及工期固定—资源均衡的优化。
1.资源有限—工期最短的优化
资源有限—工期最短的优化是通过调整计划安排以满足资源限制条件并使工期延长最少。其调整步骤如下:
(1)计算网络计划每天资源需用量。
(2)从计划开始日期起,逐日检查每天资源需用量是否超过资源限量,如果在整个工期内每天均能满足资源限量的要求,优化方案就编制完成,否则必须进行计划调整。
(3)调整网络计划。对资源冲突的诸项工作做新的顺序安排。顺序安排的选择标准是工期延长的时间最短;延长的工期等于
ΔTm-n.i-j=EFm-n-LSi-j
式中 ΔTm-n.i-j——将工作i-j安排在工作m-n之后进行时网络计划的工期延长值;
EFm-n——工作m-n的最早完成时间;
LSi-j——工作i-j的最迟开始时间。
(4)重复以上步骤,直至出现优化方案为止。
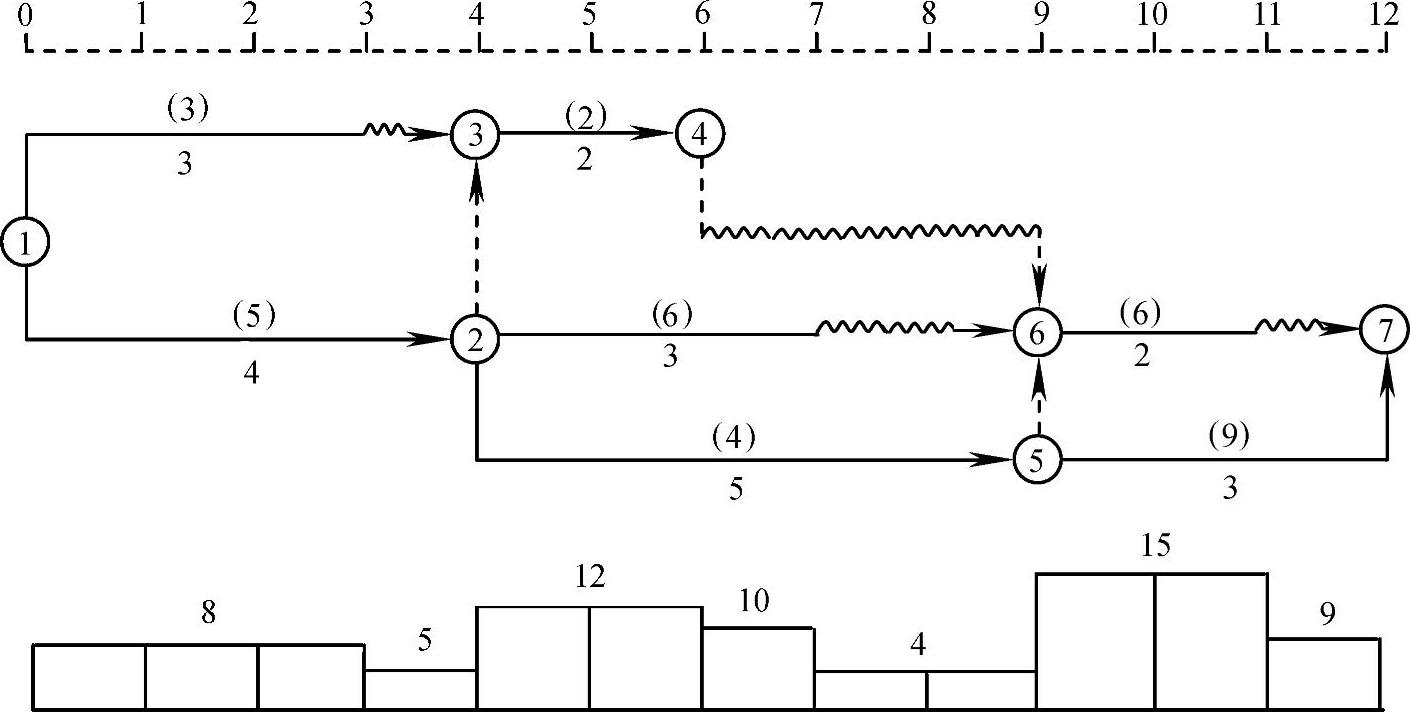
图2-26 双代号时标网络计划
【例2-9】 已知某工程的双代号时标网络计划如图2-26所示,箭线上方数字为初步估算的资金需求量(单位:万元/周),箭线下方数字为每项工作的持续时间(单位:周)。各项工作的时间参数自行计算。由于建设公司资金有限,每周资金运转限量为10万元。试对其进行资源优化,从而达到资金限量要求。
【解答】 根据“资源有限—工期最短”的优化步骤:
(1)计算网络计划每个时间单位的资源需用量,本例中为每周资金需求量,如图2-26下方的直方图曲线所示(费用计划的表示方法之一)。
(2)从计划开始日期起,经检查发现第三时段[4,6]存在资金冲突,资金需要量大于资金限量,需要调整。
(3)时段[4,6]内有工作③—④、工作②—⑤和工作②—⑥平行进行,利用前面的公式计算ΔT值(表2-8)。时间参数按照双代号网络图图上计算法计算,这里简略。
表2-8 延长工期计算表

由表2-9可知,ΔT1,2、ΔT2,1最小,所以1号工作和2号工作谁先谁后都可以,可将2号工作安排在1号工作之后进行,工期不延长。调整后的网络计划如图2-27所示。
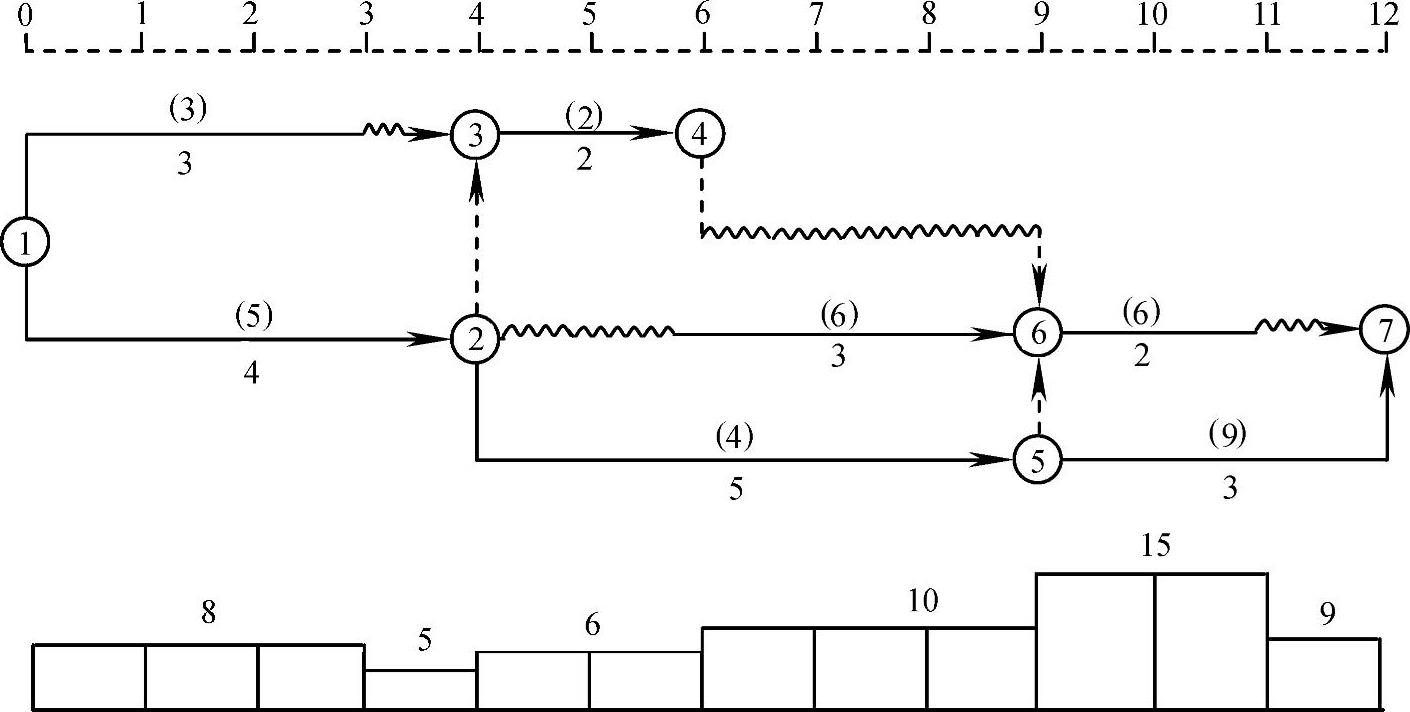
图2-27 第一次调整后的网络计划
(4)第一次调整后的资金需求量动态曲线变成图2-27下方所示,可知第五时段[9,11]存在资金冲突,应调整该时段。
(5)时段[9,11]内有工作⑤—⑦和工作⑥—⑦,按调整后的网络计划计算时间参数,再利用公式计算ΔT值(表2-9)(时间参数计算省略。)
表2-9 延长工期计算表

由表2-9可知,ΔT1,2=ΔT2,1=2,说明两项工作谁先谁后均可。将2号工作安排在1号工作之后,工期延长2周,调整后的网络计划如图2-28所示。
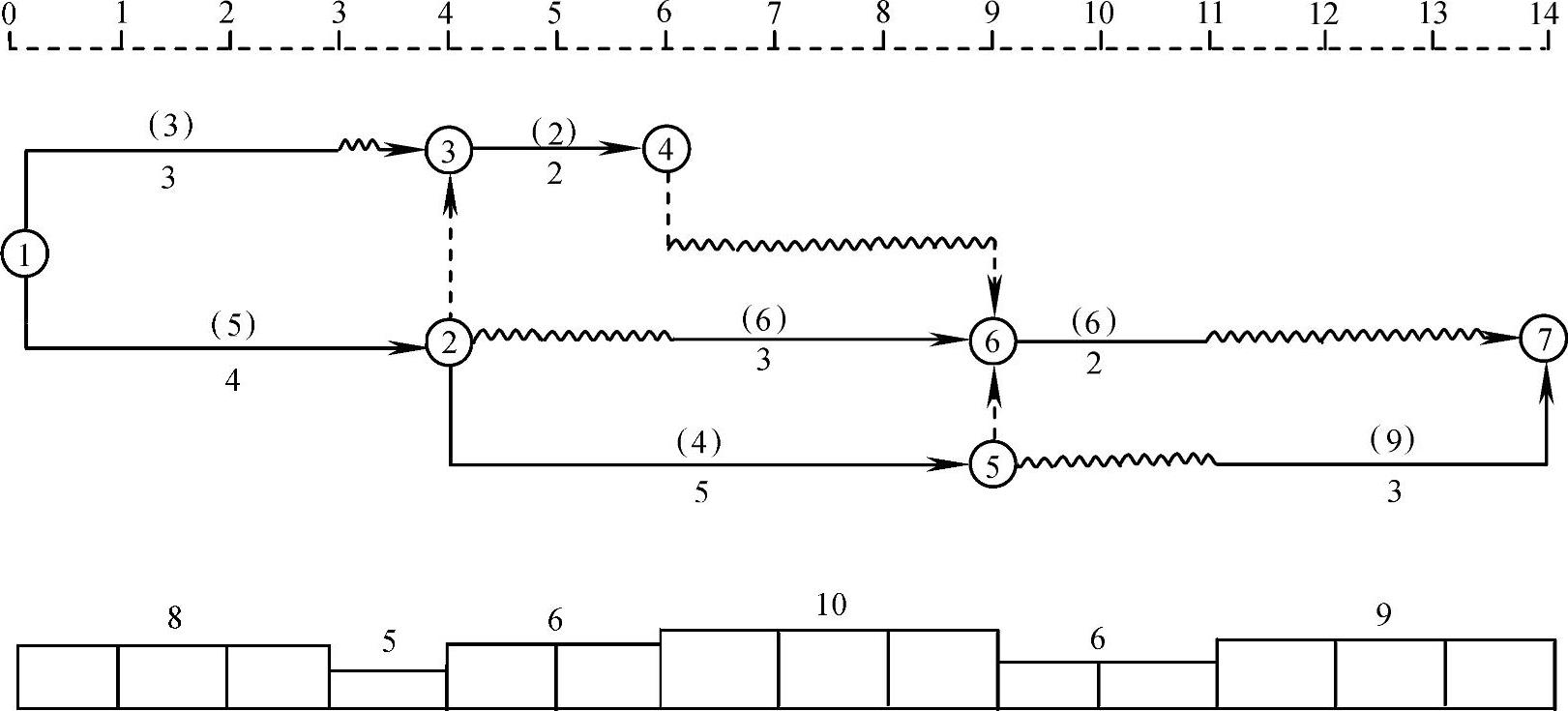
图2-28 优化后的最终网络计划
(6)第二次调整后的网络计划绘成的资金需求量动态曲线如图2-28下方所示,整个工期范围内的资金需求量均未超过资金限量,满足了建设单位的要求。图2-28即为最优方案,其最短工期为14周。
2.工期固定—资源均衡的优化
工期固定—资源均衡的优化是通过调整计划安排,在工期保持不变的条件下使资源需用量尽可能均衡的过程。
1)评价资源均衡性的指标:常用方差(σ2)或标准差(σ)。
方差值越小越均衡。利用方差最小进行网络计划资源均衡优化的基本思路是用初步网络计划所得到的局部时差改善进度计划的安排,使资源动态曲线的方差值减到最小,从而达到均衡的目的。方差和标准差可按下式计算:
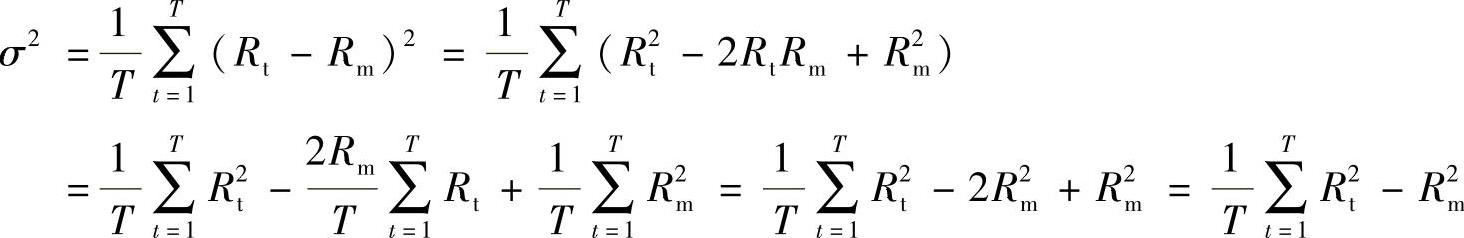
得
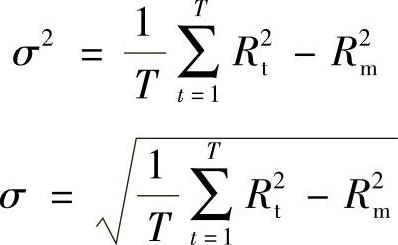
式中 T——规定的工期值;
Rt——瞬时t所需的资源数量;
Rm——日资源需要量的平均值。
因式中规定工期与日资源需要量平均值均为常数,故要使方差值最小,只需使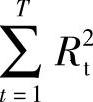 为最小。
为最小。
2)因为工期是固定的,所以求σ2或σ的最小值问题只能在各工作总时差范围内调整其开始和结束时间,从而找出使σ2或σ为最小的优化方案。
