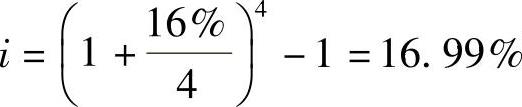资金时间价值与资金等值
(一)资金时间价值的概念
资金在运动过程中随着时间的推移而发生的增值,称为资金的时间价值,主要有两种表现形式:利润和利息。
由于资金存在时间价值,所以不同时点发生的现金流量不能直接进行比较。因此,进行项目经济评价时,首先应对其收益与费用进行时间价值的等值变换,将不同时点上的资金价值转换为相同时点(一个或多个)上的价值,使之具有时间可比性。
(二)资金等值的概念
根据上述资金时间价值等值变换原理,不同时点上的绝对量不等的若干资金,在特定的时间价值(或利率条件)下,可能具有相等的效用或经济价值,这就是资金等值的概念。
影响资金等值的因素有三:①资金额的大小;②换算期数;③利率的高低。
(三)资金时间价值的衡量
利息是资金时间价值的表现形式之一,是指占用资金所付代价或重新使用资金所获报酬。通常用利息额作为衡量资金时间价值的绝对尺度,用利息率(简称为利率)作为衡量资金时间价值的相对尺度。利率通常以一年为期,也有短于一年的。用以表示利率的时间单位称为利息周期(计息期)。
利息=目前应付(应收)总金额-原来借(贷)款金额
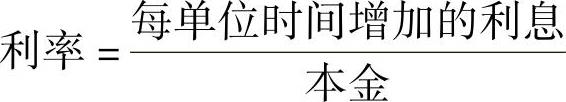
1.单利与复利
(1)所谓单利法 即仅对本金计息,对所获得的利息不再计息。计算公式如下
F=P(1+n×i)
式中 P——本金;
i——期利率;
n——计息次数;
F——本金与利息之和(简称本利和)。
(2)所谓复利法 即不仅本金计息,而且先前周期的利息在后继的周期也要计息。计算公式如下
F=P(1+i)n
【例5-1】 某人以年利率6%借款1000元,预计4年后一次还清全部本金和利息。试分别以单利或复利计息方式计算应偿还额。
【解答】
(1)若计息方式为单利法,则4年后应偿还额:
F=P(1+n×i)=1000×(1+4×6%)=1240元
(2)若计算方式为复利法,则4年后应偿还额:
F=P(1+i)n=1000×(1+6%)4=1262.48元
2.名义利率与有效利率
采用复利计算法,当年计息次数不止一次时,我们把规定的年利率称为名义利率,名义利率除以计息次数为计息期利率,按照复利计算法将计息期利率换算成真正的计息年利率,则为有效利率。换算公式如下
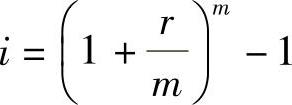
式中 i——有效利率;
r——名义利率;
m——年计息次数。
注意:除了年计息一次时名义利率等于有效利率之外,一年内计息不止一次时,有效利率均大于名义利率。
【例5-2】 若年利率为16%,按季计息,试求有效利率。
【解答】
16%为名义利率r,年计息次数m=4,则