三、无穷小的比较
【主要内容】
1.无穷小的比较
如果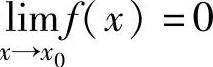
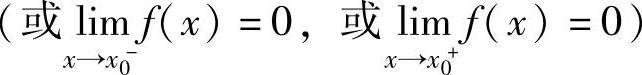 ,则称f(x)是x→x0
,则称f(x)是x→x0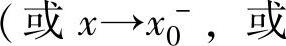
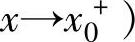 时的无穷小;
时的无穷小;
如果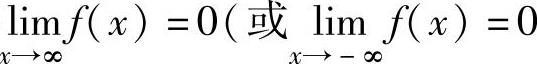 ,或
,或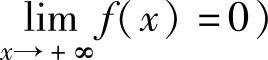 ,则称f(x)是x→∞(或x→-∞或x→+∞)时的无穷小.
,则称f(x)是x→∞(或x→-∞或x→+∞)时的无穷小.
以x→x0的情形为例叙述两个无穷小的比较:
设α(x),β(x)(其中β(x)≠0)都是x→x0时的无穷小.
如果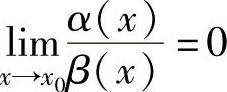 ,则称α(x)是比β(x)高阶的无穷小,记为α(x)=o(β(x));
,则称α(x)是比β(x)高阶的无穷小,记为α(x)=o(β(x));
如果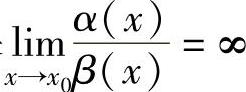 ,则称α(x)是比β(x)低阶的无穷小;
,则称α(x)是比β(x)低阶的无穷小;
如果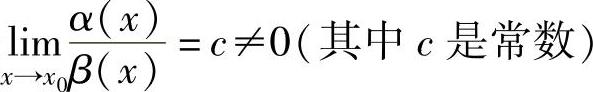 ,则称α(x)与β(x)是同阶无穷小,当β(x)=b(x-x0)k(其中b,k是常数,且b≠0,k>0),称α(x)是k阶无穷小.特别当c=1时,称α(x)与β(x)是等价无穷小,记为α(x)~β(x)(x→x0).
,则称α(x)与β(x)是同阶无穷小,当β(x)=b(x-x0)k(其中b,k是常数,且b≠0,k>0),称α(x)是k阶无穷小.特别当c=1时,称α(x)与β(x)是等价无穷小,记为α(x)~β(x)(x→x0).
2.常用等价无穷小
x→0时,以下的等价无穷小是常用的:
sinx~x,tanx~x,arcsinx~x,arctanx~x,
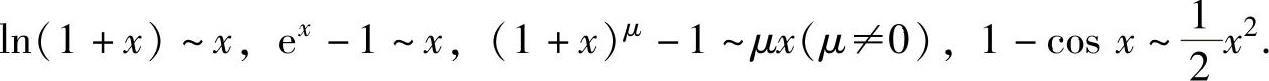
3.等价无穷小代替定理
设x→x0时,无穷小α(x),α1(x),β(x),β1(x)满足α(x)~α1(x),β(x)~β1(x).
如果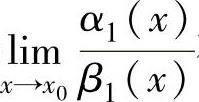 存在或为无穷大,则
存在或为无穷大,则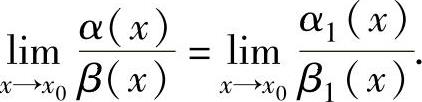
这里的x0若改为x0+,x0-,∞,+∞或-∞,上述结论仍成立.
【典型例题】
例1.3.1 (单项选择题)设当x→0时,(1-cosx)ln(1+x2)是比xsinxn高阶的无穷小,xsinxn是比ex2-1高阶的无穷小,则正整数n为().
A.1B.2C.3D.4
精解 通过寻找x→0时(1-cosx)ln(1+x2),xsinxn及ex2-1的等价无穷小即可算得n的值.
因为当x→0时
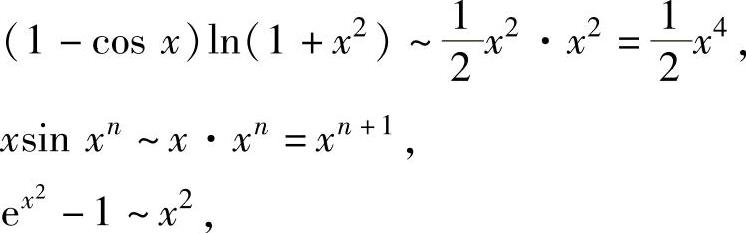 (https://www.daowen.com)
(https://www.daowen.com)
所以,由题设知 4>n+1>2,即n=2,因此选项B是正确的.
例1.3.2 求极限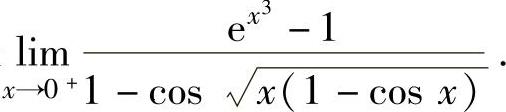
精解 由于x→0+时,
ex3-1~x3,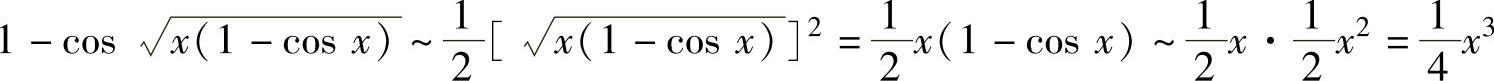 ,
,
所以,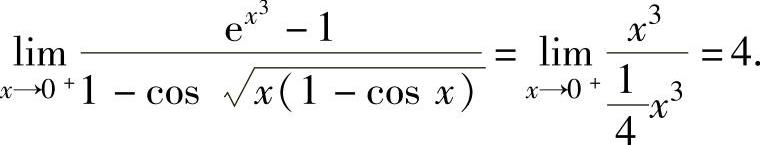
例1.3.3 求极限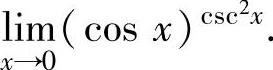
精解 利用公式Ab=eblnA得
(cosx)csc2x=ecsc2xlncosx,
然后计算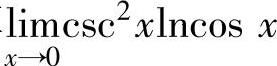 即可.
即可.
由于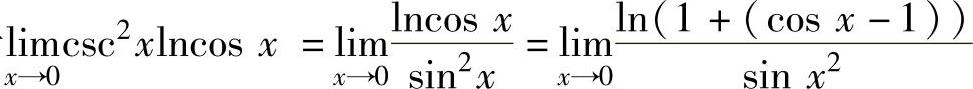
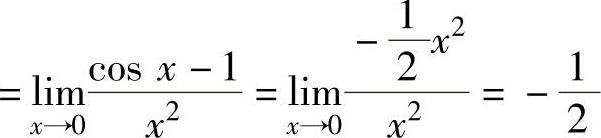 ,
,
所以,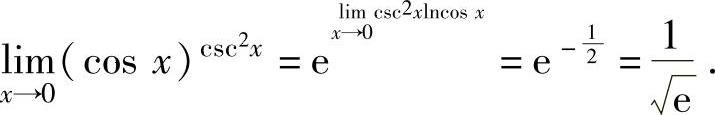 尢
尢
注 应记住公式Ab=eblnA,它可将幂函数转换成指数函数.
例1.3.4 求极限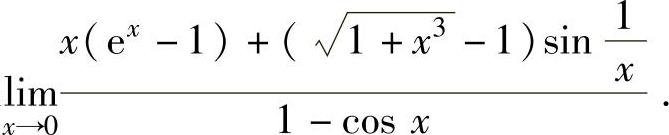
精解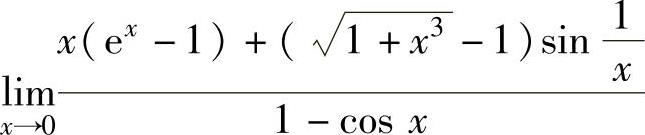
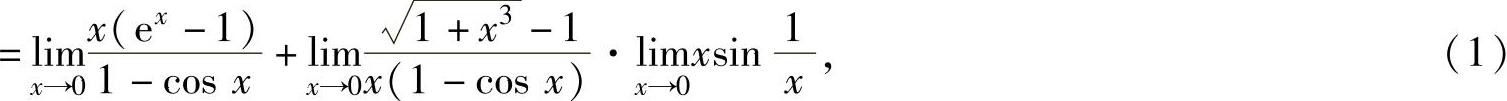
其中,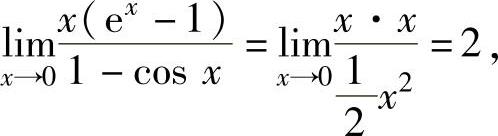
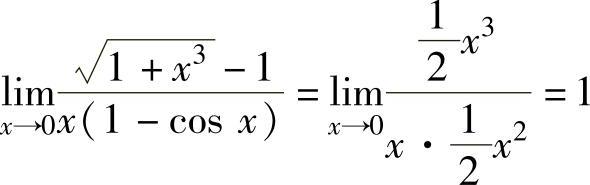 ,
,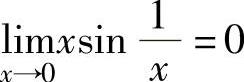 (利用无穷小的性质:设x→x0时,α(x)是无穷小,β(x)在点x0的某个
(利用无穷小的性质:设x→x0时,α(x)是无穷小,β(x)在点x0的某个
去心邻域内有界,则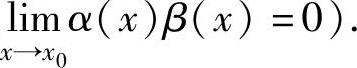
将它们代入式(1)得
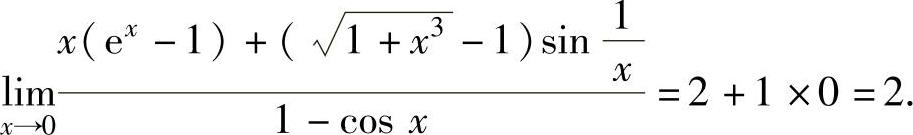
例1.3.5 设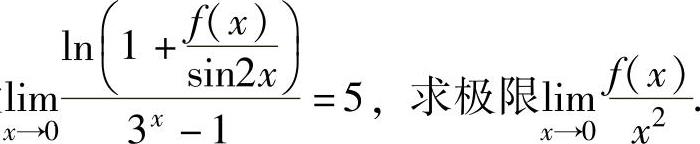
精解 由题设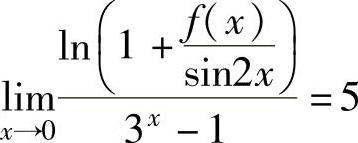 (1)
(1)
得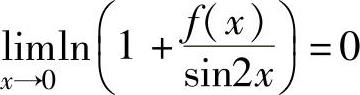 ,即
,即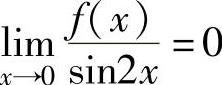 ,并且
,并且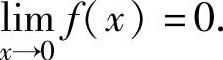
于是由式(1)得
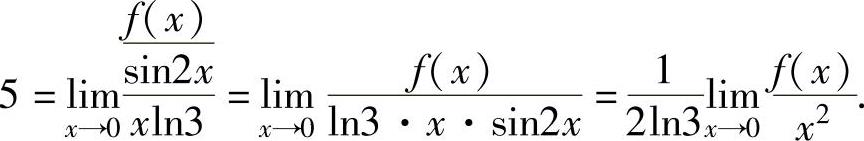
因此,