总体与样本,数理统计中的常用分布
【主要内容】
1.总体与样本
在数理统计中,研究对象的某项数量指标值的全体称为总体,总体可用随机变量描述,该随机变量服从的分布称为总体分布.
设X是总体,如果X1,X2,…,Xn都是与X具有相同分布且互相独立的随机变量,则称X1,X2,…,Xn是来自总体X的容量为n的简单随机样本,简称样本,它的观察值x1,x2,…,xn称为样本值.
如果总体X的分布函数为F(x),则样本X1,X2,…,Xn的联合分布函数为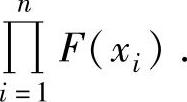 如果总体X是离散型随机变量,其分布律为P(X=xk)=pk(k=1,2,…),则样本X1,X2,…,Xn的联合分布律为P(X1=x1′)P(X2=x2′)…P(Xn=xn′)=p1′p2′…pn′,其中,x1′,x2′,…,xn′∈{x1,x2,…,xn},p1′=P(X1=x1′),p2′=P(X2=x2′),…,pn′=P(Xn=xn′);如果总体X的概率密度为f(x),则样本X1,X2,…,Xn的联合概率密度为
如果总体X是离散型随机变量,其分布律为P(X=xk)=pk(k=1,2,…),则样本X1,X2,…,Xn的联合分布律为P(X1=x1′)P(X2=x2′)…P(Xn=xn′)=p1′p2′…pn′,其中,x1′,x2′,…,xn′∈{x1,x2,…,xn},p1′=P(X1=x1′),p2′=P(X2=x2′),…,pn′=P(Xn=xn′);如果总体X的概率密度为f(x),则样本X1,X2,…,Xn的联合概率密度为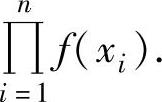
设X1,X2,…,Xn是来自总体X的一个简单随机样本,g(t1,t2,…,tn)是不含总体未知参数的n元函数,则称随机变量T=g(X1,X2,…,Xn)是样本X1,X2,…,Xn的一个统计量,设x1,x2,…,xn是样本X1,X2,…,Xn的观察值,则称函数值g(x1,x2,…,xn)为统计量T的观察值.
2.样本的数字特征
设X1,X2,…,Xn是总体X(EX=μ,DX=σ2)的一个简单随机样本,其观察值为x1,x2,…,xn.
(1)样本均值X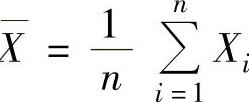
样本均值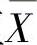 的数学期望
的数学期望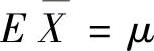 ,方差
,方差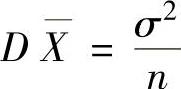 ,且
,且
当X~N(μ,σ2)时,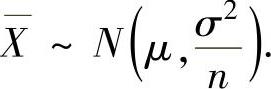
样本均值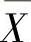 的观察值
的观察值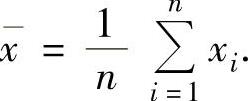
(2)样本方差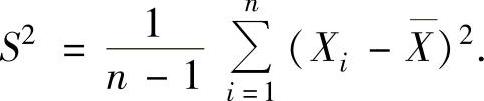
样本方差S2的计算公式: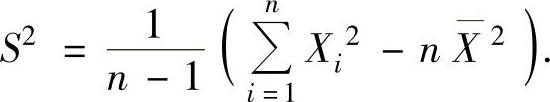
样本方差S2的数学期望ES2=σ2.
样本标准差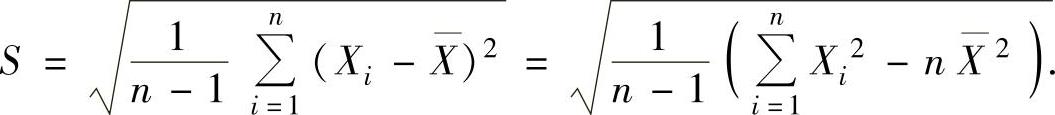
样本方差观察值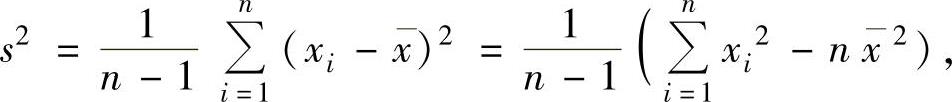
样本标准差观察值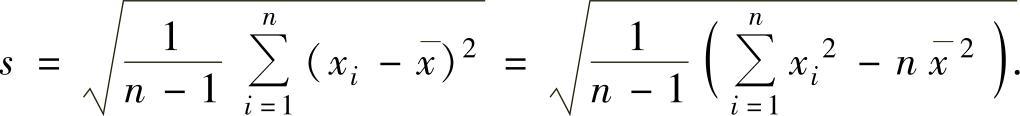
(3)样本k阶原点矩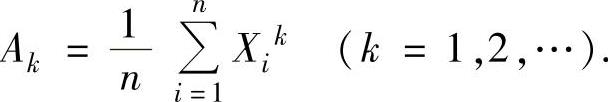
显然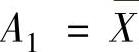 ,
,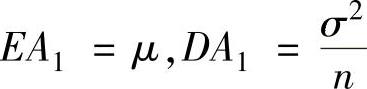 ;
;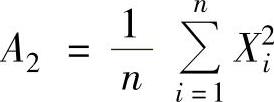 ,EA2=σ2+μ2.
,EA2=σ2+μ2.
样本k阶原点矩观察值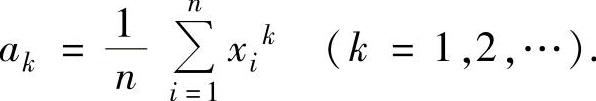
(4)样本k阶中心矩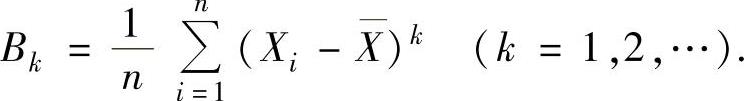
特别称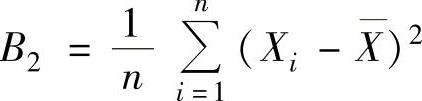
为样本的修正方差,显然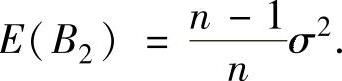
样本k阶中心矩观察值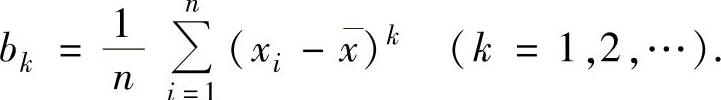
3.数理统计中的常用分布
(1)标准正态分布
参数μ=0,σ2=1的正态分布称为标准正态分布,记为N(0,1).
(ⅰ)设X~N(0,1),则EX=0,DX=1.
(ⅱ)设X~N(0,1),则X的概率密度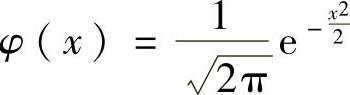 ,分布函数Φ(x)=
,分布函数Φ(x)=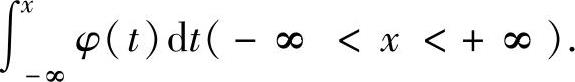 显然,
显然,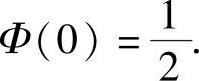
当x<-3时,Φ(x)≈0;当x>3时,Φ(x)≈1.对任意实数x有Φ(-x)=1-Φ(x).
(ⅲ)设X~N(0,1),则对α∈(0,1),称满足P(X>zα)=α的实数zα为标准正态分布的上α分位数,它满足z1-α=-zα.
(2)χ2分布
设X1,X2,…,Xn相互独立,且都服从标准正态分布,则称随机变量X=X12+X22+…+Xn2服从的分布为自由度为n的χ2分布,记为χ2(n).
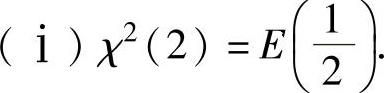
(ⅱ)设随机变量X~χ2(n),则EX=n,DX=2n.
(ⅲ)设随机变量X,Y相互独立,且X~χ2(n1),Y~χ2(n2),则X+Y~χ2(n1+n2).
(ⅳ)设随机变量X~χ2(n),则对α∈(0,1),称满足P(X>χ2α(n))=α的实数χ2α(n)为自由度为n的χ2分布的上α分位数.(https://www.daowen.com)
(3)t分布设随机变量X~N(0,1),Y~χ2(n),并且X与Y相互独立,则称随机变量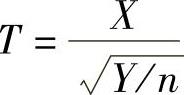 所服从的分布为自由度为n的t分布.
所服从的分布为自由度为n的t分布.
(ⅰ)设T~t(n),则随机变量T的概率密度fn(t)是偶函数;
(ⅱ)设T~t(n),则当n充分大时T~N(0,1).
(ⅲ)设T~t(n),则对α∈(0,1),称满足P(T>tα(n))=α的实数tα(n)为自由度为n的t分布的上α分位数,它满足t1-α(n)=-tα(n).
(4)F分布设随机变量U和V相互独立,且U~χ2(n1),V~χ2(n2),则称随机变量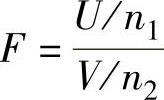 所服
所服
从的分布为自由度为(n1,n2)的F分布,记为F(n1,n2).
(ⅰ)设F~F(n1,n2),则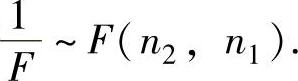
(ⅱ)设F~F(n1,n2),则对α∈(0,1),称满足P(F>Fα(n1,n2))=α的实数Fα(n1,n2)为自由度为(n1,n2)的F分布的上α分位数,它满足
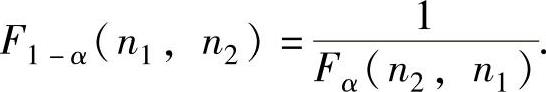
【典型例题】
例8.1.1 (单项选择题)设随机变量X和Y都服从N(0,1),则下列结论中正确的是( ).
A.X+Y服从正态分布
B.X2+Y2服从χ2分布
C.X2和Y2都服从χ2分布
D.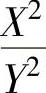 服从F分布
服从F分布
精解 由于X~N(0,1),所以X2~χ2(1),同样Y2~χ2(1),所以X2和Y2都服从χ2分布.
因此本题选C.
注 由于X,Y未必相互独立,所以X+Y也未必服从正态分布,X2+Y2未必服从χ2分
布,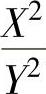 未必服从F分布.
未必服从F分布.
例8.1.2 (单项选择题)设随机变量X~t(n)(n>1),则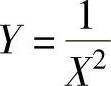 ~( ).
~( ).
A.χ2(n) B.χ2(n-1) C.F(n,1) D.F(1,n)
精解 由于X~t(n),所以由t分布的定义知存在相互独立的随机变量U~N(0,1),V~χ2(n),使得
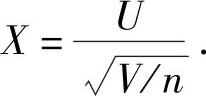
于是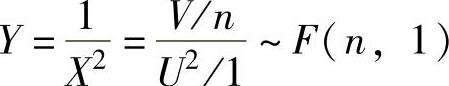 (这是由于V与U2相互独立,V~χ2(n),U2~χ2(1)).因此本题选C.
(这是由于V与U2相互独立,V~χ2(n),U2~χ2(1)).因此本题选C.
例8.1.3 设总体X~π(λ),X1,X2,…,Xn是来自X的一个简单随机样本.
(1)写出X1,X2,…,Xn的联合分布律;
(2)记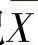
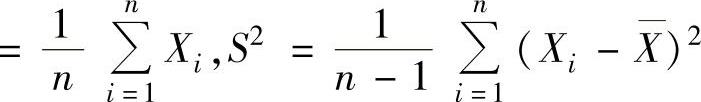 ,求
,求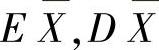 和ES2.
和ES2.
精解 (1)由于X的分布律为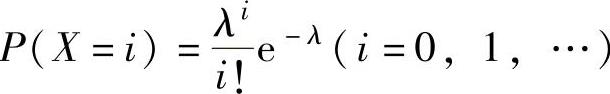 ,所以X的简单随机样
,所以X的简单随机样
本X1,X2,…,Xn的联合分布律为
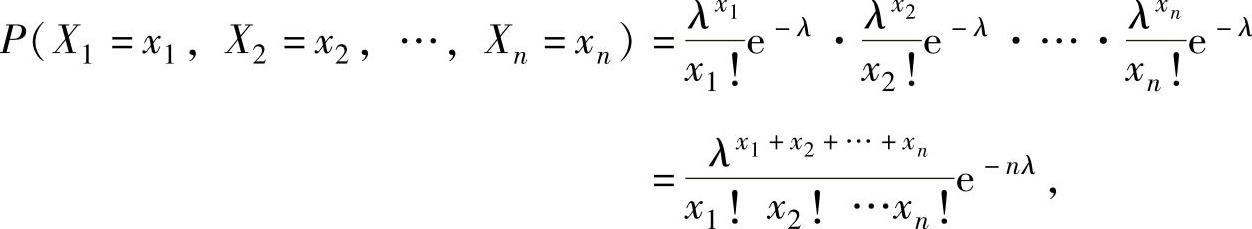
其中,x1,x2,…,xn都是任意的非负整数.
(2)由于总体X的数学期望μ=EX=λ,方差σ2=DX=λ,所以
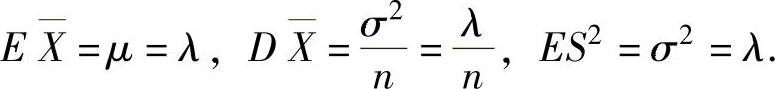
例8.1.4 设X1,X2,…,X9和Y1,Y2,…,Y9分别是来自相互独立总体X~N(0,32)和Y~N(0,32)的简单随机样本,求统计量
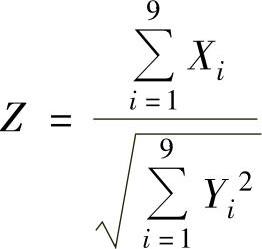
所服从的分布.
精解 由于X1,X2,…,X9是来自总体X~N(0,32)的简单随机样本,所以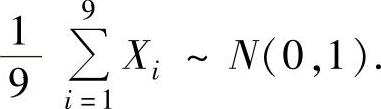
由于Y1,Y2,…,Y9是来自Y~N(0,32)的简单随机样本,所以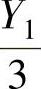 ,
,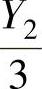 ,…,
,…,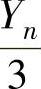 相互独立且都
相互独立且都
服从N(0,1),因此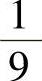
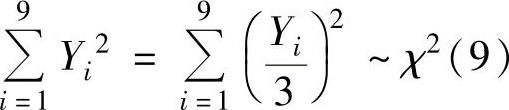 ,此外,
,此外,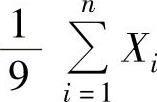 与
与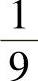
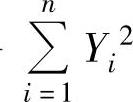 相互独立.于是
相互独立.于是
由t分布的定义知
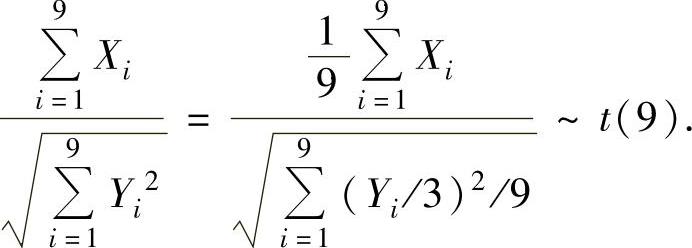
例8.1.5 从总体X~N(3.4,62)中抽取容量为n的简单随机样本,如果要求该样本均值位于区间(1.4,5.4)内的概率不小于0.95,问样本容量n至少取多大?
精解 由题设知样本均值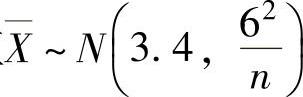 ,所以
,所以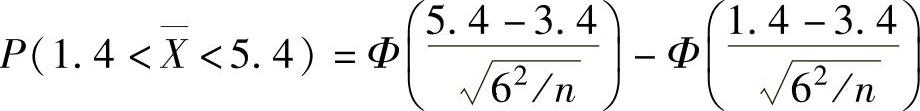 (Φ(x)是标准正态分布函数)
(Φ(x)是标准正态分布函数)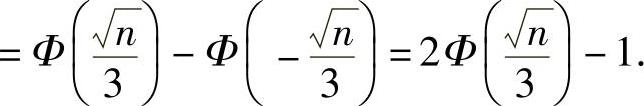
于是由题设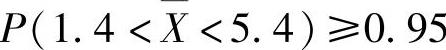 得
得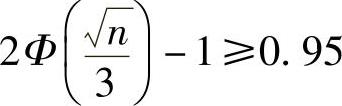 ,即
,即

由于Φ(1.96)=0.975,且Φ(x)是单调增加函数,所以由式(1)得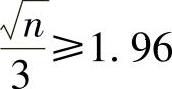 ,即n≥34.57.
,即n≥34.57.
因此,此样本容量至少应为35,才能使样本均值位于区间(1.4,5.4)之内的概率不小于0.95.
例8.1.6 设总体X~N(0,σ2),X1,X2,…,X9是来自X的简单随机样本,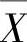 是它的均值.确定σ的值,使得P(1<X<3)为最大.
是它的均值.确定σ的值,使得P(1<X<3)为最大.
精解 由题设知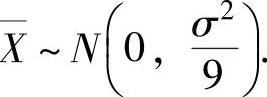 所以
所以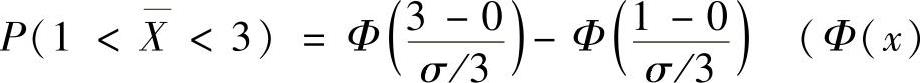 是标准正态分布函数)
是标准正态分布函数)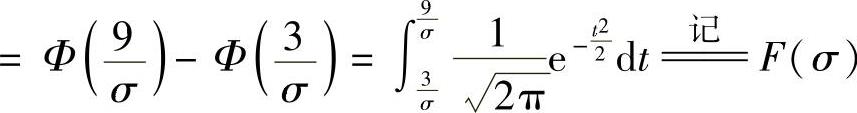 ,
,
则F(σ)的定义域为(0,+∞),在其上可导,且由
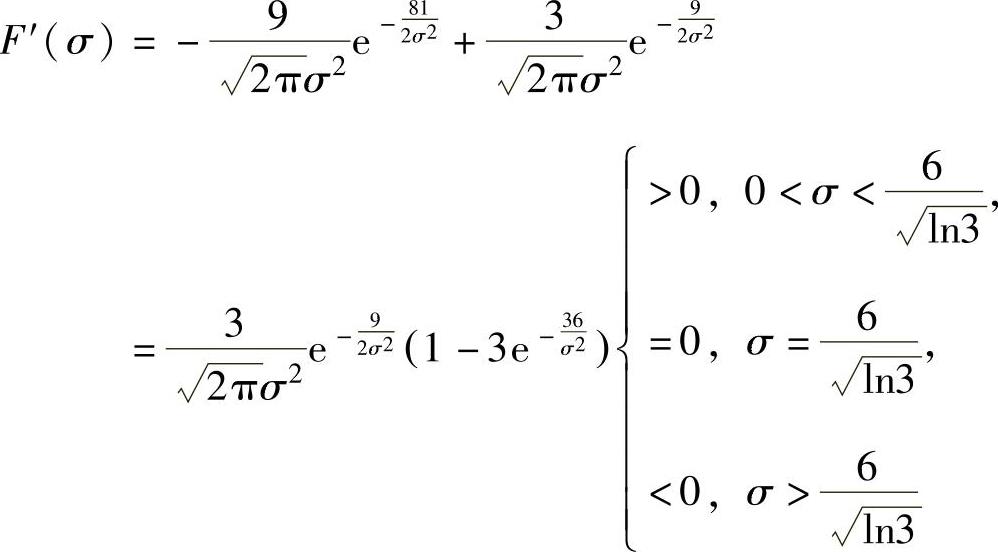
知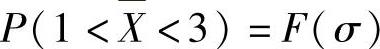 在
在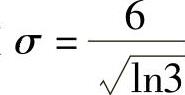 处取最大值.
处取最大值.
