练习题六解答
1.单项选择题
(1)D (2)C (3)A (4)D (5)D (6)B
(7)D (8)B (9)A (10)B (11)C (12)B
(13)D (14)D (15)D (16)D (17)B (18)C
(19)A (20)D (21)B (22)B (23)C (24)C
(25)C (26)C (27)A
2.解答题
(1)所给方程组的系数矩阵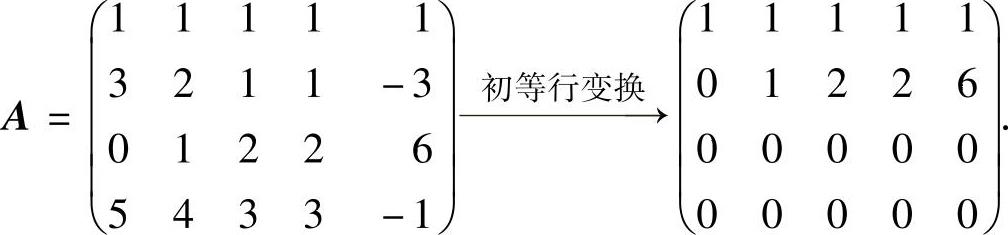 所
所
以,r(A)=2,容易检验,α1,α2,α3,α4都是所给方程组的解向量,因此由α1,α2,α3线性无关知其为一个基础解系;由α1,α2,α4线性相关知其不为一个基础解系.
(2)系数行列式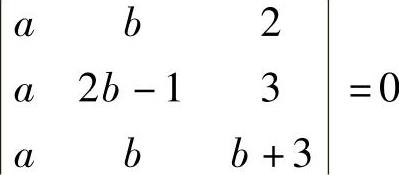 得a=0或b=-1,1,仅在此时,方程组有可能有无穷多解.
得a=0或b=-1,1,仅在此时,方程组有可能有无穷多解.
当a=0时,增广矩阵
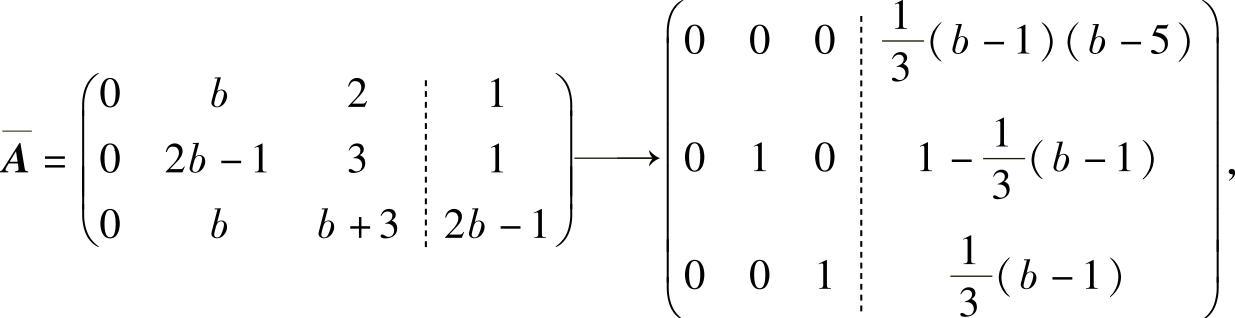
由此可知此时仅当b=5时,所给方程组有无穷多解,通解为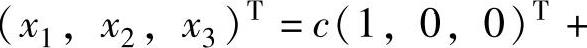
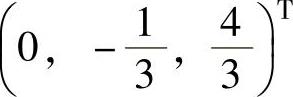 ,其中,c为任意常数.
,其中,c为任意常数.
当b=1时,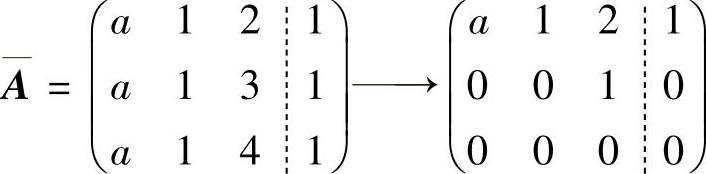 ,所给方程组有无穷多解,通解为
,所给方程组有无穷多解,通解为
(x1,x2,x3)T=c1(1,-a,0)T+(0,1,0)T.
当b=-1时,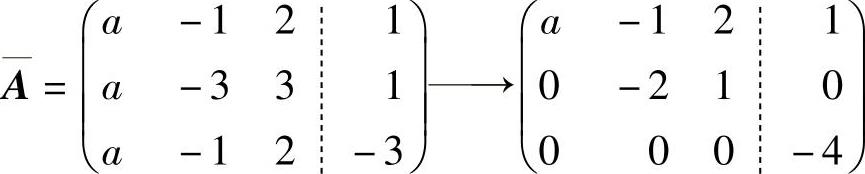 ,此时方程组无解.
,此时方程组无解.
(3)η1-η3=(η1+η2)-(η2+η3)=(1,3,2)T,η2-η3=(η1+η2)-(η1+η3)=(0,2,4)T都是Ax=0的解,且线性无关.于是由r(A)=1知η1-η3,η2-η3是Ax=0的一个基础解系,此外,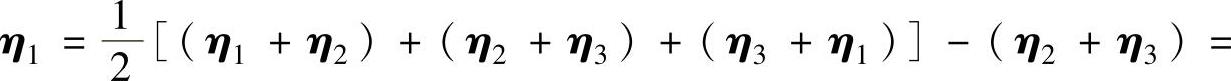
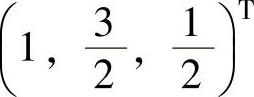 是Ax=b的一个特解,从而Ax=b的通解为
是Ax=b的一个特解,从而Ax=b的通解为
(x1,x2,x3)T=c1(η1-η3)+c2(η2-η3)+η1=c1(1,3,2)+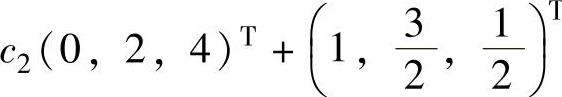 ,其中,c1,c2,c3为任意常数.
,其中,c1,c2,c3为任意常数.
(4)(ⅰ)设有数k1,k2使得
k1η1+k2(η1-η2)=0,即(k1+k2)η1-k2η2=0上式两边左乘A得k1b=0.由b≠0得k1=0.于是由k2(η1-η2)=0得k2=0(因为η1-η2≠0).从而η1与η1-η2线性无关.
(ⅱ)由于ξ,η1-η2都是Ax=0的解,所以由r(A)=n-1知ξ,η1-η2线性相关,即存在不全为零的数λ1,λ2,使得
λ1ξ+λ2(η1-η2)=0,即λ1ξ+λ2η1+(-λ2)η2=0.
由此知,ξ,η1,η2线性相关.
(5)由α1,α2是A∗x=0的两个解,且α1,α2线性无关,所以r(A∗)≤3-2=1.由A知r(A∗)≥1,因此r(A∗)=1,由此得到r(A)=2.于是由
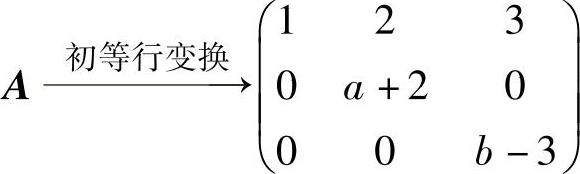
知a=-2,b≠3,或a≠-2,b=3.
(6)由r(A)=4-2=2及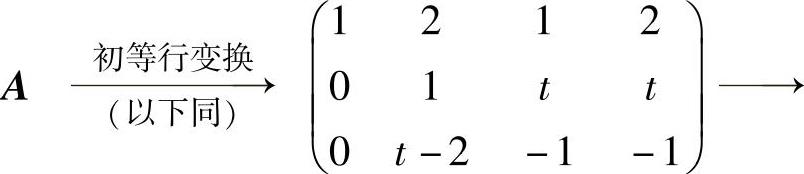
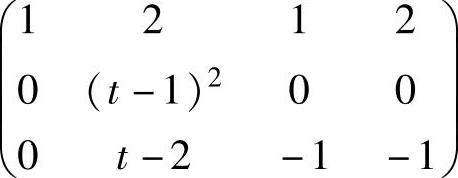 知t=1.所以
知t=1.所以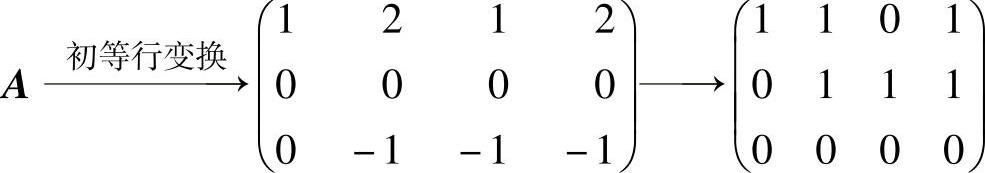 ,
,
从而Ax=0与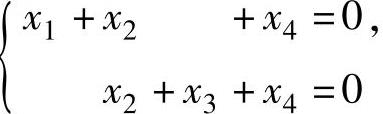 同解,其基础解系为(1,-1,1,0)T和(0,-1,0,
同解,其基础解系为(1,-1,1,0)T和(0,-1,0,
1)T.所以通解为(x1,x2,x3,x4)T=c1(1,-1,1,0)T+c2(0,-1,0,1)T.
(7)(ⅰ)由于所给方程组有3个线性无关的解,所以其导出组Ax=0(x=(x1,x2,x3,x4)T)的基础解系至少由两个解向量组成,从而r(A)≤4-2=2.另外,由A知r(A)≥2,所以r(A)=2.
(ⅱ)由增广矩阵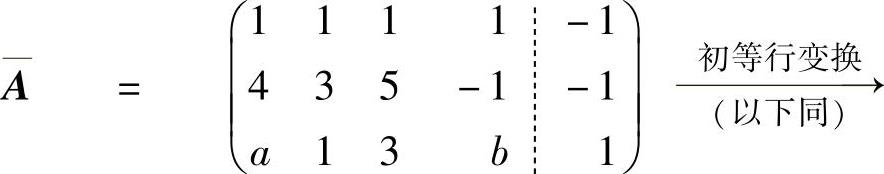
 及r(A)=2知a=
及r(A)=2知a=
2,b=-3.
于是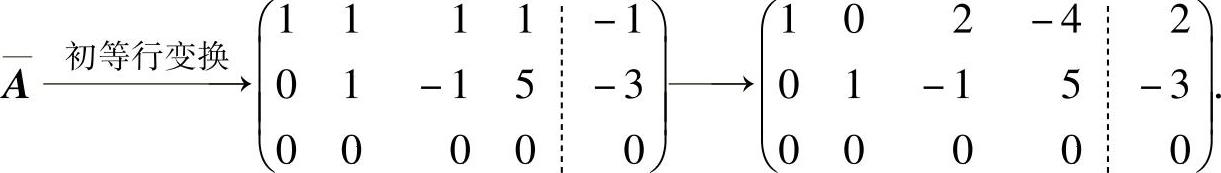
由此可得,导出组的基础解系为(-2,1,1,0)T,(4,-5,0,1)T,所给方程组有特解(2,-3,0,0)T,所以通解为
(x1,x2,x3,x4)T=c1(-2,1,1,0)T+c2(4,-5,0,1)T+(2,-3,0,0)T
(8)(Ⅱ)的通解为(x1,x2,x3,x4)T=c(-3,2,1,0)T+(-2,5,0,-10)T,即
x1=-3c-2,x2=2c+5,x3=c,x4=-10.
将它们代入(Ⅰ)得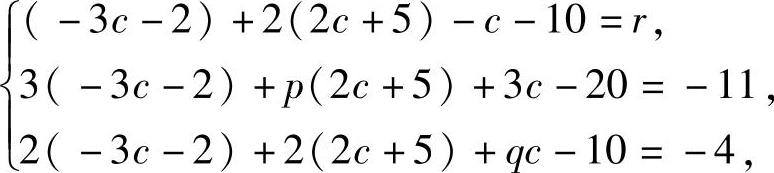 即
即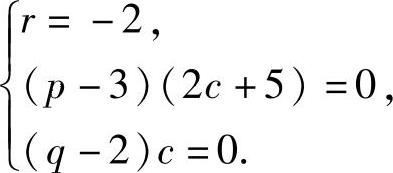
由于c是任意常数,所以,p=3,q=2,r=-2.
(9)设有数k1,k2,…,kr,k使得
k1α1+k2α2+…+krαr+kβ=0,(1)上式两边左乘βT得k1βTα1+k2βTα2+…+krβTαr+kβTβ=0.
由题设知αTiβ=0,即βTαi=0(i=1,2,…,r).因此由上式得kβTβ=0.于是由β≠0得k=0,将它代入式(1)得k1α1+k2α2+…+krαr=0.于是由α1,α2,…,αr线性无关得k1=k2=…=kr=0,因此α1,α2,…,αr,β线性无关.
(10)记系数矩阵为A,则A=0,即

由此得到a=0,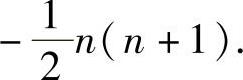
当a=0时,r(A)=1,此时所给方程组通解为
(x1,x2,…,xn)T=c1(-1,1,0,…,0)T+c2(-1,0,1,…,0)T+…+
cn-1(-1,0,0,…,1)T.
当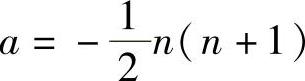 时,r(A)=n-1,此时所给方程组通解为(x1,x2,…,xn)T=c(1,2,…,n)T.
时,r(A)=n-1,此时所给方程组通解为(x1,x2,…,xn)T=c(1,2,…,n)T.
(11)由于方程组(Ⅰ)的增广矩阵

所以方程组(Ⅰ)与方程组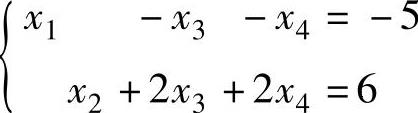
,
同解,即与(Ⅱ)同解.
(12)方程组(Ⅰ)的通解为
(x1,x2,x3,x4)T=c1(1,0,1,1)T+c2(2,1,0,-1)T+c3(0,2,1,-1)T
=(c1+2c2,c2+2c3,c1+c3,c1-c2-c3)T.(https://www.daowen.com)
将它代入方程组(Ⅱ)得
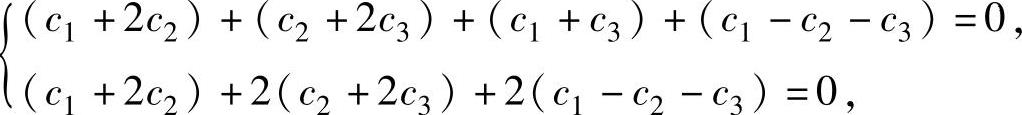
即 3c1+2c2+2c3=0,即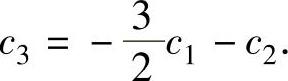
因此公共解为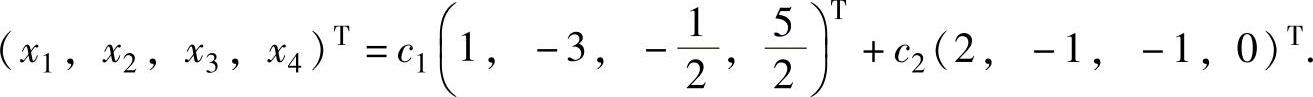
(13)由0·E3-A=-A=0,(-1)E3-A=-A+E3=0知A有特征值λ1=0,λ2=-1.此外还有特征值λ3,它满足λ1+λ2+λ3=trA=0,所以λ3=1.
(14)设A的特征值为λ,则λ满足λ3+λ2+λ=3,它只有实根λ=1,即A只有特征值λ=1,因此存在正交矩阵Q,使得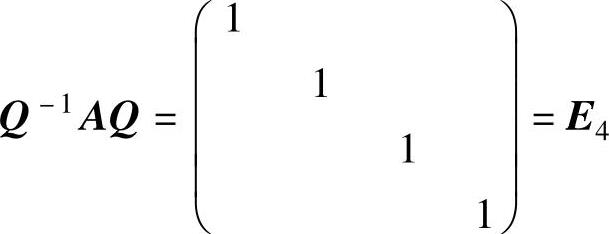 ,故A=QE4Q-1=E4.
,故A=QE4Q-1=E4.
(15)由AAT=2E4得A2=16,所以A=-4,对λ有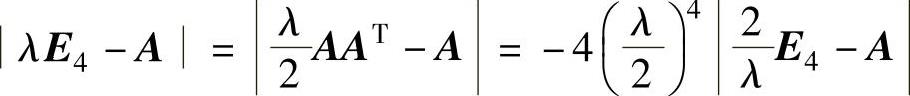 ,
,
于是,当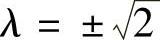 时,上式成为
时,上式成为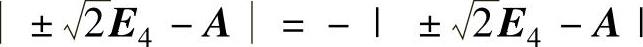 .由此得到
.由此得到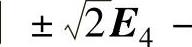
A=0,所以,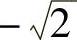 ,
, 是A的两个特征值,从而
是A的两个特征值,从而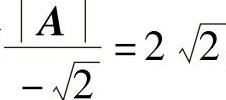 ,
,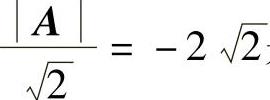 是A∗的两个
是A∗的两个
特征值.
(16)由λE3-A=(λ-1)2(λ-3)知A的特征值为λ=3,1(二重).由于(1·E3-
A)的秩为1=3(A的阶数)-2(λ=1的重数),所以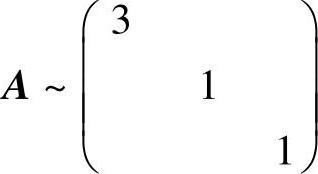 ,从而A100能相似对角
,从而A100能相似对角
化为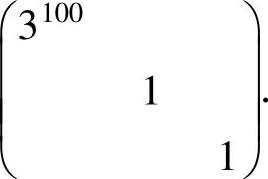
(17)设A-1的特征向量α对应的特征值为λ0,则α是A的对应特征值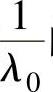 的特征向量,
的特征向量,
于是有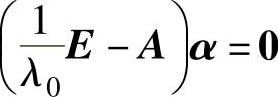 ,即
,即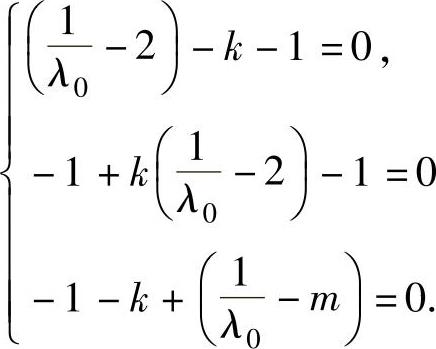 ,由此得k=-2,m=2或k=1,m=2.
,由此得k=-2,m=2或k=1,m=2.
(18)由题设知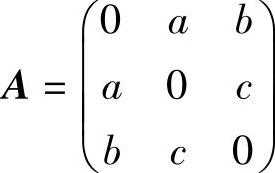 ,且(2E3-A)α=0,即
,且(2E3-A)α=0,即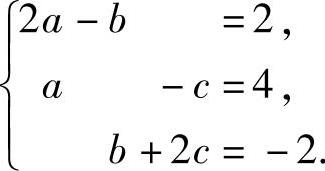 解此方程
解此方程
组得a=2,b=2,c=-2,所以
(19)由α1,α2是Ax=0的两个解知,A有特征值λ=0,α1,α2是它对应的两个线性无关的特征向量.此外,由A的各行元素之和都为3知A有特征值3,它对应的特征向量为β=(1,1,1)T.于是A的全部特征值为0,3,对应的特征向量为c1α1+c2α2(c1,c2是任意不全为零的常数),cβ(c是非零任意常数).
(20)由题设得A∗x=λ0x,即λ0Ax=Ax,将x=(-1,-1,1)T和A=-1代
入上式得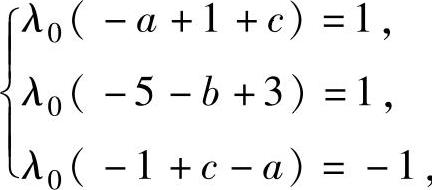 即λ0=1,a=c,b=-3.于是由-1=A=a-3得
即λ0=1,a=c,b=-3.于是由-1=A=a-3得
a=c=2.
(21)分两种情形证明AB的特征值必是BA的特征值:
(ⅰ)设λ是AB的非零特征值,其对应的特征向量为α,则
A(Bα)=λα,即(BA)(Bα)=λ(Bα).由于Bα≠0,所以λ是BA的特征值.
(ⅱ)设λ=0是AB的特征值,其对应的特征向量α,即(AB)α=0,则齐次线性方程组(AB)x=0有非零解.于是BA=AB=0,由此得到齐次线性方程组(BA)x=0有非零解,于是λ=0也是BA的特征值.
同理可证BA的特征值也是AB的特征值,因此AB有相同特征值.
(22)设r(A)=r,r(B)=s,则r<n,s<n,所以齐次线性方程组Ax=0与Bx=0分别有基础解系α1,α2,…,αn-r和β1,β2,…,βn-s.由于r+s<n,所以α1,α2,…,αn-r,β1,β2,…,βn-1线性相关,因此存在不全为零的数k1,k2,…,kn-r和λ1,λ2,…,λn-s,使得
k1α1+k2α2+…+kn-rαn-r+λ1β1+λ2β2+…+λn-sβn-s=0.(1)
记γ=k1α1+k2α2+…+kn-rαn-r=-(λ1β1+λ2β2+…+λn-sβn-s),则由α1,α2,…,αn-r线性无关与β1,β2,…,βn-s线性无关知γ≠0,并且有Aγ=0与Bγ=0.因此γ是A与B的对应特征值为0的公共特征向量.
(23)f的矩阵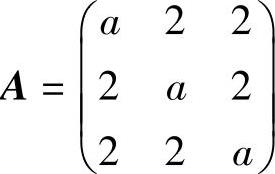 ,它有特征值λ=6,0,0.所以由trA=6得a=2.
,它有特征值λ=6,0,0.所以由trA=6得a=2.
(24)(ⅰ)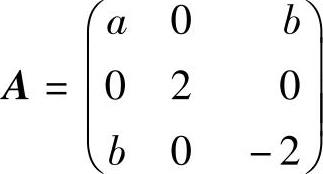 ,设它的特征值为λ1,λ2,λ3,则
,设它的特征值为λ1,λ2,λ3,则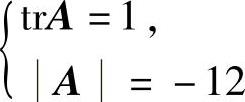 {,由此得
{,由此得
a=1,b=2.
(ⅱ)由(ⅰ)知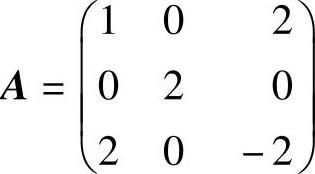 ,它有特征值λ=-3,2(二重),且对应λ=-3的特
,它有特征值λ=-3,2(二重),且对应λ=-3的特
征向量为α1=(1,0,-2)T,对应λ=2的特征向量为α2=(0,1,0)T,α3=(2,0,1)T,
将它们正交单位化后得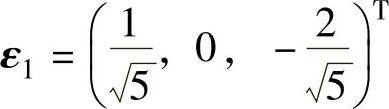 ,ε2=(0,1,0)T,
,ε2=(0,1,0)T,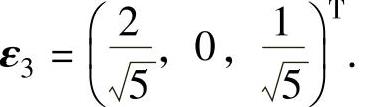
记Q=(ε1,ε2,ε3),则在正交变换(x1,x2,x3)T=Q(y1,y2,y3)T下,f(x1,x2,x3)=-3y21+2y22+2y23(标准形).
(25)f的矩阵
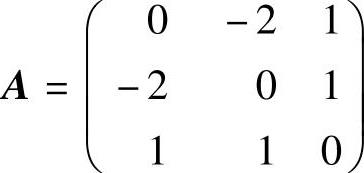
的秩为3,由于λE3-A=0的根为λ=2,-1- ,
,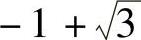 ,所以f的正惯性指数为2.
,所以f的正惯性指数为2.
(26)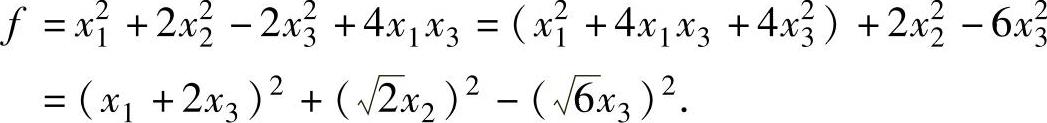
记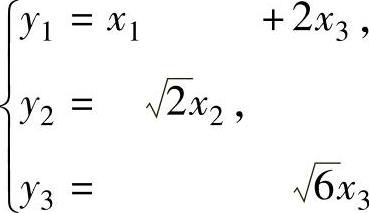 即
即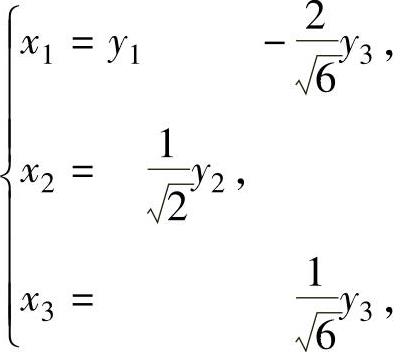 所以
所以 则在x
则在x
=Py(x=(x1,x2,x3)T,y=(y1,y2,y3)T)下,f=y21+y22-y23(规范形).
(27)记x=(x1,x2,…,xn)T,y=(y1,y2,…,ys)T,则y=Ax,且f=y21+y22+…+y2s=(y1,y2,…,ys)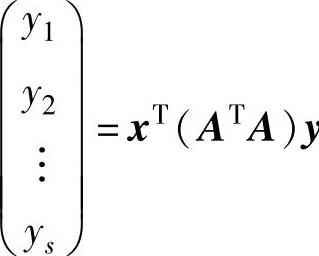 ,所以f的矩阵为B=ATA.由于r(B)=r(A)(这是由于方程组ATAx=0与Ax=0同解),所以f的秩为r(A).
,所以f的矩阵为B=ATA.由于r(B)=r(A)(这是由于方程组ATAx=0与Ax=0同解),所以f的秩为r(A).
(28)(ⅰ)f的矩阵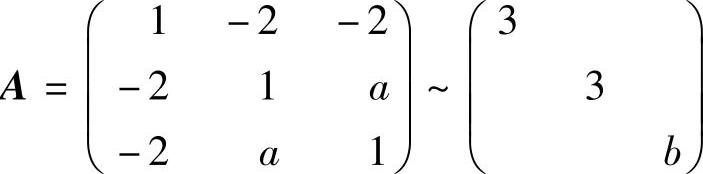 ,所以由trA=3+3+b,即
,所以由trA=3+3+b,即
b=-3.由于3是A的特征值,所以由3E3-A=0得a=-2.
(ⅱ)由(ⅰ)知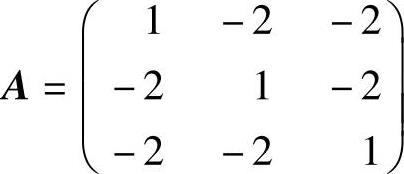 ,且它的特征值为λ=-3,3(二重).
,且它的特征值为λ=-3,3(二重).
对应特征值λ=-3的特征向量α1=(1,1,1)T,对应特征值λ=3的特征向量α2=(-1,1,0)T,α3=(-1,0,1)T.
将α1,α2,α3正交单位化后得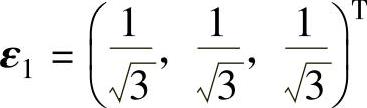 ,
,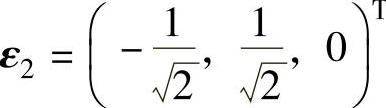 ,
,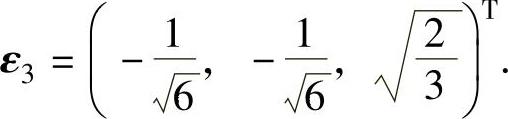 所以正交矩阵
所以正交矩阵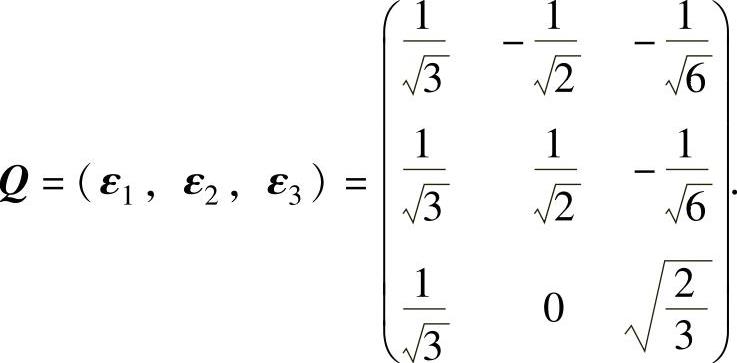
(ⅲ)在正交变换x=Qy下,2=xTx=yTy,即y21+y22+y23=2.于是
f(x1,x2,x3)=3y21+3y22-3y23≤3(y21+y22+y23)=6(最大值).
(29)f的矩阵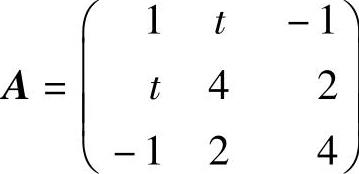 ,欲使f为正定二次型,必须满足
,欲使f为正定二次型,必须满足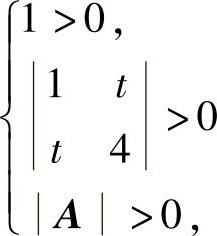 ,即-2<t<1,
,即-2<t<1,
所以当t∈(-2,1)时,f为正定二次型.
(30)f的矩阵为
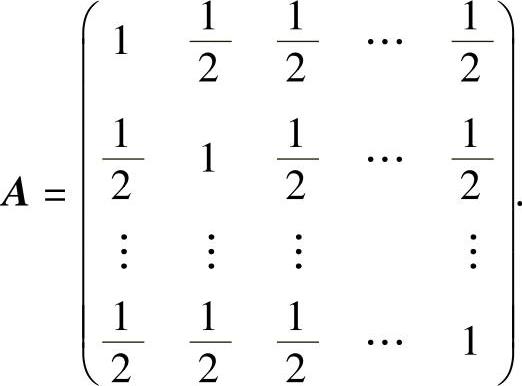
由于顺序主子式1>0,以,f是正定二次型.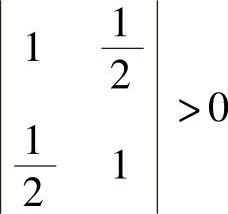 ,…,
,…,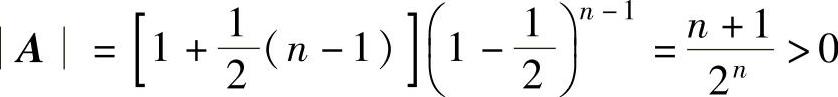 ,所
,所
