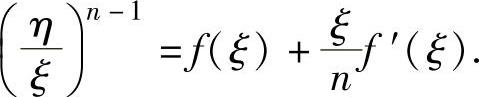练习题一
1.单项选择题
(1)设数列{xn},{yn},{zn}满足yn≤xn≤zn(n=1,2,…),并且nl→im∞(zn-yn)=0,
则limxn().
n→∞
A.存在且等于零 B.存在但不一定为零
C.一定不存在 D.不一定存在
(2)x→0时的三个无穷小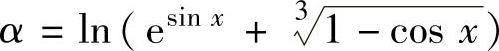 ,β
,β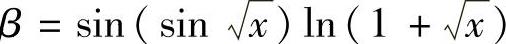 及
及
γ=1-cos(arcsinx)按阶数由低到高排列为().
A.α,β,γ B.β,α,γ C.γ,α,β D.β,γ,α
(3)设函数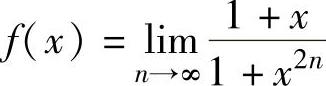 ,则f(x)( ).
,则f(x)( ).
A.不存在间断点 B.存在间断点x=1
C.存在间断点x=0 D.存在间断点x=-1
(4)已知极限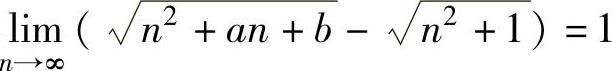 ,则a,b的值分别为( ).
,则a,b的值分别为( ).
A.a=1,b=2 B.a=2,b=1
C.a=1,b任意 D.a=2,b任意
(5)设函数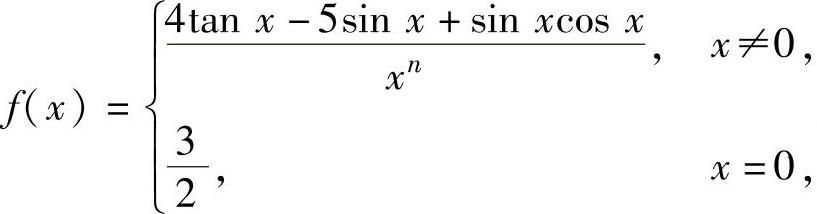 则f(x)在
则f(x)在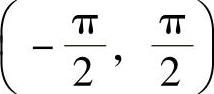 内连续时,n为( ).
内连续时,n为( ).
A.1 B.2 C.3 D.4
(6)设函数f(x)在点x=0处连续,则下列命题错误的是().
A.若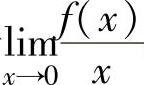 存在,则f(0)=0B.若
存在,则f(0)=0B.若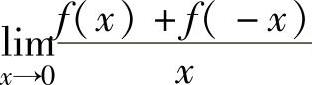 存在,则f(0)=0
存在,则f(0)=0
C.若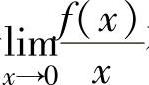 存在,则f′(0)=0D.若lim
存在,则f′(0)=0D.若lim
x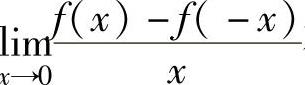 存在,则f′(0)=0
存在,则f′(0)=0
(7)设函数f(x)可导,F(x)=f(x)(1+|sinx|).如果F(x)在点x=0处可导,则必有( ).
A.f(0)=0 B.f′(0)=0
C.f(0)+f′(0)=0 D.f(0)-f′(0)=0
(8)函数y=(x2-x)|x3-x|的不可导点个数为( ).
A.0 B.1 C.2 D.3
(9)设f(x)是不恒为零的奇函数,f′(0)存在,则函数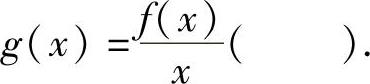
A.在点x=0处左极限不存在 B.有跳跃间断点
C.在点x=0处右极限不存在 D.有可去间断点
(10)设函数f(x)=|x3-1|φ(x),其中φ(x)在点x=1处连续,则φ(1)=0是f(x)在点x=1处可导的( ).
A.充分而非必要条件 B.必要而非充分条件
C.充分必要条件 D.既非充分也非必要条件
(11)设(x0,y0)是抛物线y=ax2+bx+c上的一点,若在该点处的切线通过原点,则a,b,c及x0应满足的关系为( ).
A.a=cx20,b任意 B.c=ax20,b任意
C.b=cx20,a任意 D.c=bx20,a任意
(12)设函数y=f(x)具有二阶导数,且f′(x)>0,f″(x)>0,Δx为自变量x在点x0处的增量,Δy与dy分别为f(x)在点x0处的增量与微分,若Δx>0,则( ).
A.0<dy<Δy B.0<Δy<dy C.Δy<dy<0 D.dy<Δy<0
(13)设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( ).
A.当x∈(0,δ)时,f(x)单调增加 B.当x∈(-δ,0)时,f(x)单调减少
C.当x∈(0,δ)时,f(x)>f(0) D.当x∈(-δ,0)时,f(x)>f(0)
(14)设函数f(x)的导数f′(x)在点x=a处连续,且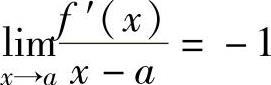 ,则( ).
,则( ).
A.x=a是f(x)的极小值点
B.x=a是f(x)的极大值点
C.(a,f(a))是曲线y=f(x)的拐点
D.x=a不是f(x)的极值点,(a,f(a))也不是曲线y=f(x)的拐点
(15)设函数f(x)在(-∞,+∞)上连续,其导函数的图形如图题1.1(15)所示,则f(x)有( ).
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点
(16)设在[0,1]上,函数f(x)二阶可导,且f″(x)>0,则f′(0),f′(1),f(1)-f(0)或f(0)-f(1)的大小顺序是( ).
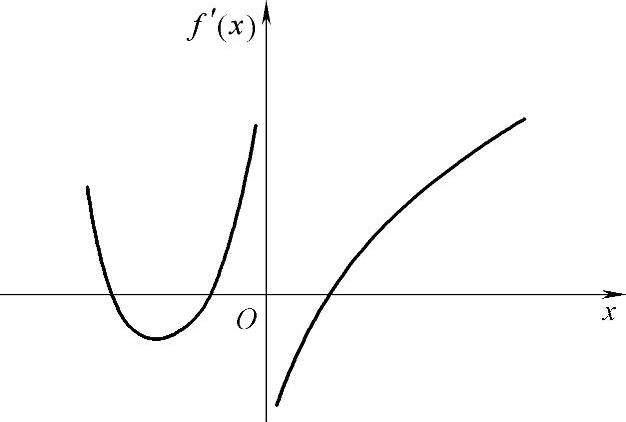
图 题1.1(15)
A.f′(1)>f′(0)>f(1)-f(0)
B.f′(1)>f(1)-f(0)>f′(0)
C.f(1)-f(0)>f′(0)>f′(1)
D.f′(1)>f(0)-f(1)>f′(0)
(17)设函数f(x)满足关系式f″(x)-2f′(x)+4f(x)=0,且f(x0)>0,f′(x0)=0,则f(x)( ).(https://www.daowen.com)
A.在点x0处有极大值 B.在点x0处有极小值
C.在点x0的某个邻域内单调增加 D.在点x0的某个邻域内单调减少
(18)设方程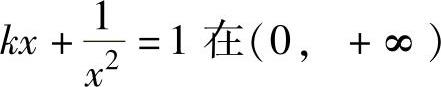 有且仅有一个实根,则k的取值范围为( ).
有且仅有一个实根,则k的取值范围为( ).
A.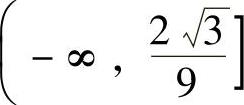 B.
B.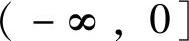
C.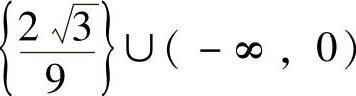 D.
D.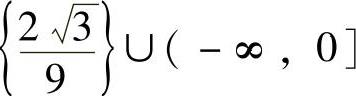
(19)设曲线y=x3+3ax2+3bx+c在点x=-1处取得极值,且点(0,3)是拐点,则a,b,c为( ).
A.a=-1,b=0,c=3 B.a=0,b=-1,c=3
C.a=3,b=-1,c=0 D.a=0,b=3,c=-1
(20)设(x0,f(x0))是曲线y=f(x)的拐点,则( ).
A.x0不是函数f(x)的极值点
B.f″(x)在点x0的两侧邻近有不同的符号
C.f″(x0)=0
D.曲线y=f(x)经过点(x0,f(x0))时,凹凸性发生变化
(21)设函数f(x)在(-∞,+∞)上连续,x0≠0,f(x0)≠0,且(x0,f(x0))是曲线y=f(x)的拐点,则( ).
A.f″(x0)=0
B.(x0,-f(x0))是曲线y=-f(x)的拐点
C.(-x0,f(-x0))不是曲线y=f(-x)的拐点
D.(-x0,-f(x0))不是曲线y=-f(-x)的拐点
(22)曲线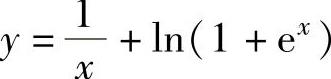 的渐近线的条数为( ).
的渐近线的条数为( ).
A.0 B.1 C.2 D.3
(23)曲线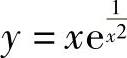 ( ).
( ).
A.仅有水平渐近线 B.仅有铅直渐近线
C.既有水平渐近线又有铅直渐近线 D.既有铅直渐近线又有斜渐近线
2.解答题
(1)计算极限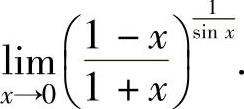
(2)计算极限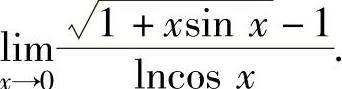
(3)计算极限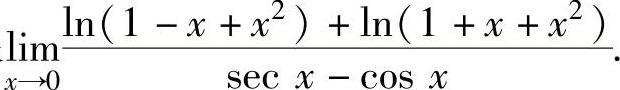
(4)计算极限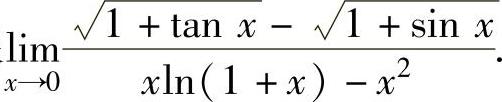
(5)计算极限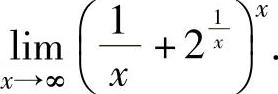
(6)计算极限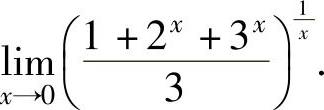
(7)计算极限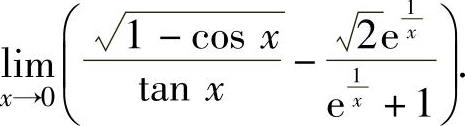
(8)计算极限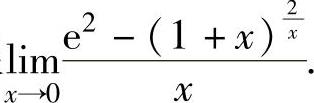
(9)确定当x→0时,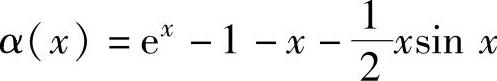 是x的几阶无穷小.
是x的几阶无穷小.
(10)设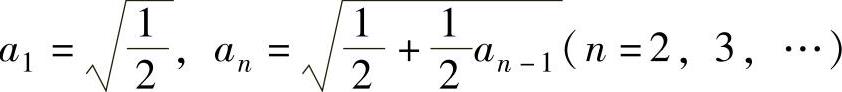 ,求极限lim
,求极限lim
n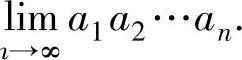
(11)设函数f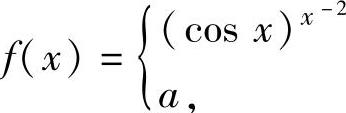
,x≠0,
{x=0在点x=0处连续,求常数a的值.
(12)求能够使函数f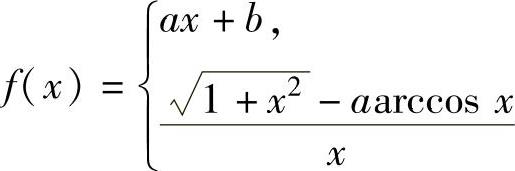
x≤0,
连续的常数a,b的值.,x>0
(13)求函数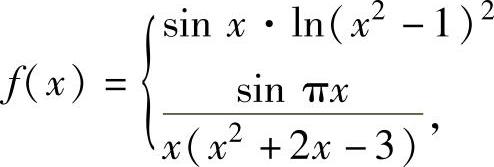
,x≤0,
{x>0的间断点,并指明它们的类型.
(14)设函数y=xsinx+2tan2x,求y′.
(15)设函数y=xexsinx,求y(4).
(16)已知函数f(x)在(-∞,+∞)上可导,且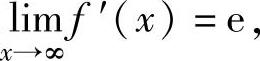
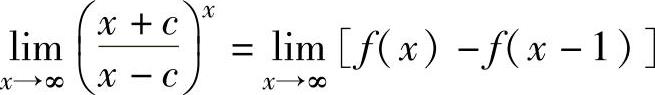 ,
,
求常数c.
(17)设函数f(x)=xex,求f(n)(x)的极小值.
(18)设函数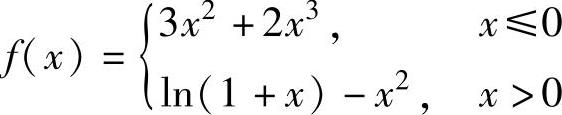
,
{,求f′(x)的极小值.
(19)设x∈(0,1),证明: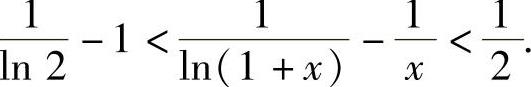
(20)设常数k>0,求方程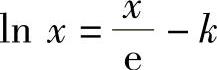 在(0,+∞)上的实根个数.
在(0,+∞)上的实根个数.
(21)设函数f(x)在[0,1]上连续,在(0,1)内可导,且f(1)=0.证明:存在ξ∈(0,1),使得
ξf′(ξ)+2f(ξ)=0.
(22)设函数f(x)在[a,b](a>0)上连续,在(a,b)内可导,且f(a)=f(b)=1.证明:存在ξ,η∈(a,b),使得