练习题六
1.单项选择题
(1)设非齐次线性方程组Ax=b(其中,A是m×n矩阵),则下列结论中正确的是( ).
A.若Ax=0仅有零解,则Ax=b有唯一解
B.若Ax=0有非零解,则Ax=b有无穷多解
C.若Ax=b有无穷多解,则Ax=0仅有零解
D.若Ax=b有无穷多解,则Ax=0有非零解
(2)记齐次线性方程组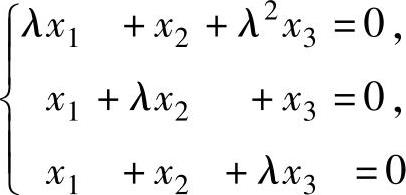 的系数矩阵为A,若存在三阶矩阵B≠O3,使得AB=O3,则().
的系数矩阵为A,若存在三阶矩阵B≠O3,使得AB=O3,则().
A.λ=-2且B=0 B.λ=-2但B≠0
C.λ=1且B=0 D.λ=1但B≠0
(3)线性方程组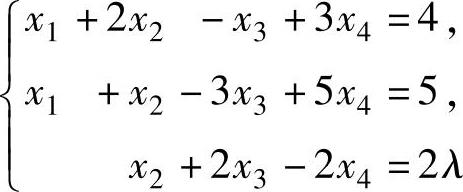 有解时,λ的值为( ).
有解时,λ的值为( ).
A.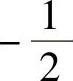 B.
B.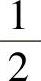 C.-1 D.1
C.-1 D.1
(4)非齐次线性方程组Ax=b(其中,A是m×n矩阵)有解的必要条件是().
A.m>n B.m<n
C.m=n D.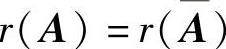 (其中,A=(A︙b))
(其中,A=(A︙b))
(5)设n阶矩阵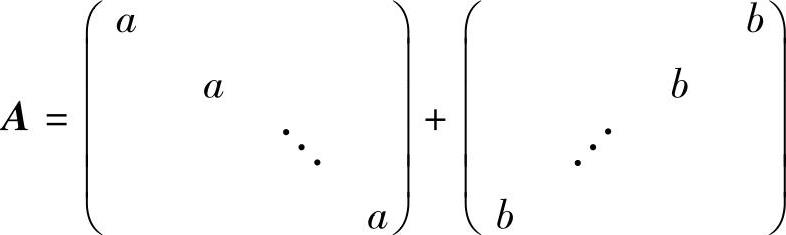 (其中,a≠0,b≠0),则齐次线性方程组Ax=0有非零解的充分必要条件是( ).
(其中,a≠0,b≠0),则齐次线性方程组Ax=0有非零解的充分必要条件是( ).
A.a=b
B.a+b=0
C.n=2m时,a=b;n=2m+1时,a+b=0
D.n=2m时,a=b;n=2m+1时,a=b或a+b=0
(6)已知α1,α2,α3是齐次线性方程组Ax=0的基础解系,则该方程组的基础解系还可以是( ).
A.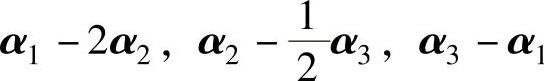 B.α1+α2,α2+α3,α3+α1
B.α1+α2,α2+α3,α3+α1
C.α1-α2,α2-α3,α3-α1D.-2α3-α1,α1+α2+α3,α3-α2
(7)设A是n阶矩阵,α是n维列向量,若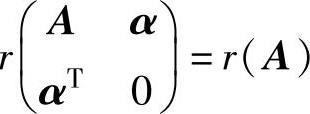 ,则线性方程组( ).
,则线性方程组( ).
A.Ax=α必有无穷多解B.Ax=α必有唯一解
C.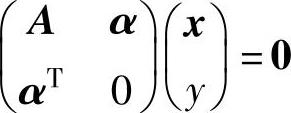 仅有零解D.
仅有零解D.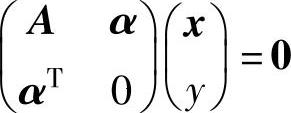 必有非零解
必有非零解
(8)设n阶矩阵A的伴随矩阵A∗≠0.若ξ1,ξ2,ξ3是非齐次线性方程组Ax=b的三个互不相等的解向量,则对应的齐次线性方程组Ax=0的基础解系( ).
A.不存在 B.仅含有一个非零解向量
C.含有两个线性无关的解向量 D.含有三个线性无关的解向量
(9)设A为n阶实矩阵,AT是A的转置矩阵,齐次线性方程组(Ⅰ)Ax=0和(Ⅱ)ATAx=0,则( ).
A.(Ⅱ)的解是(Ⅰ)的解,(Ⅰ)的解也是(Ⅱ)的解
B.(Ⅱ)的解是(Ⅰ)的解,但(Ⅰ)的解不是(Ⅱ)的解
C.(Ⅰ)的解是(Ⅱ)的解,但(Ⅱ)的解不是(Ⅰ)的解
D.(Ⅰ)的解不是(Ⅱ)的解,(Ⅱ)的解也不是(Ⅰ)的解
(10)设有齐次线性方程组Ax=0和Bx=0,其中A,B都是m×n矩阵,现有以下4个命题:
① 若Ax=0的解都是Bx=0的解,则r(A)≥r(B)
② 若r(A)≥r(B),则Ax=0的解都是Bx=0的解
③ 若Ax=0与Bx=0同解,则r(A)=r(B)
④ 若r(A)=r(B),则Ax=0与Bx=0同解则正确的是().
A.①② B.①③ C.②④ D.③④
(11)设三阶矩阵A的特征值为-1,1,2,则矩阵(3A∗)-1的特征值为( ).A.1,-1,-2 B.-6,6,-3 C.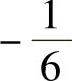 ,
,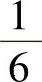 ,
,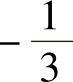 D.
D.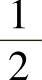 ,
,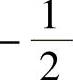 ,-1
,-1
(12)设A,B都是n阶矩阵,则以下命题中正确的是( ).
A.A的特征向量的任意线性组合仍是A的特征向量
B.设λ是可逆矩阵A的特征值,则A的对应λ的特征向量也是A-1的对应λ1的特征向量
C.A与AT有相同的特征向量
D.如果A~B,则A与B有相同的特征向量
(13)设A是三阶矩阵,αi(i=1,2,3)都是3维列向量,如果Aαi=iαi(i=1,2,3),则下列结论中成立的是( ).
A.如果P=(α1,2α2,3α3),则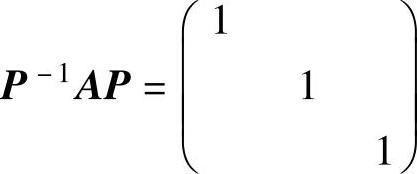
B.如果P=(α1,α1+α2,3α3),则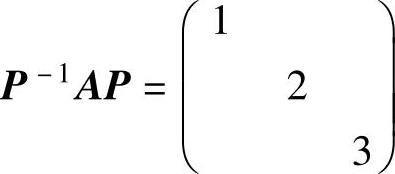
C.如果P=(2α1,-α2,5α3),则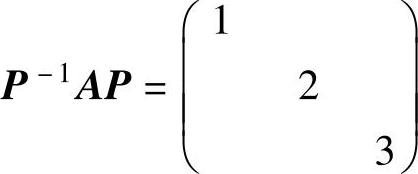
D.如果P=(α1,α2,α3),则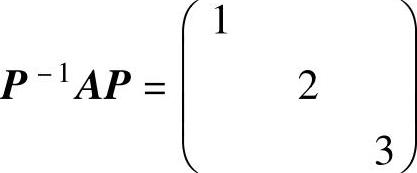
(14)设n阶矩阵A=(aij)的特征值为λ1,λ2,…,λn,则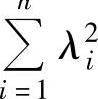 的值为( ).
的值为( ).
A.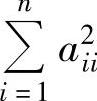 B.
B.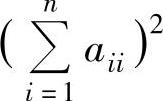 C.
C.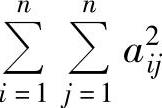 D.
D.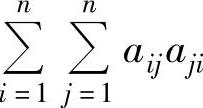
(15)n阶矩阵A与B相似的充分条件是( ).
A.A=B
B.r(A)=r(B)
C.A与B有相同的特征多项式
D.A与B的特征值都为λ1,λ2,…,λn,且这n个特征值是互异的
(16)设A是n阶非零矩阵,满足Ak=On(其中k为正整数),则下列命题中不正确的是( ).
A.A只有零特征值 B.A必不能相似对角化C.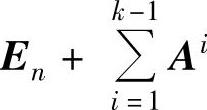 必可逆D.A只有一个线性无关的特征向量
必可逆D.A只有一个线性无关的特征向量
(17)下列矩阵中,不能相似于对角矩阵的是( ).
A.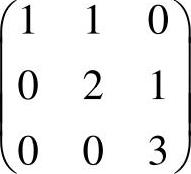 B.
B.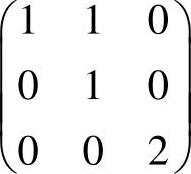 C.
C. D.
D.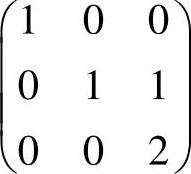
(18)设矩阵A相似于矩阵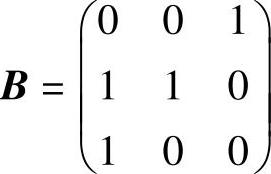 ,则r(A-2E4)+r(A-E4)=( ).
,则r(A-2E4)+r(A-E4)=( ).
A.2 B.3 C.4 D.5
(19)设二次型f(x1,x2,x3)=(x1+x2)2+(x2+x3)2+(x3+x1)2,则f的( ).
A.秩为3 B.矩阵为E3
C.正惯性指数为2 D.以上都不对
(20)设A,B都是n阶实对称矩阵,则A与B合同的充分必要条件是( ).
A.r(A)=r(B)
B.A,B的全部特征值相同
C.A=B
D.分别以A,B为矩阵的二次型有相同的规范形
(21)设A是n阶矩阵,则以下四个命题中正确的是( ).
A.A必与某个对角矩阵合同(https://www.daowen.com)
B.如果A与正定矩阵合同,则A为正定矩阵
C.如果A的顺序主子式都大于零,则A必为正定矩阵
D.如果A与对角矩阵相似,则A必与对角矩阵合同
(22)设n阶矩阵A=(aij)是正定矩阵,b1,b2,…,bn是全不为零的实数,则n阶矩阵B=(bibjaij)是( ).
A.对称而非正定矩阵 B.正定矩阵
C.可逆而非正定矩阵 D.不可逆矩阵
(23)当两个3元二次型f(x1,x2,x3)=xTAx与g(x1,x2,x3)=xTBx(其中,x=(x1,x2,x3)T)的实对称矩阵A与B合同时,称它们是属于同一类的,则全体三元二次型可以分成( ).
A.3类 B.6类 C.10类 D.无穷多类
(24)设A是n阶正定矩阵,如果它与n阶矩阵B相似,则B必为( ).
A.实对称矩阵 B.正交矩阵 C.可逆矩阵 D.正定矩阵
(25)已知二次型f(x1,x2,x3)的矩阵为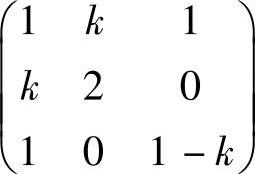 ,如果f的正惯性指数为3,则k=( ).
,如果f的正惯性指数为3,则k=( ).
A.0B.-1C.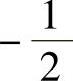 D.1
D.1
(26)n阶实对称矩阵A为正定矩阵的充分必要条件是( ).
A.A的所有k阶子式都大于零(k=1,2,…,n)
B.A的所有特征值都为非负的
C.A-1为正定矩阵
D.r(A)=n
(27)设A,B都是n阶正定矩阵,则下列选项中是正定矩阵的是( ).
A.A∗+B∗ B.A∗-B∗
C.A∗B∗ D.k1A∗+k2B∗(k1,k2是常数)
2.解答题
(1)设有齐次线性方程组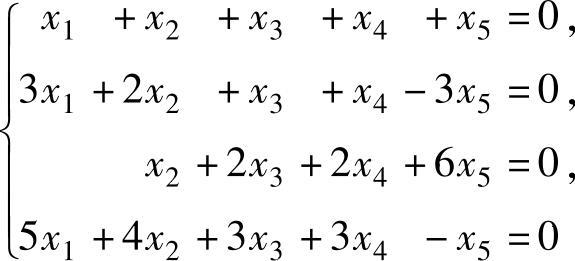 及向量α1=(1,-2,1,0,
及向量α1=(1,-2,1,0,
0)T,α2=(1,-2,0,1,0)T,α3=(5,-6,0,0,1)T,α4=(1,-2,-1,2,0)T,问向量组α1,α2,α3与向量组α1,α2,α4是否为所给方程组的基础解系?
(2)问a,b为何值时,线性方程组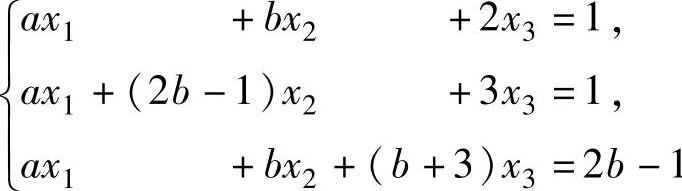 有无穷多解,
有无穷多解,
并求其通解.
(3)设三元非齐次线性方程组Ax=b的系数矩阵A的秩为1,且η1,η2,η3是它的三个解向量,它们满足
η1+η2=(1,2,3)T,η2+η3=(0,-1,1)T,η3+η1=(1,0,-1)T.求该方程组的通解.
(4)设η1,η2是非齐次线性方程组Ax=b的两个不同解(其中,A是m×n矩阵),ξ是该方程组的导出组的一个非零解.
(ⅰ)判定向量组η1,η1-η2的线性相关性;
(ⅱ)当r(A)=n-1时,判定ξ,η1,η2的线性相关性.
(5)设α1=(1,0,1)T,α2=(0,1,1)T是齐次线性方程组A∗x=0的两个解,其中 ,求a,b的值.
,求a,b的值.
(6)设矩阵 ,且齐次线性方程组Ax=0的解空间的维数为2,求该方程组的通解.
,且齐次线性方程组Ax=0的解空间的维数为2,求该方程组的通解.
(7)已知线性方程组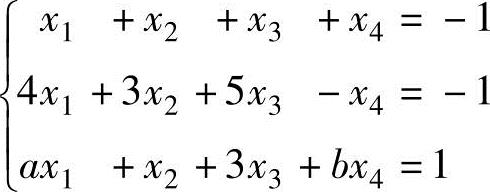
,
,有3个线性无关的解.(ⅰ)证明:该方程组的系数矩阵A的秩为2;(ⅱ)求a,b的值及该方程组的通解.(8)设线性方程组(Ⅰ):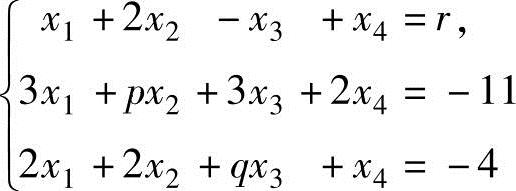 ,与(Ⅱ)
,与(Ⅱ)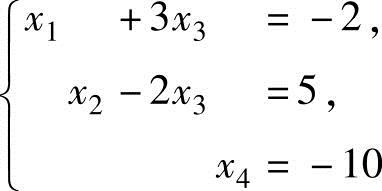 同解,试确定(Ⅰ)中p,q,r的值.
同解,试确定(Ⅰ)中p,q,r的值.
(9)设αi=(ai1,ai2,…,ain)T是n维实向量(i=1,2,…,r,r<n),且α1,α2,…,αr线性无关.已知β=(b1,b2,…,bn)T是齐次线性方程组
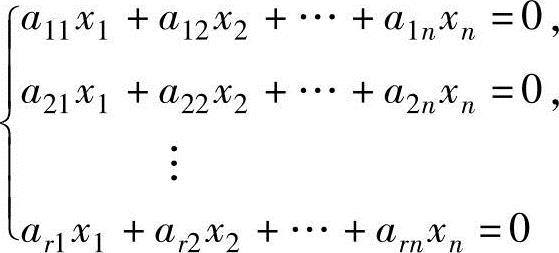
的非零解.试判定向量α1,α2,…,αr,β的线性相关性.
(10)设齐次线性方程组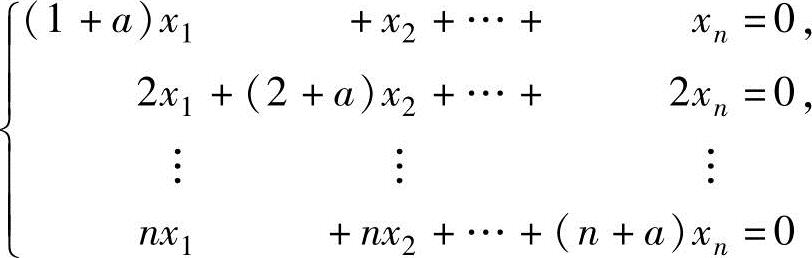 (n≥2),试问当a取何值时,该方程组有非零解,并求出其通解.
(n≥2),试问当a取何值时,该方程组有非零解,并求出其通解.
(11)判断方程组(Ⅰ)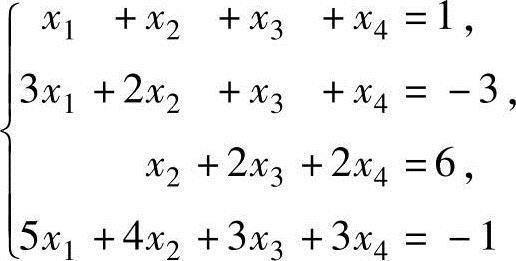 与(Ⅱ)
与(Ⅱ)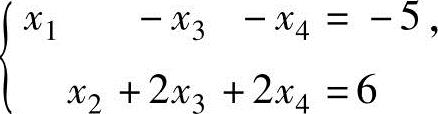 的同解性.
的同解性.
(12)已知齐次线性方程组(Ⅰ)的基础解系为
α1=(1,0,1,1)T,α2=(2,1,0,-1)T,α3=(0,2,1,-1)T.求(Ⅰ)与齐次线性方程组.
(Ⅱ)
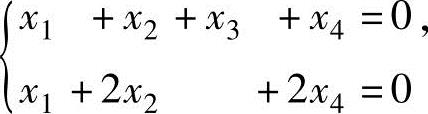
的所有公共解.
(13)设A是三阶矩阵,满足A=0,A+E3=0,trA=0,求A的特征值.
(14)设A是满足A3+A2+A=3En的n阶实对称矩阵,求A.
(15)设四阶矩阵A满足AAT=2E4,且A<1,求A的伴随矩阵A∗的两个特征值.
(16)设三阶矩阵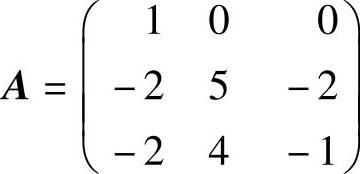 ,问A100是否能相似对角化?如果能相似对角化,写出这个对角矩阵.
,问A100是否能相似对角化?如果能相似对角化,写出这个对角矩阵.
(17)已知向量α=(1,k,1)T是矩阵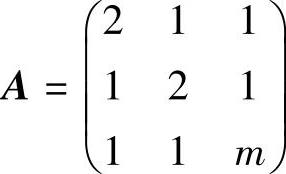 的逆矩阵A-1的特征向量,求常
的逆矩阵A-1的特征向量,求常
数k和m的值.
(18)已知三阶实对称矩阵A的一个特征值为2,其对应的特征向量为α=(1,2,-1)T,且A的主对角线上的元素全为零,求A.
(19)已知三阶实对称矩阵A的各行元素之和都为3,且α1=(-1,2,-1)T,α2=(0,-1,1)T是齐次线性方程组Ax=0的两个解向量,求A的全部特征值和特征向量.
(20)设矩阵A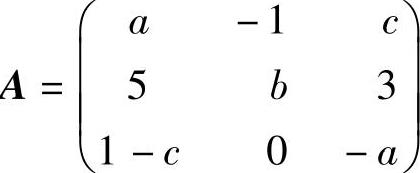 ,且A=-1,又设A∗有特征值λ0,它对应的特
,且A=-1,又设A∗有特征值λ0,它对应的特
征向量为α=(-1,-1,1)T,求a,b,c及λ0的值.
(21)设A,B都为n阶矩阵,证明:AB与BA有相同的特征值.
(22)设A,B都为n阶矩阵,且r(A)+r(B)<n,证明:A,B有公共的特征向量.
(23)已知二次型f(x1,x2,x3)=a(x21+x22+x23)+4x1x2+4x1x3+4x2x3经正交变换x=Py可化成标准形f=6y21,求常数a.
(24)设二次型f(x1,x2,x3)=xTAx=ax21+2x22-2x23+2bx1x3(b>0),其中,实对称矩阵A的特征值之和为1,特征值之积为-12.
(ⅰ)求常数a,b的值;
(ⅱ)利用正交变换x=Qy将f化为标准形,并写出正交矩阵Q.
(25)求二次型f(x1,x2,x3)=-4x1x2+2x1x3+2x2x3的秩与正惯性指数.
(26)用可逆线性变换x=Py将二次型f(x1,x2,x3)=x21+2x22-2x23+4x1x3化为规范形,并求可逆矩阵P.
(27)设二次型f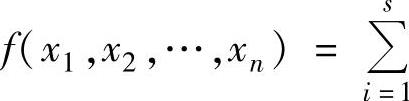 (ai1x1+ai2x2+…+ainxn)2,证明:f的秩为r(A),
(ai1x1+ai2x2+…+ainxn)2,证明:f的秩为r(A),
其中,A=(aij)s×n.
(28)设二次型f(x1,x2,x3)=x21+x22+x23-4x1x2-4x1x3+2ax2x3,经正交变换x=Qy(其中,x=(x1,x2,x3)T,y=(y1,y2,y3)T)化为标准形f=3y21+3y22+by23,求:
(ⅰ)常数a,b的值;
(ⅱ)正交矩阵Q;
(ⅲ)当xTx=2时,f(x1,x2,x3)的最大值.
(29)求参数t的取值范围,使得f(x1,x2,x3)=x21+4x22+4x23+2tx1x2-2x1x3+4x2x3为正定二次型.
(30)证明:二次型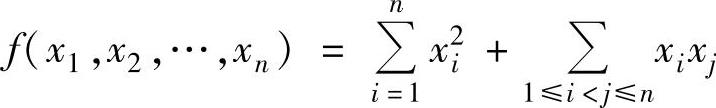 为正定二次型.
为正定二次型.
