向量组的标准正交化与正交矩阵
【主要内容】
1.向量内积的概念
（1）向量的内积
设n维向量α=（a1，a2，…，an）T，β=（b1，b2，…，bn）T，则称数
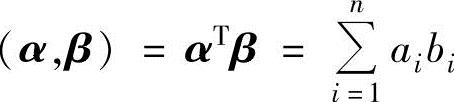
为α与β的内积.
向量内积的性质：设α，β，γ都是n维向量，则有
（ⅰ）（α，β）=（β，α）；
（ⅱ）（α+β，γ）=（α，γ）+（β，γ）；
（ⅲ）（kα，β）=（α，kβ）=k（α，β）（k为常数）；
（ⅳ）（α，α）≥0.称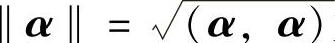
为向量α的模，且‖α‖=0的充分必要条件是
α=0.
（2）向量正交的概念
设α=（a1，a2，…，an）T，β=（b1，b2，…，bn）T都是n维非零向量，则当（α，β）=0，即a1b1+a2b2+…+anbn=0时，称α与β正交.
2.向量组的单位正交化
（1）单位正交向量组
设α1，α2，…，αm是向量组，如果它们是两两正交的非零向量，则称α1，α2，…，αm是正交向量组.
设α1，α2，…，αm是正交向量组，如果其中每个向量的模都为1，则称α1，α2，…，αm是单位正交向量组.
单位正交向量组的性质：设α1，α2，…，αm是单位正交向量组，则
（ⅰ）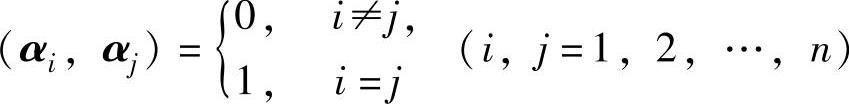
；
（ⅱ）α1，α2，…，αm线性无关，即r（α1，α2，…，αm）=m.
（2）向量组单位正交化方法（施密特单位正交化）
设向量组α1，α2，…，αm线性无关，则存在与该向量组等价的单位正交向量组ε1，ε2，…，εm.由α1，α2，…，αm到ε1，ε2，…，εm的过程称为α1，α2，…，αm的单位正交化.
线性无关向量组α1，α2，…，αm单位正交化的施密特方法如下：
（ⅰ）正交化：取
β1=α1，
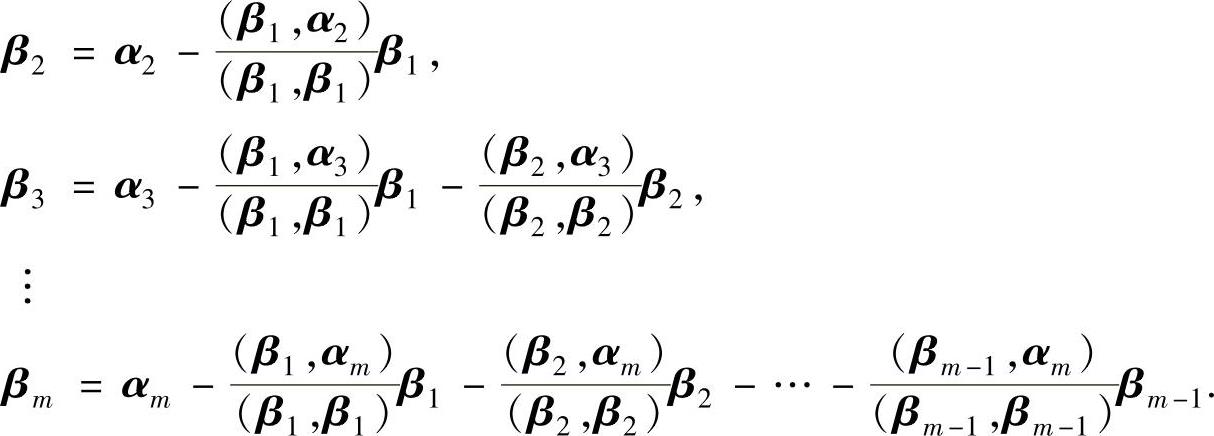
（ⅱ）单位化：
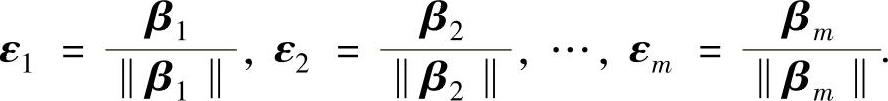
由此得到的ε1，ε2，…，εm是α1，α2，…，αm的单位正交化向量组.
3.正交矩阵
设A是n阶实矩阵.如果ATA=En，则称A是n阶正交矩阵.
正交矩阵的性质：设A，B都是n阶正交矩阵，则
（1）A可逆，且A-1=AT，从而有AAT=En；
（2）|A|=-1或1；
（3）AT与A-1都是正交矩阵；
（4）A的列向量组与行向量组都是单位正交向量组.
【典型例题】
例5.9.1 试将向量组α1=（2，0，1）T，α2=（0，1，0）T，α3=（1，0，2）T单位正交化.
精解 首先正交化：注意α1与α2正交，所以可取
β1=α1=（2，0，1）T，β2=α2=（0，1，0）T，
且由施密特正交化方法知
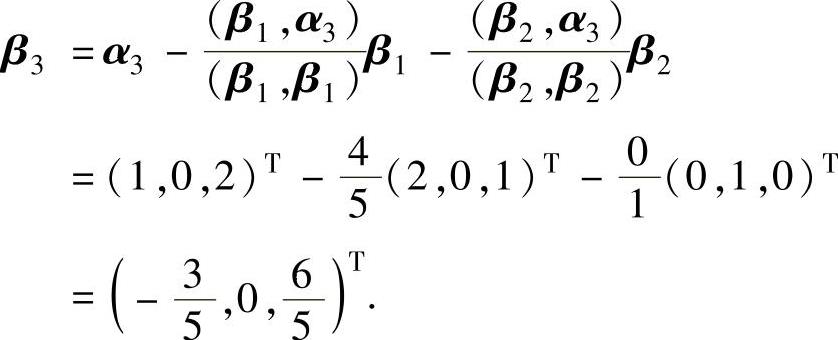
其次单位化：取
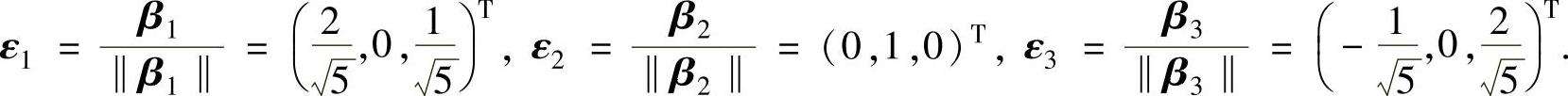
ε1，ε2，ε3即为α1，α2，α3的单位正交化向量组.
例5.9.2 设α1，α2，α3与β1，β2是两个线性无关的向量组，且（αi，βj）=0（i=1，2，3；j=1，2）.证明：向量组α1，α2，α3，β1，β2线性无关.
精解 用向量组线性无关的定义证明.
假设存在数λ1，λ2，λ3，μ1，μ2，使得
λ1α1+λ2α2+λ3α3+μ1β1+μ2β2=0，（1）即λ1α1+λ2α2+λ3α3=-μ1β1-μ2β2.（2）于是，（λ1α1+λ2α2+λ3α3，λ1α1+λ2α2+λ3α3）
=（λ1α1+λ2α2+λ3α3，-μ1β1-μ2β2）
=λ1μ1（α1，β1）-λ2μ1（α2，β1）-λ3μ1（α3，β1）-λ1μ2（α1，β2）-
λ2μ2（α2，β2）-λ3μ2（α3，β2）
=0（利用题设（αi，βj）=0，i=1，2，3；j=1，2）.
由此得到
λ1α1+λ2α2+λ3α3=0.（3）
由于α1，α2，α3线性无关，所以由式（3）得λ1=λ2=λ3=0.将它代入式（2）得
μ1β1+μ2β2=0.
由于β1，β2线性无关，所以μ1=μ2=0.
由上可知，当且仅当λ1=λ2=λ3=μ1=μ2=0时式（1）成立，所以α1，α2，α3，β1，β2线性无关.
例5.9.3 设A，B都是n阶正交矩阵，且|A|+|B|=0，求行列式|A+B|的值.
精解 利用正交矩阵的定义与性质计算行列式|A+B|.
由 A，B都是正交矩阵，知
AAT=En，BTB=En，所以
A+B=AEn+EnB=ABTB+AATB
=A（BT+AT）B=A（A+B）TB.
从而 |A+B|=|A||（A+B）T||B|=-|A|2|A+B|（利用|A|+|B|=0，即|B|=-|A|），
即 |A+B|（1+|A|2）=0.
由于 1+|A|2≠0，所以由上式得|A+B|=0.
例5.9.4 设A是实对称矩阵，B是实反对称矩阵，AB=BA，且A-B是可逆矩阵.证明：（A+B）（A-B）-1是正交矩阵.
精解 由题设知AT=A，BT=-B，从而由A-B可逆知A+B=（A-B）T可逆.从而由
[（A+B）（A-B）-1]T[（A+B）（A-B）-1]
=[（A-B）-1]T[（A+B）T（A+B）]（A-B）-1
=[（A-B）T]-1[（A-B）（A+B）]（A-B）-1
=（A+B）-1（A+B）（A-B）（A-B）-1
（由题设AB=BA知（A-B）（A+B）=（A+B）（A-B））
=[（A+B）-1（A+B）][（A-B）（A-B）-1]=En知（A+B）（A-B）-1是正交矩阵.