复合函数、反函数及隐函数的导数计算
【主要内容】
计算函数的导数的基础是求导基本公式和四则运算法则.
求导基本公式:
(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,
(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,
(4)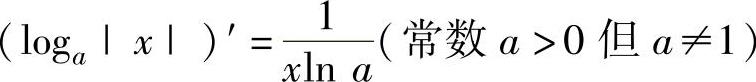 ,特别地,
,特别地,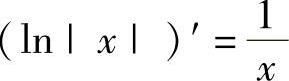 ,
,
(5)(sinx)′=cosx, (6)(cosx)′=-sinx,
(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,
(9)(secx)′=secxtanx, (10)(cscx)′=-cscxcotx,
(11)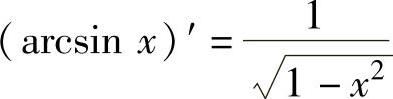 ,(12)
,(12)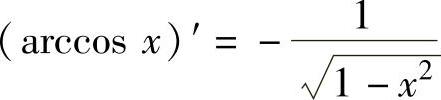 ,
,
(13)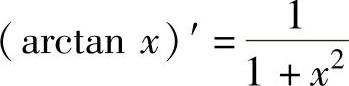 ,(14)
,(14)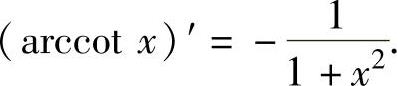
导数的四则运算法则:
设u(x),v(x)可导,则u(x)±v(x),u(x)v(x)以及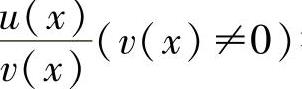 都可导,且
都可导,且
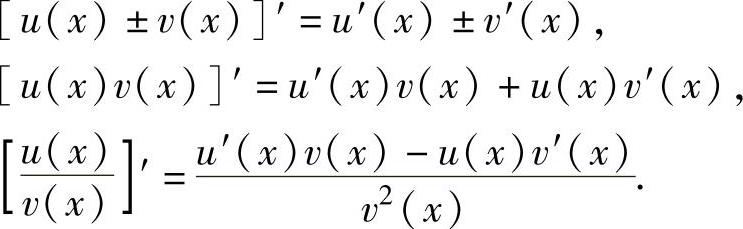
除此以外,还应掌握复合函数、反函数及隐函数的求导方法.
1.复合函数求导
设函数u=φ(x)在点x处可导,函数y=f(u)在点u=φ(x)处可导,则y=f(u)与u=φ(x)的复合函数y=f(φ(x))在点x处可导,且
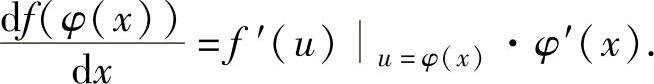
2.反函数求导
设函数x=φ(y)在某个区间内单调可导,且φ′(y)≠0,则它的反函数y=f(x)在对应区间内也可导,且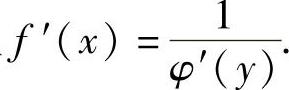
3.隐函数求导
设y=y(x)是由方程F(x,y)=0确定的隐函数,则所给方程两边对x求导(注意此时y
是x的函数)得到以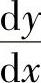 为未知数的方程,解此方程即得
为未知数的方程,解此方程即得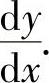
【典型例题】
例1.10.1 设函数f(x)=esinx,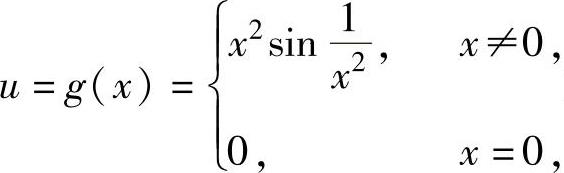 求
求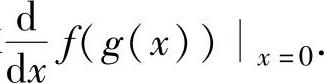
精解由复合函数求导法则得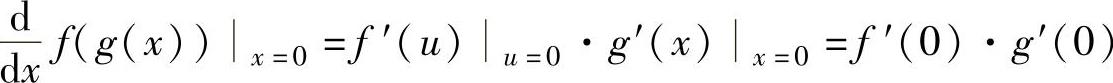 ,(1)
,(1)
其中,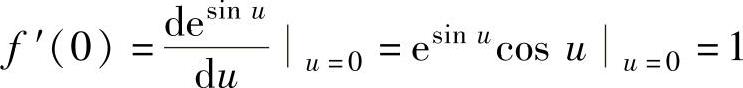 ,
,
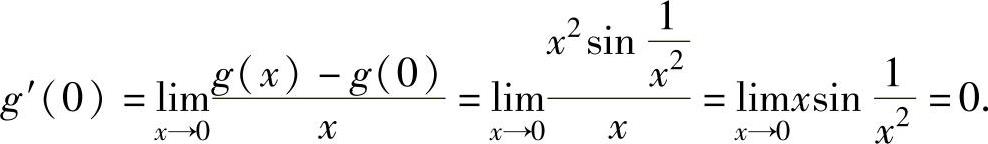
将它们代入式(1)得(https://www.daowen.com)
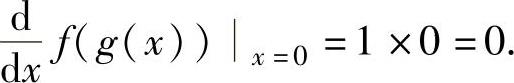
例1.10.2 求函数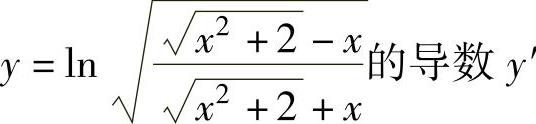 .
.
精解 先化简函数的表达式(例如,将真数的开方转换成对数的系数,将真数的分母有
理化),再求导.
由于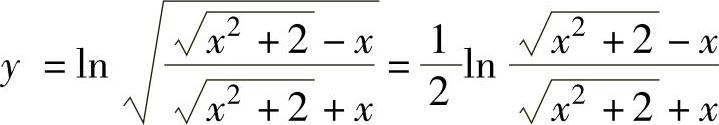
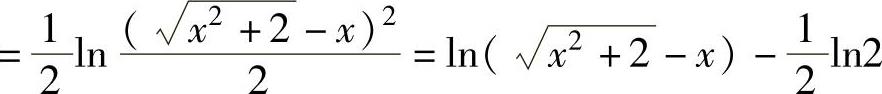 ,
,
所以,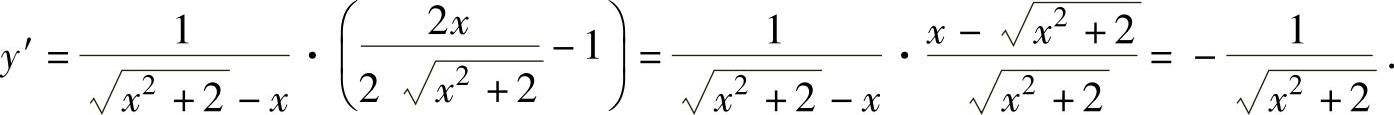
例1.10.3 设函数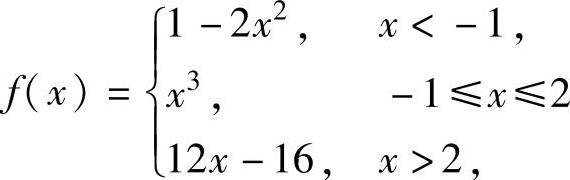 ,求y=f(x)的反函数y=φ(x)的导数φ′(x).
,求y=f(x)的反函数y=φ(x)的导数φ′(x).
精解 先确定φ(x)的表达式,然后计算φ′(x).
从y=f(x)中解出x得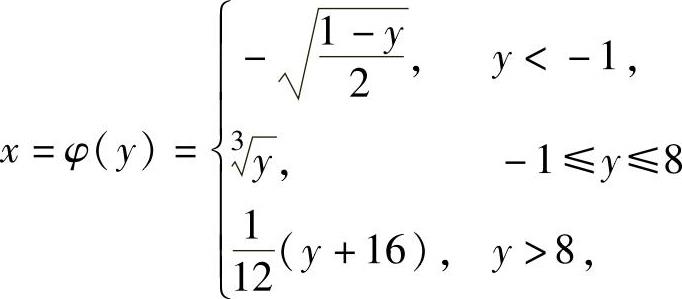 ,
,
所以y=f(x)的反函数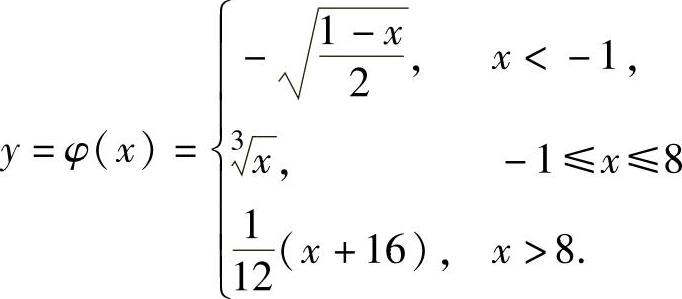 ,
,
当x<-1时,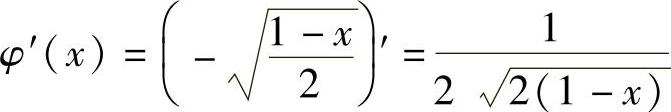 ;
;
当-1<x<8,但x≠0时,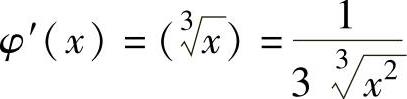 ;
;
当x>8时,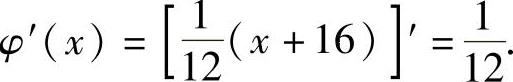
此外,由导数定义知,φ(x)在点x=-1,0处不可导,在点x=8处可导,且φ′(8)=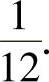
因此,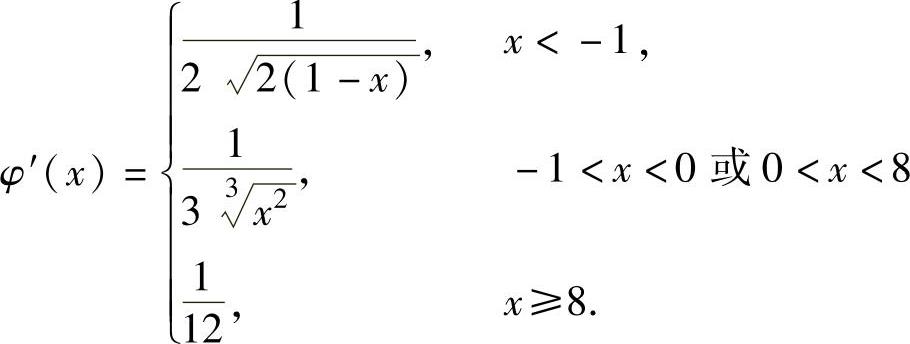 ,
,
注 在解题过程中不仅要注意φ(x)在点x=-1,8(分段点)处的可导性,还应注意φ(x)在点x=0处不可导.
例1.10.4 设函数y=f(x)由方程e2x+y-cos(xy)=e-1确定.求曲线y=f(x)在点(0,
1)处的切线方程.
精解 由隐函数求导方法算出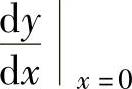 ,即可得到所求的切线方程.
,即可得到所求的切线方程.
所给方程两边对x求导得
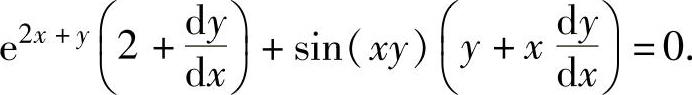
将x=0,y=1代入上式得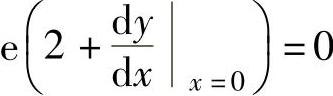 ,即
,即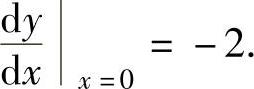
于是,曲线y=f(x)在点(0,1)处的切线方程为y-1=-2(x-0),即 y=-2x+1.
例1.10.5 求函数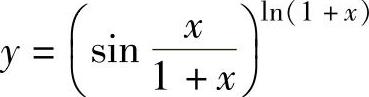 的导数.
的导数.
精解 当函数y=y(x)是幂指函数或由多个因子的积、商、乘方及开方组成时,往往采用取对数求导,即对y=y(x)的两边取对数后再求导.
所给函数是幂指函数,对其取对数得
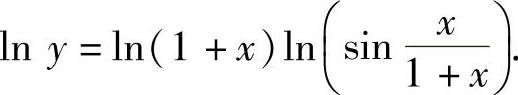
两边对x求导得
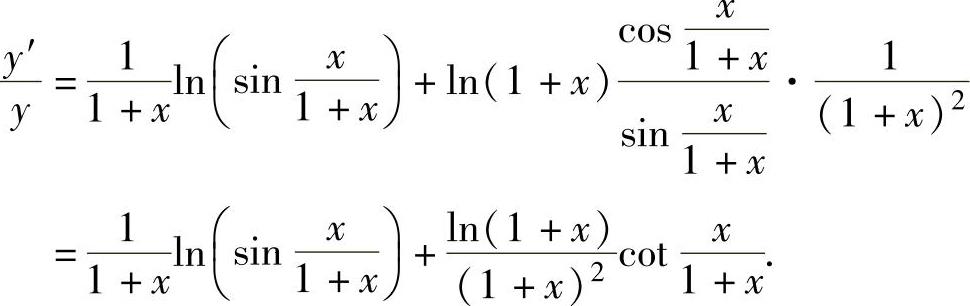
所以,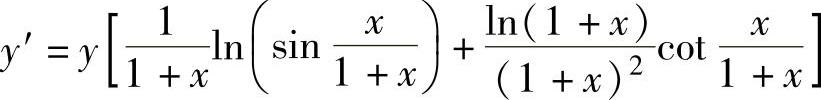
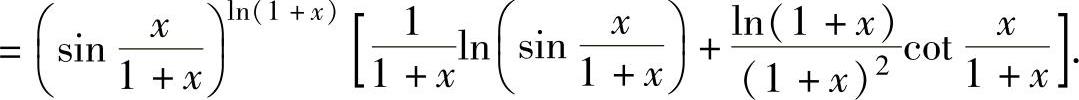
注 当y=y(x)时,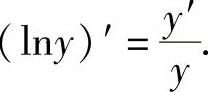 应记住这个公式.
应记住这个公式.
