函数最值的计算

十九 、函数最值的计算

【主要内容】

1.设函数f（x）在[a，b]上连续，则f（x）在[a，b]上必有最大值M与最小值m.它们可按以下步骤计算：

（1）算出f（x）在（a，b）内的所有可能极值点，记为x₁，x₂，…，x_n；

（2）比较f（x₁），f（x₂），…，f（x_n），f（a），f（b），其中最大者即为M，最小者即为m.

2.设函数f（x）在（a，b）内可导，且存在x₀∈（a，b），使得

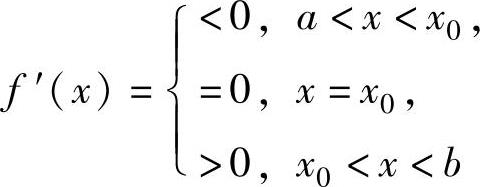
或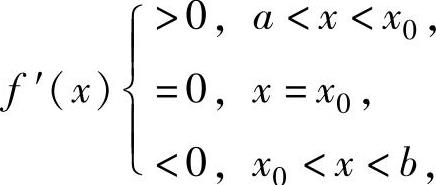

则f（x）在（a，b）内有最小值f（x₀），无最大值（有最大值f（x₀），无最小值）.这里的a，b可分别为-∞，+∞.

【典型例题】

例1.19.1 求函数f（x）=|x²-3x+2|在[-10，10]上的最大值和最小值.

精解 由于曲线y=f（x）容易画出，因此用画图方法求解本题.

由y=x²-3x+2=（x-1）（x-2）的图形直接可得y=|x²-3x+2|的图形如图1.19.1所示，由图可知f（x）在[-10，10]上的最小值为0（它在点x=1，2处取到），最大值为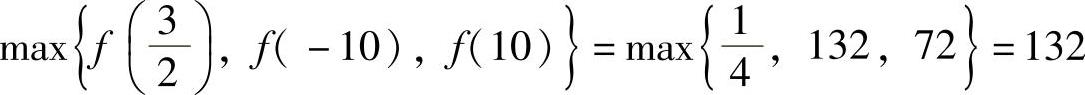（它在点x=-10处取到）.

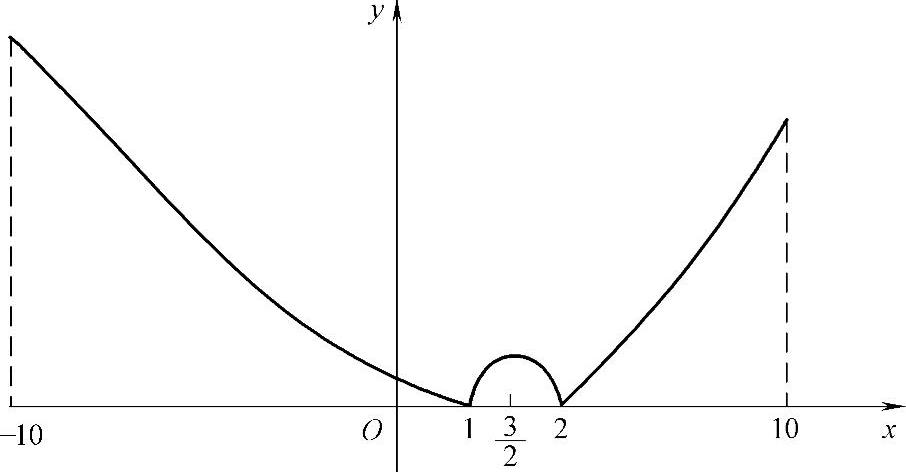
图 1.19.1

例1.19.2 设函数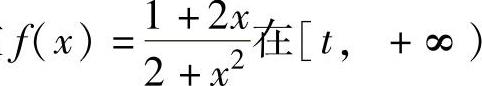上的最大值为M（t），求M（t）的表达式.

精解 用导数方法画出y=f（x）的概图，由此可得到M（t）的表达式.f（x）的定义域为（-∞，+∞），在其上可导且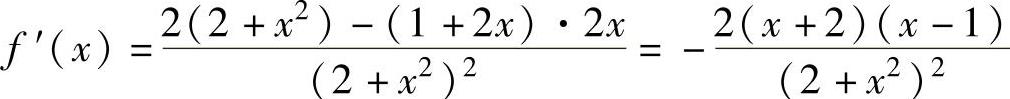，(https://www.daowen.com)

所以，f（x）的可能极值点为x=-2，1，据此列表如下：

由上表及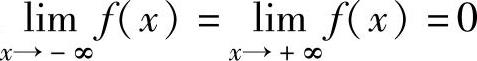知y=f（x）的概图如图1.19.2所示.由图可知

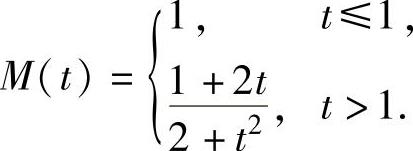
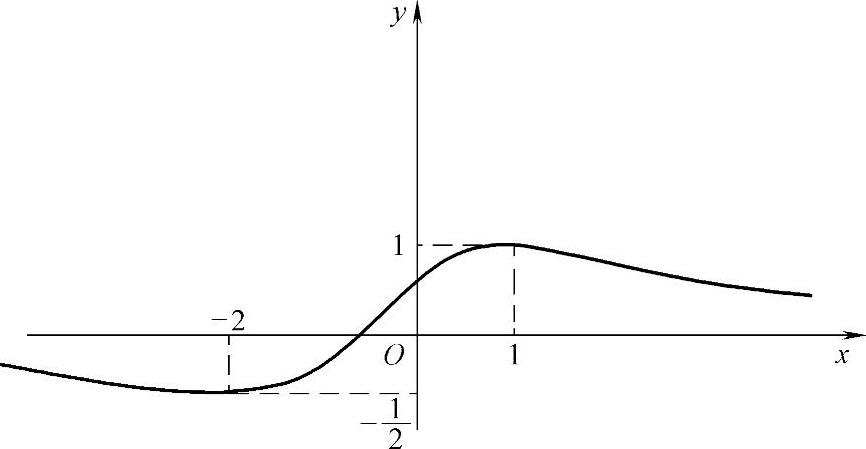
图 1.19.2

例1.19.3 设函数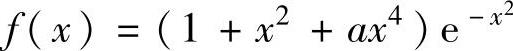，按常数a（a>0）的取值讨论f（x）在（-∞，+∞）上的最值.

精解 由于f（x）是偶函数，所以只要考虑a的取值与f（x）在[0，+∞）上取最大值的关系即可.

f（x）在[0，+∞）上可导且

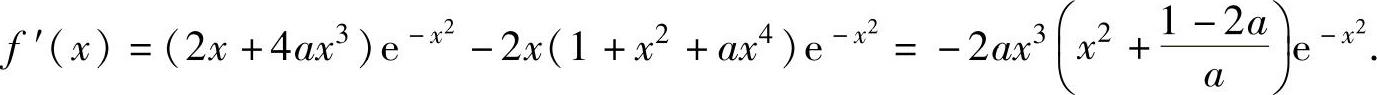
当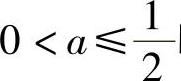时，f′（x）<0，x∈（0，+∞），所以f（x）在[0，+∞）上有最大值f（0）=

1.由于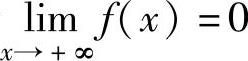，所以f（x）在[0，+∞）上无最小值.因此，f（x）在（-∞，+∞）上

有最大值f（0）=1，无最小值.

当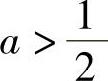时，对x∈（0，+∞）有

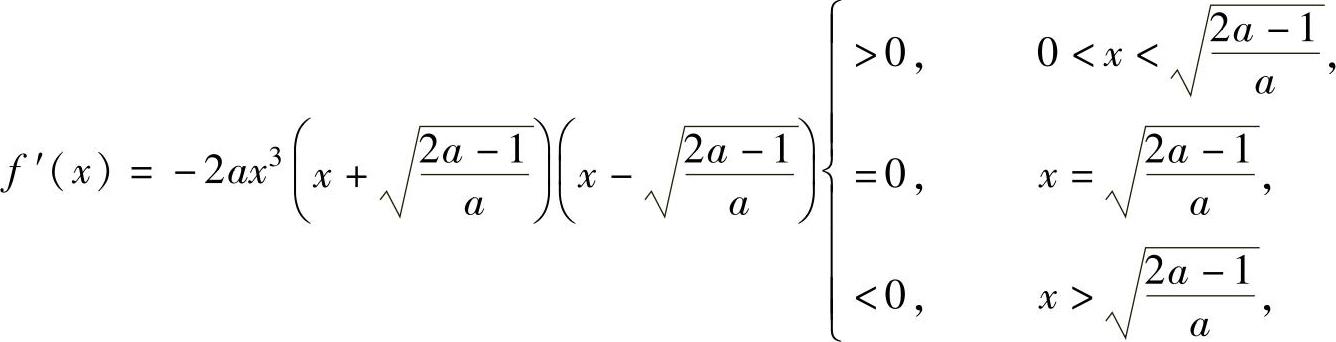
所以，f（x）在[0，+∞）上有最大值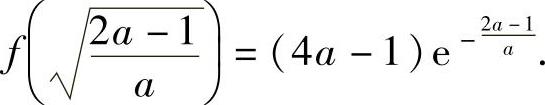此外，由于f（0）=1，而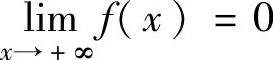知无最小值.因此，f（x）在（-∞，+∞）上有最大值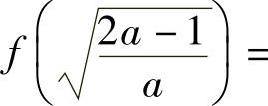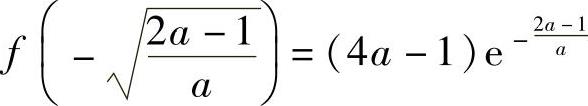，无最小值.