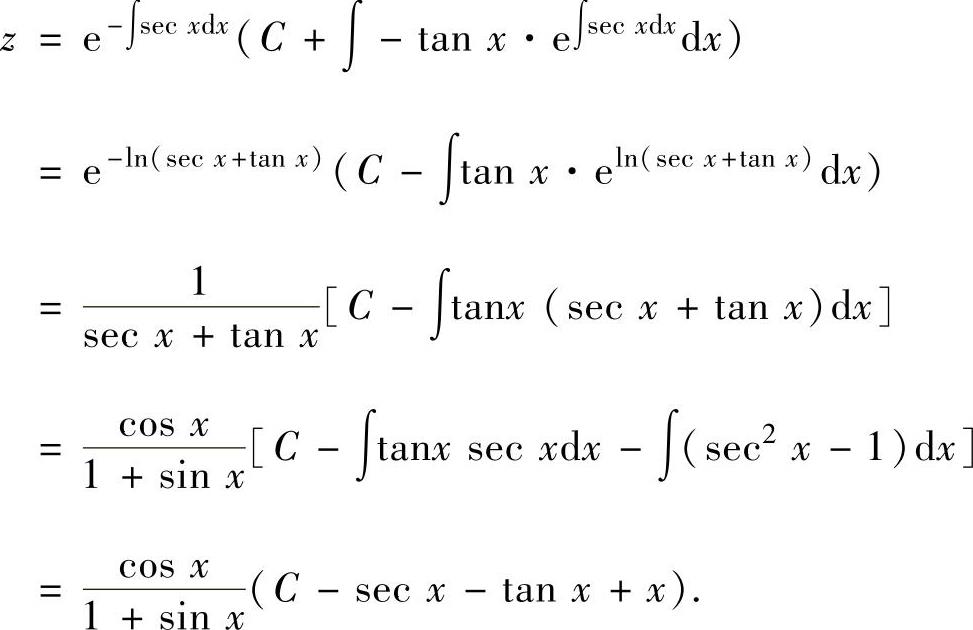一阶线性微分方程与伯努利方程

二 、一阶线性微分方程与伯努利方程

【主要内容】

1.一阶线性微分方程

形如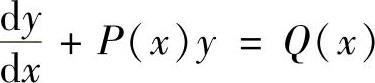（其中P（x），Q（x）是已知函数）的微分方程，称为一阶线性微

分方程，它的通解为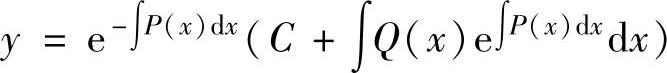（其中的不定积分都取一个原函数）.

2.伯努利方程

形如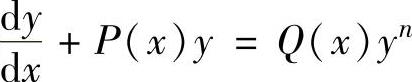（n≠0，1，P（x），Q（x）都是已知函数）的微分方程，称为伯

努利方程.

令z=y^1-n，伯努利方程转换成一阶线性微分方程

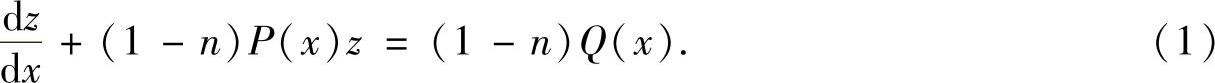
由式（1）的通解即可得到伯努利方程的通解.

【典型例题】(https://www.daowen.com)

例4.2.1求微分方程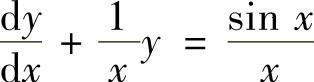的通解.

精解 所给微分方程是一阶线性微分方程，它的通解为

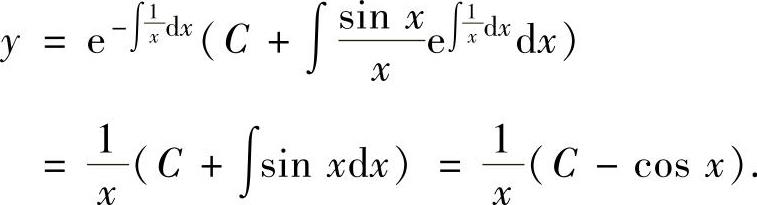
例4.2.2 求微分方程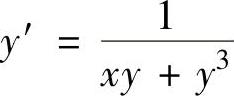的通解.

精解 所给的微分方程既不是一阶线性微分方程，又不是变量可分离微分方程和齐次微分方程，但是，如果把y看做自变量，x看做未知函数，则这个微分方程成为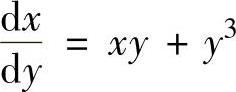，即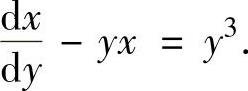（一阶线性微分方程）

它的通解为

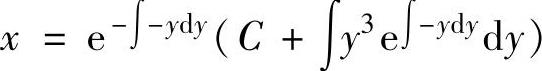
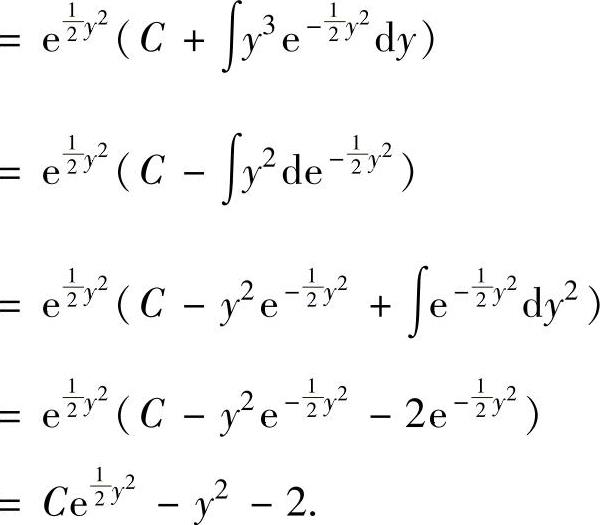
注 当所给的一阶微分方程y′=f（x，y）不是变量可分离微分方程、齐次微分方程、一阶线性微分方程、伯努利方程时，可以考虑交换自变量x与未知函数y，即将x作为未知函数，将y作为自变量.

例4.2.3 求微分方程3y′-ysecx=y⁴tanx的通解.

精解 由于所给微分方程可改写为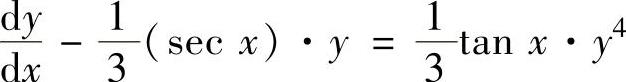（n=4的伯努利方程）.（1）令z=y^1-4=y^-3，则式（1）成为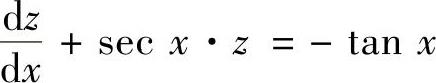（一阶线性微分方程）它的通解为