函数可导与导数的概念

八 、函数可导与导数的概念

【主要内容】

1.函数在点x₀处可导与导数的定义

设函数f（x）在点x₀的某个邻域内有定义.如果极限

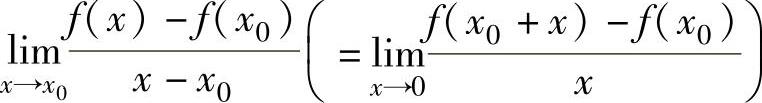
存在，则称f（x）在点x₀处可导，且称这个极限的值为f（x）在点x₀处的导数，记为f′（x₀）

或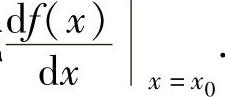

注 函数在点x₀处可导，必在点x₀处连续，但反之未必正确.

函数f（x）在点x0处可导的充分必要条件是f（x）在点x0处的左导数f-′（x0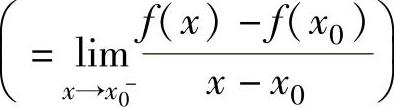）和右导数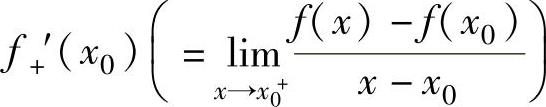都存在且相等.

注 当x₀是分段函数的分段点时，要判定f（x）在点x₀处是否可导或在计算f′（x₀）时，都需利用上述结论.

2.函数在开区间（a，b）内可导与闭区间[a，b]上可导的定义

如果f（x）在（a，b）内的每一点处都可导，则称f（x）在（a，b）内可导，并且可定义一个以（a，b）内每一点的导数为函数值的函数，称为f（x）在（a，b）内的导函数（简称导数），记为f′（x）.

如果f（x）在（a，b）内可导，且在点x=a与x=b处分别存在右导数f+′（a）和左导数f-′（b），则称f（x）在[a，b]上可导，并且可定义一个以[a，b]上每一点的导数（注意：点x=a处为右导数f+′（a），点x=b处为左导数f-′（b））为函数值的函数，称为f（x）在[a，b]上的导函数（简称导数），记为f′（x）.

【典型例题】

例1.8.1 设函数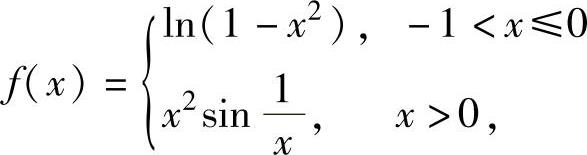

，

求f′（0）.

精解 由于x=0是f（x）的分段点，所以可通过计算f-′（0）与f+′（0）计算f′（0）.显然f（0）=0，所以，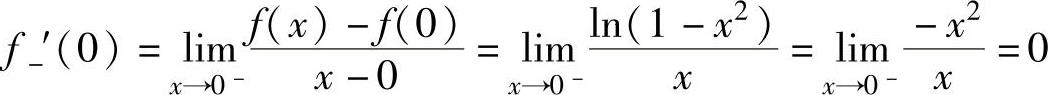

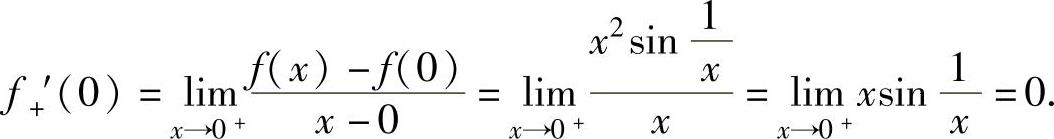
因此，f′（0）=0.

例1.8.2 设函数f（x）在（-∞，+∞）上有定义，且在[0，2）上f（x）=x（x²-4）.又设对任意x∈（-∞，+∞），f（x）满足f（x）=kf（x+2），求能够使f（x）在点x=0处可导的常数k.

精解 先写出f（x）在点x=0的某个邻域，例如（-2，2）内的表达式，然后由f+′（0）=f-′（0）可得k值.

由题设知，当x∈[0，2）时，f（x）=x（x²-4），于是当x∈（-2，0）时，有x+2∈（0，2），此时

f（x）=kf（x+2）=k（x+2）[（x+2）2-4]=kx（x+2）（x+4），

即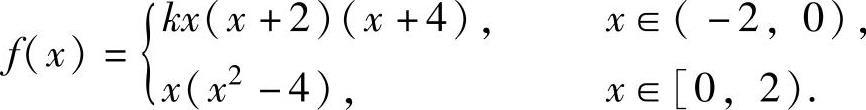

为使f（x）在点x=0处可导，k必须满足

f-′（0）=f+′（0），（1）

其中，，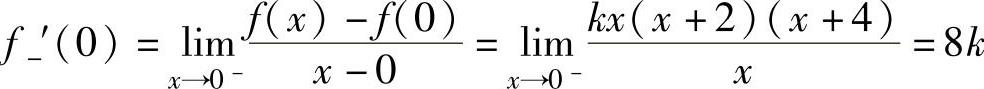

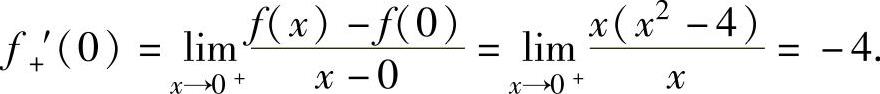
将它们代入式（1）得8k=-4，即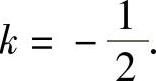

例1.8.3 设函数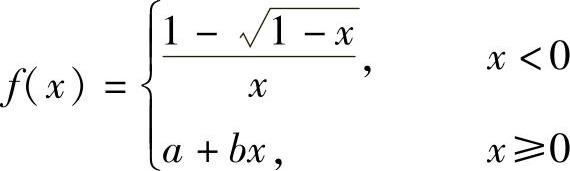，求能够使f（x）在点x=0处可导的常数，

a，b.

精解 由于要确定两个常数a，b，所以需要有两个方程，其中之一当然是f-′（0）=f+′（0）.另一个方程可以利用“可导蕴含连续”，即要使f（x）在点x=0处可导，必然要使f（x）在点x=0处连续.

由以上分析知，a，b必须满足

由式（1）得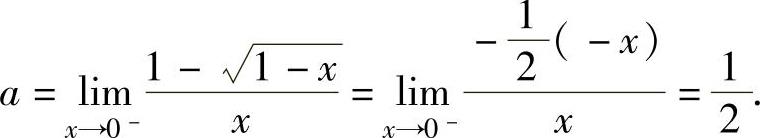（3）

将式（3）代入式（2）得

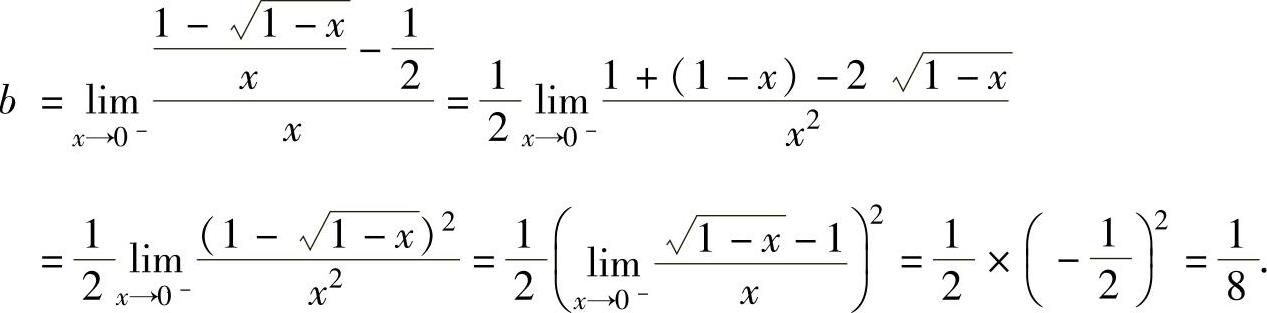
例1.8.4 设函数f（x）在点x=1处可导，且f（1）=0，f′（1）=2，求极限

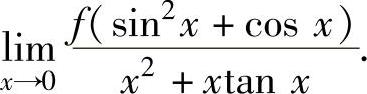
精解 由于f（sin²x+cosx）=f（1+（sin²x+cosx-1））-f（1）

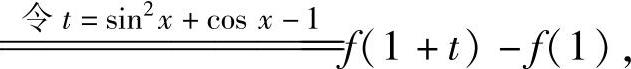
所以，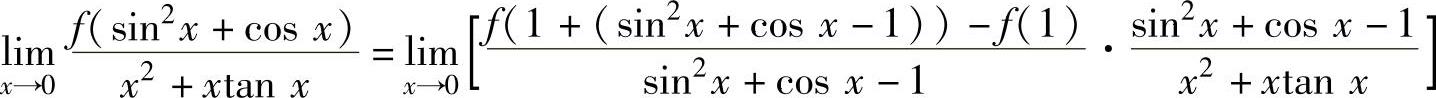

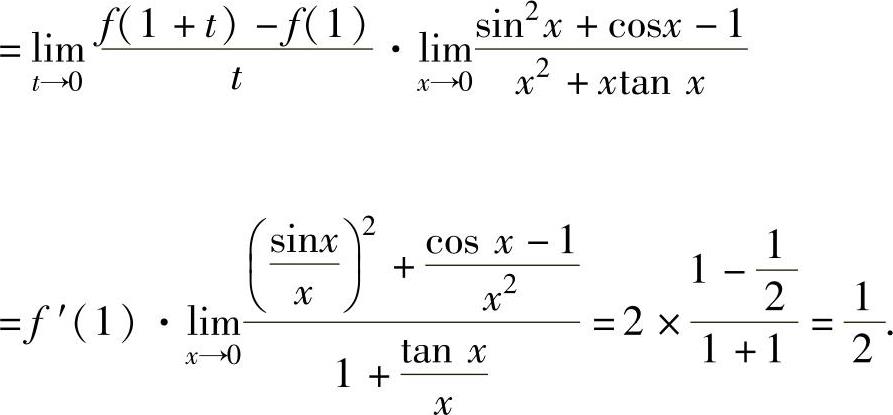
注 当已知函数f（x）在点x=a处的导数为f′（a）时，往往可利用导数定义计算形如

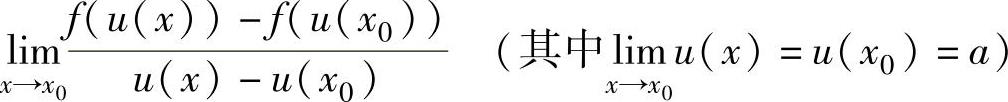
的极限.