练习题四
1.单项选择题
(1)设一阶非齐次线性微分方程y′+p(x)y=q(x)的两个不同特解为y1(x),y2(x),C为任意常数,则该微分方程的通解为( ).
A.C[y1(x)-y2(x)] B.y1(x)+C[y1(x)-y2(x)]
C.C[y1(x)+y2(x)] D.y1(x)+C[y1(x)+y2(x)]
(2)已知自变量x与函数y=y(x)在任意点x处的增量分别为Δx与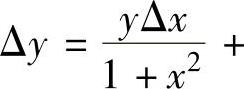
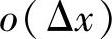 ,且y(0)=π,则y(1)=( ).
,且y(0)=π,则y(1)=( ).
A.2π B.π C.eπ4 D.πeπ4
(3)设二阶常系数非齐次线性微分方程y″-2y′+2y=exsinx,则它应具有的特解形式为( ).
A.ex·axsinx B.ex·axcosx
C.ex(acosx+bsinx) D.ex·x(acosx+bsinx)
(4)设y1(x),y2(x),y3(x)都是二阶线性微分方程
y″+P(x)y′+Q(x)y=f(x)
的特解,且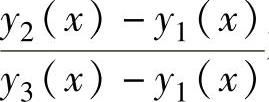 不恒为常数,则该微分方程的通解为( ).
不恒为常数,则该微分方程的通解为( ).
A.(1-C1-C2)y1(x)+C1y2(x)+C2y3(x)
B.C1y1(x)+C2y2(x)+C3y3(x)
C.C1y1(x)+C2y2(x)+y3(x)
D.C1[y2(x)-y1(x)]+C2[y3(x)-y1(x)]
(5)设y=y(x)是常系数齐次线性微分方程y″+py′+qy=0的通解,且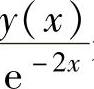 是以π为周
是以π为周
期的周期函数,则常数p,q的值为( ).
A.-4,-8 B.-4,8
C.4,-8 D.4,8
(6)设y1=xex+e2x,y2=xex+e-x是二阶常系线性微分方程y″+py′+qy=f(x)的两个特解,则p,q的值及该微分方程的通解为( ).
A.1,-2,C1e-x+C2e2x+xex
B.-1,-2,C1e-x+C2e2x+xex
C.1,-2,C1y1+C2y2
D.-1,-2,C1y1+C2y2
(7)已知曲线y=y(x)在原点处的切线垂直于直线x+2y=1,并且y(x)满足微分方程y″-2y′+5y=excos2x,则y(x)=( ).
A.ex(cos2x+sin2x-1) B.ex(sin2x-cos2x+1)
C.2xexsin2x D.2xexcos2x
(8)具有特解y1=e-x,y2=2xe-x及y3=3ex的三阶常系数齐次线性微分方程为().
A.y‴-y″-y′+y=0 B.y‴+y″-y′-y=0
C.y‴-6y″+11y′-6y=0 D.y‴-2y″-y′+2y=0
(9)设函数y=y(x)满足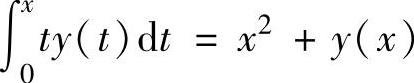 ,则y(x)=( ).
,则y(x)=( ).
A.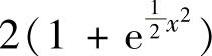 B.
B.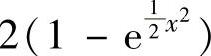
C.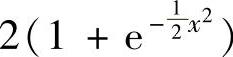 D.
D.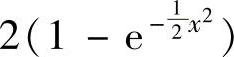
(10)设α为常数,则级数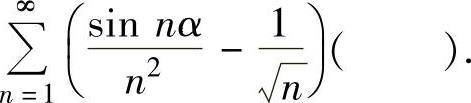
A.绝对收敛 B.条件收敛
C.发散 D.收敛性与α的取值有关
(11)已知级数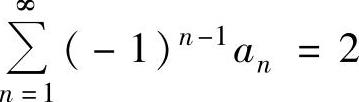 ,
,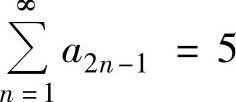 ,则级数
,则级数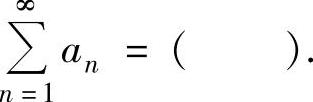
A.3 B.7 C.8 D.9
(12)下列命题中正确的是( ).
A.若级数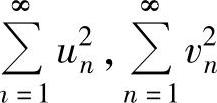 都收敛,则级数
都收敛,则级数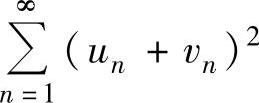 收敛
收敛
B.若级数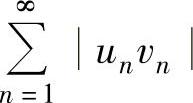 收敛,则级数
收敛,则级数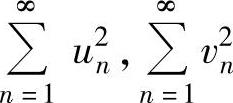 都收敛
都收敛
C.若正项级数发散,则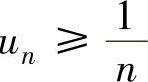 (n=1,2,…)
(n=1,2,…)
D.若级数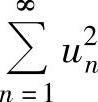 收敛,则级数
收敛,则级数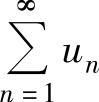 收敛
收敛
(13)设级数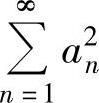 收敛,则级数
收敛,则级数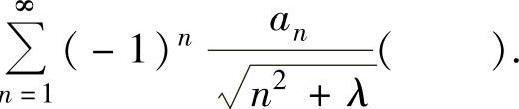
A.对任何正数λ都发散 B.对任何正数λ都条件收敛
C.对任何正数λ都绝对收敛 D.收敛性与正数λ有关
(14)级数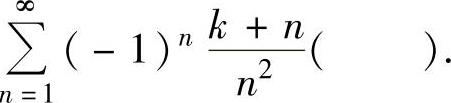
A.对任何k值绝对收敛 B.对任何k值条件收敛
C.对任何k值发散 D.收敛性与k值有关
(15)设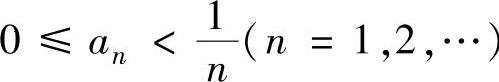 ,则下列级数中绝对收敛的是( ).(https://www.daowen.com)
,则下列级数中绝对收敛的是( ).(https://www.daowen.com)
A.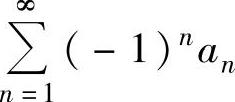 B.
B.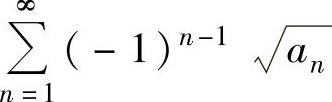
C.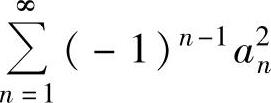 D.
D.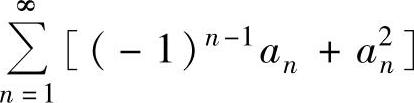
(16)下列命题正确的是( ).
A.若级数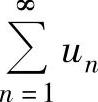 收敛,则级数
收敛,则级数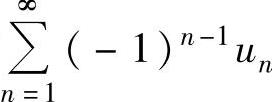 条件收敛
条件收敛
B.若级数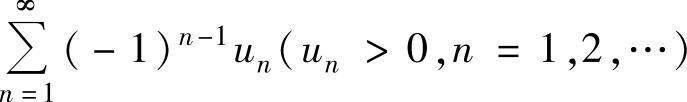 条件收敛,则级数
条件收敛,则级数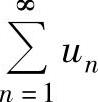 发散
发散
C.若级数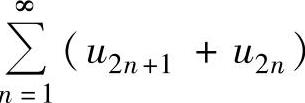 收敛,则级数
收敛,则级数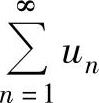 收敛
收敛
D.若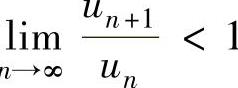 ,则级数
,则级数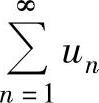 收敛
收敛
(17)设an>0(n=1,2,…).若级数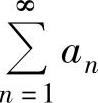 发散,级数
发散,级数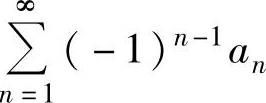 收敛,则下列结论正确的是( ).
收敛,则下列结论正确的是( ).
A.级数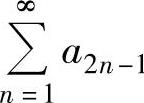 收敛,而级数
收敛,而级数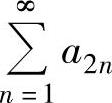 发散
发散
B.级数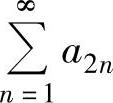 收敛,而级数
收敛,而级数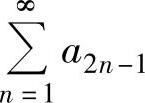 发散
发散
C.级数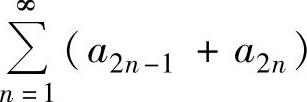 收敛
收敛
D.级数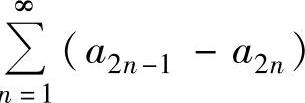 收敛
收敛
(18)设un≠0(n=1,2,3,…),且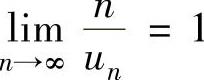 ,则级数
,则级数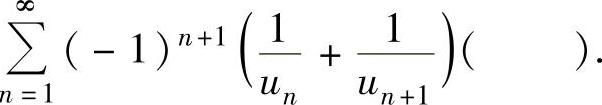
A.发散 B.绝对收敛
C.条件收敛 D.收敛性不能判断
(19)设幂级数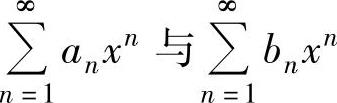 的收敛半径分别为
的收敛半径分别为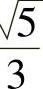 ,
,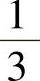 ,则幂级数
,则幂级数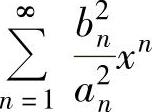 的收敛半径为( ).
的收敛半径为( ).
A.5B.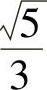 C.
C.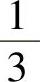 D.
D.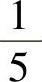
(20)幂级数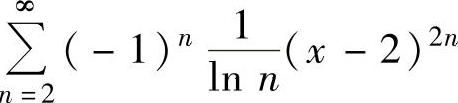 的收敛域为( ).
的收敛域为( ).
A.[1,3] B.(1,3] C.[1,3) D.(1,3)
(21)如果幂级数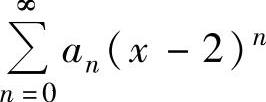 在点x=-2处收敛,则此幂级数在点x=5处( ).
在点x=-2处收敛,则此幂级数在点x=5处( ).
A.发散 B.条件收敛 C.绝对收敛 D.收敛性不能确定
2.解答题
(1)求微分方程y′+ycosx=(lnx)e-sinx的通解.
(2)求微分方程xy′+y-y2lnx=0的通解.
(3)求微分方程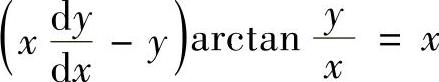 的通解.
的通解.
(4)求微分方程2yy′+2xy2=e-x2sinx的通解.
(5)求微分方程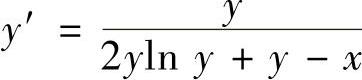 的通解.
的通解.
(6)求微分方程(3x2+2)y″=6xy′的解,使它在x→0时与ex-1是等价无穷小.
(7)设函数y(x)在(-∞,0]上连续,且满足
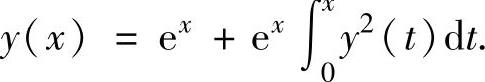
求y(x).
(8)设函数y(x)在[0,+∞)上有连续导数,且满足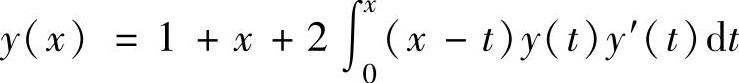 ,求y(x).
,求y(x).
(9)求微分方程y″+4y=x2+3sin2x+2cosx的通解.
(10)求微分方程y″+a2y=sinx的通解,其中,常数a>0.
(11)求极限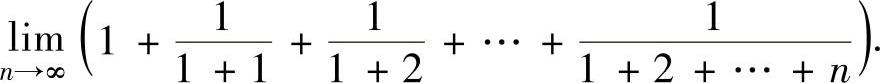
(12)设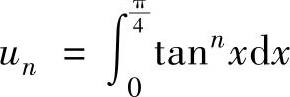 ,求级数
,求级数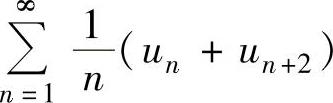 的和.
的和.
(13)判定级数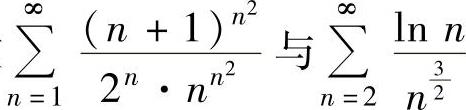 的收敛性.
的收敛性.
(14)判定下列级数的收敛性:
(ⅰ)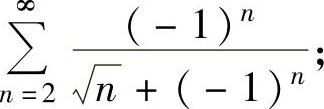
(ⅱ)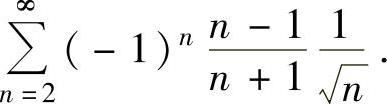
(15)求幂级数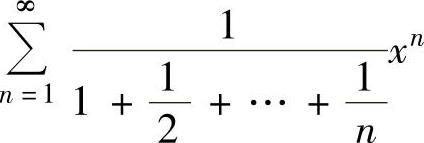 的收敛域.
的收敛域.
(16)求幂级数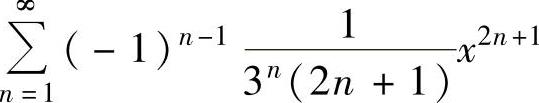 的收敛域与和函数.
的收敛域与和函数.
(17)求下列级数的和:
(ⅰ)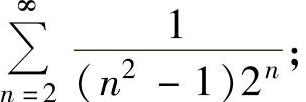
(ⅱ)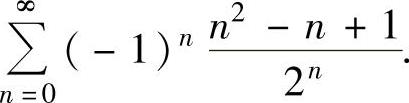
(18)将下列函数展开成关于x的幂级数:
(ⅰ)f(x)=ln(1-x-2x2);
(ⅱ)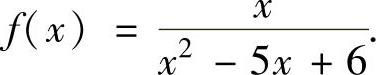
(19)将函数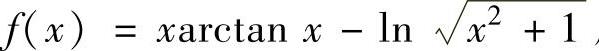 展开成关于x的幂级数.
展开成关于x的幂级数.
