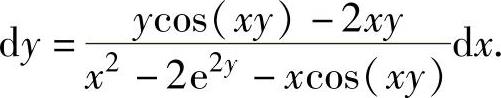函数微分的概念
【主要内容】
1.函数微分的定义
设函数y=f（x）在点x0的某个邻域内有定义.如果y在点x0处的增量
Δy=f（x0+Δx）-f（x0） （其中，Δx是自变量x在点x0处的增量）可表示为
Δy=AΔx+o（Δx）（其中，A与Δx无关，o（Δx）表示Δx→0时比Δx高阶的无穷小），则称y=f（x）在点x0处可微，称Δy的线性主部AΔx为y=f（x）在点x0处的微分，记为dy|x=x0（注意：函数y=f（x）在点x处的微分记为dy）.
如果函数f（x）在区间I的每个点处都可微，则称f（x）在I上可微.
2.函数微分的性质
（1）函数y=f（x）在点x处可微的充分必要条件是y=f（x）在点x处可导，此时，dy=f′（x）dx，其中dx=Δx（即自变量微分与自变量增量相等）.
（2）设函数y=f（u）可微，则不管u是自变量还是中间变量，都有
dy=f′（u）du.（微分形式不变性）
3.函数微分的应用
计算函数f（x）对函数u（x）的导数.
设f（x），u（x）都是可微函数，且u′（x）≠0，则
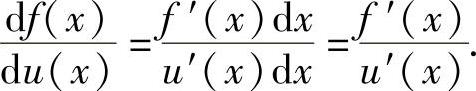
【典型例题】
例1.12.1 （单项选择题）设函数y=f（x）可导，且曲线y=f（x）在点（x0，y0）（其中，y0=f（x0））处的切线与直线y=2-x垂直，则当Δx→0时，dyx=x0是（）.
A.与Δx同阶但非等价的无穷小 B.与Δx等价的无穷小
C.比Δx高阶的无穷小 D.比Δx低阶的无穷小
精解 由题设算出f′（x0）即可判断应选哪个选项.
由曲线y=f（x）在点（x0，y0）处的切线与直线y=2-x垂直可知
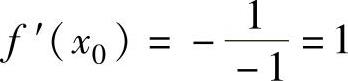
所以，dy|x=x0=f′（x0）Δx=Δx，即Δx→0时，dy|x=x0是与Δx等价的无穷小.
因此本题选B.
例1.12.2 设函数f（x）可导，且对函数y=f（x2），当自变量x在点x=-1处的增量Δx=-0.1时，相应的函数增量Δy的线性主部为0.1，求f′（1）.
精解 设Δy为可导函数φ（x）在点x0处的增量，则它的线性主部为φ′（x0）Δx.
于是根据题设有
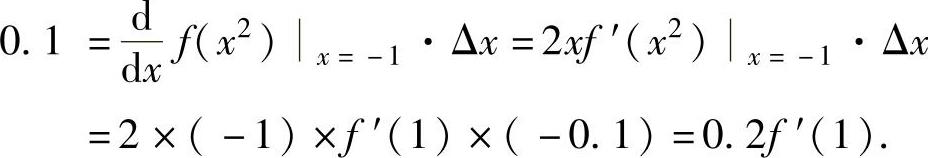
所以，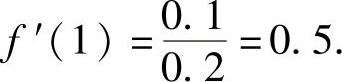
例1.12.3 设函数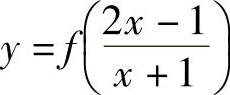
，且
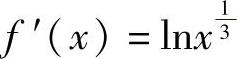，求dy.
精解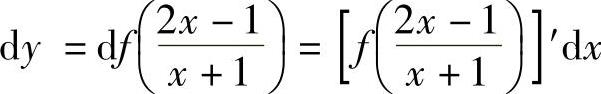
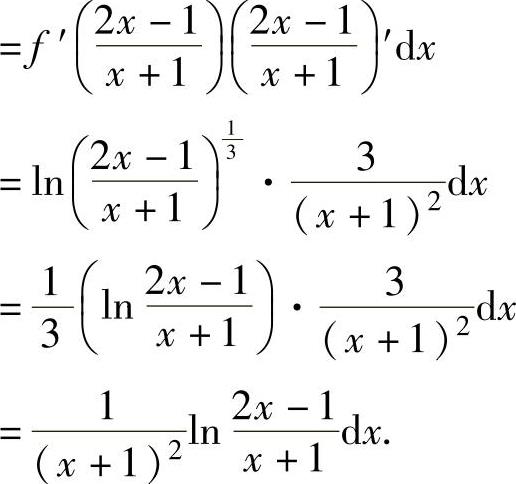
例1.12.4 设函数y=y（x）是由方程x2y-e2y=sin（xy）确定，求dy.精解 利用微分形式不变性，对所给方程两边求微分得d（x2y）-de2y=dsin（xy），
即2xydx+x2dy-2e2ydy=cos（xy）（ydx+xdy）.
合并同类项得[x2-2e2y-xcos（xy）]dy=[ycos（xy）-2xy]dx，所以，