不定积分的分部积分法

二 、不定积分的分部积分法

【主要内容】

不定积分的分部积分法就是利用公式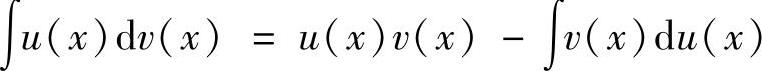（其中，

u（x），v（x）都具有连续的导数），将不定积分如果

∫v（x）du（x）比较容易计算，则由上述公式就可算得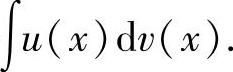

注 用分部积分法计算不定积分∫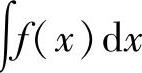时，应将它表示成∫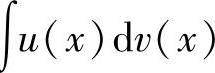的形式，即

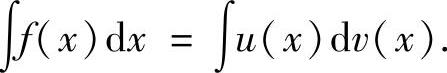
关于如何选择u（x），应遵循以下两个原则：

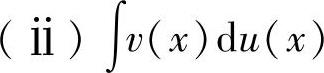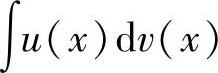（ⅰ）容易确定v（x），它是f（x）中除去u（x）后的剩余部分的一个原函数；较容易计算.

具体地，如果f（x）是对数函数或反三角函数时，则取u（x）=f（x）；如果f（x）是幂函数与三角函数或指数函数之积时，则取u（x）为幂函数；如果f（x）是幂函数与反三角函数或对数函数之积时，则取u（x）为反三角函数或对数函数；如果f（x）是指数函数与三角函数之积时，可取u（x）为指数函数或三角函数.

【典型例题】

例2.2.1 求不定积分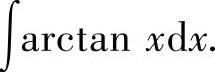

精解 由于被积函数是反三角函数，所以取u（x）=arctanx，于是由dv（x）=dx得v（x）=x.因此由分部积分法得

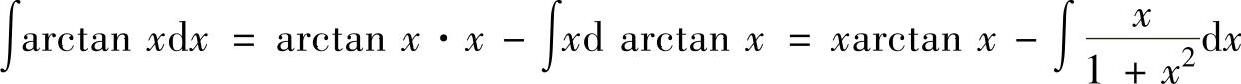
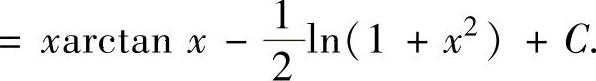
例2.2.2 求不定积分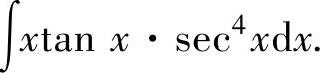

精解 由于被积函数是幂函数与三角函数之积，所以取u（x）=x，于是由

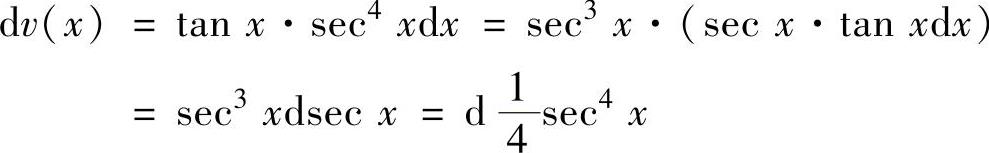
得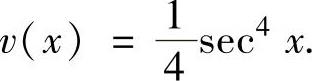因此由分部积分法有

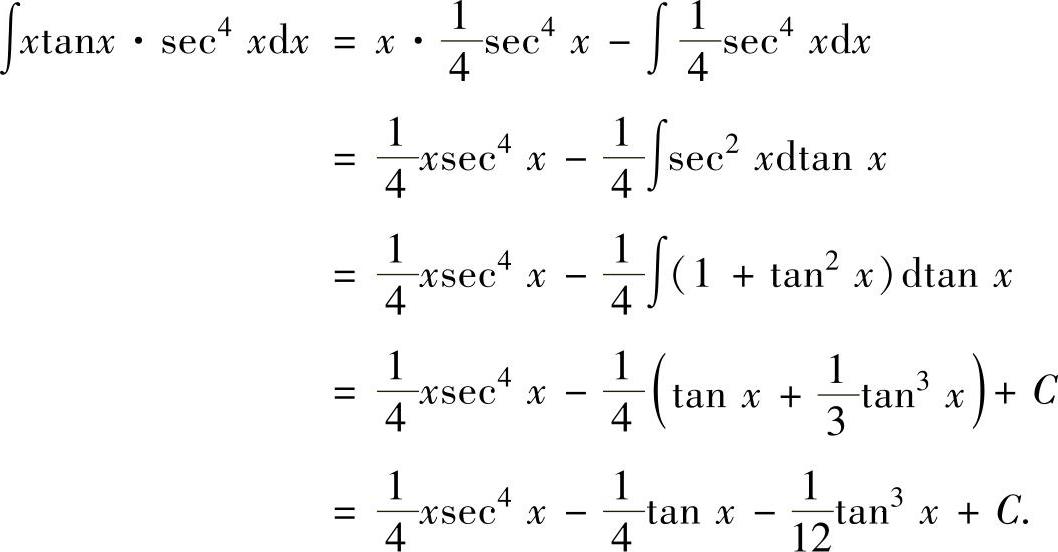
例2.2.3 求不定积分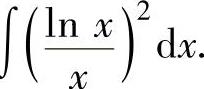

精解 由于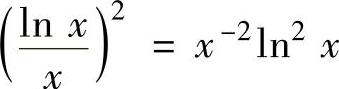是幂函数与对数函数之积，所以取u（x）=ln²x，于是由dv（x）=x^-2dx=d（-x^-1）得v（x）=-x^-1.因此由分部积分法有

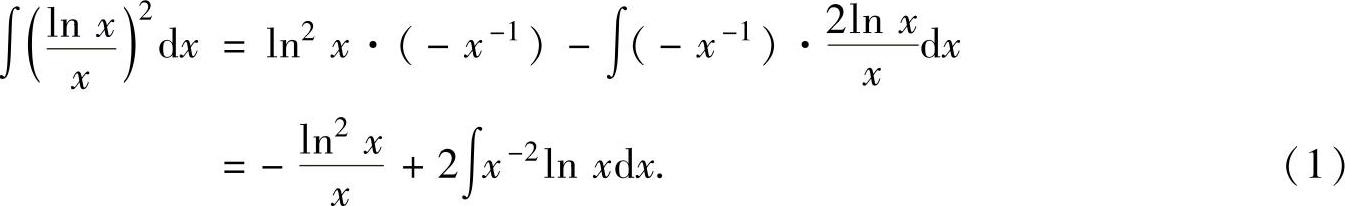
由于式（1）中不定积分的被积函数仍是幂函数与对数函数之积，所以取u₁（x）=lnx，于是由dv₁（x）=x^-2dx=d（-x^-1）得v₁（x）=-x^-1.因此由分部积分法有(https://www.daowen.com)

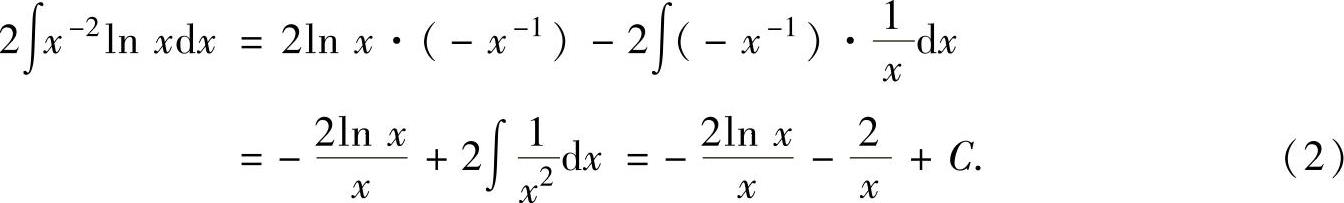
将式（2）代入式（1）得

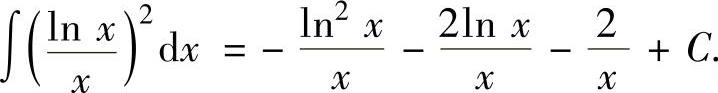
例2.2.4 求不定积分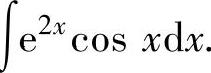

精解 由于被积函数是指数函数与三角函数之积，所以取u（x）=e^2x，于是由dv（x）=cosxdx=dsinx得v（x）=sinx.因此由分部积分法有

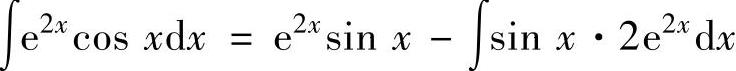
今后在计算过程中不必详写u（x）与v（x）的选取与计算，因此上述计算可直接写为

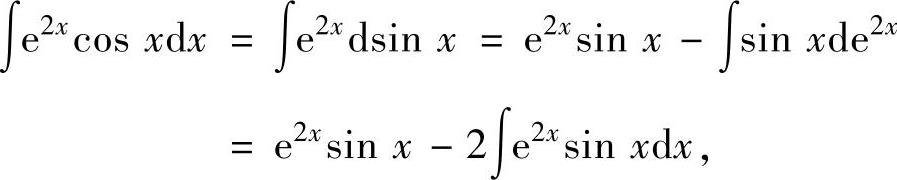
其中，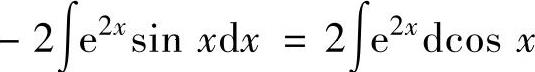

将式（2）代入式（1）得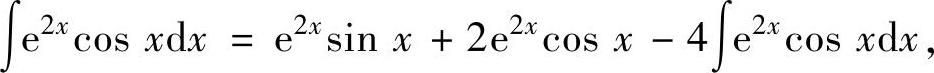

即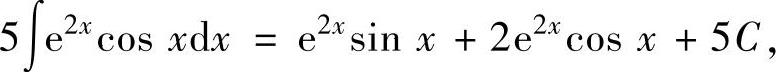

所以，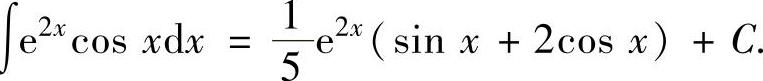

例2.2.5 设函数f（x）有一个原函数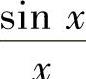，求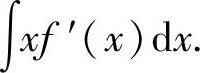

精解 本题可用分部积分法计算.

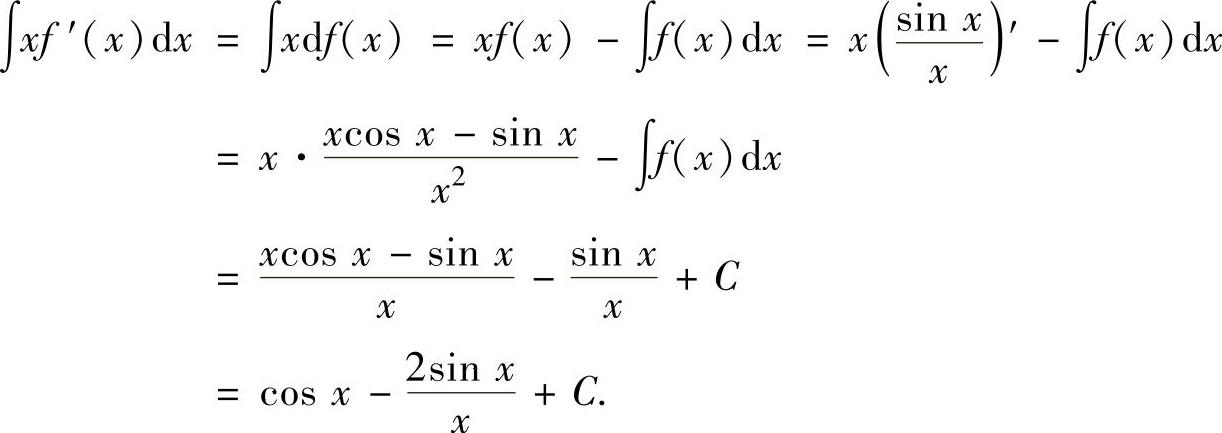
例2.2.6 求不定积分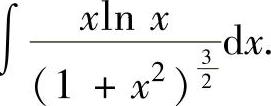

精解 由于被积函数中含有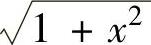，所以作变量代换x=tant后再进行计算.

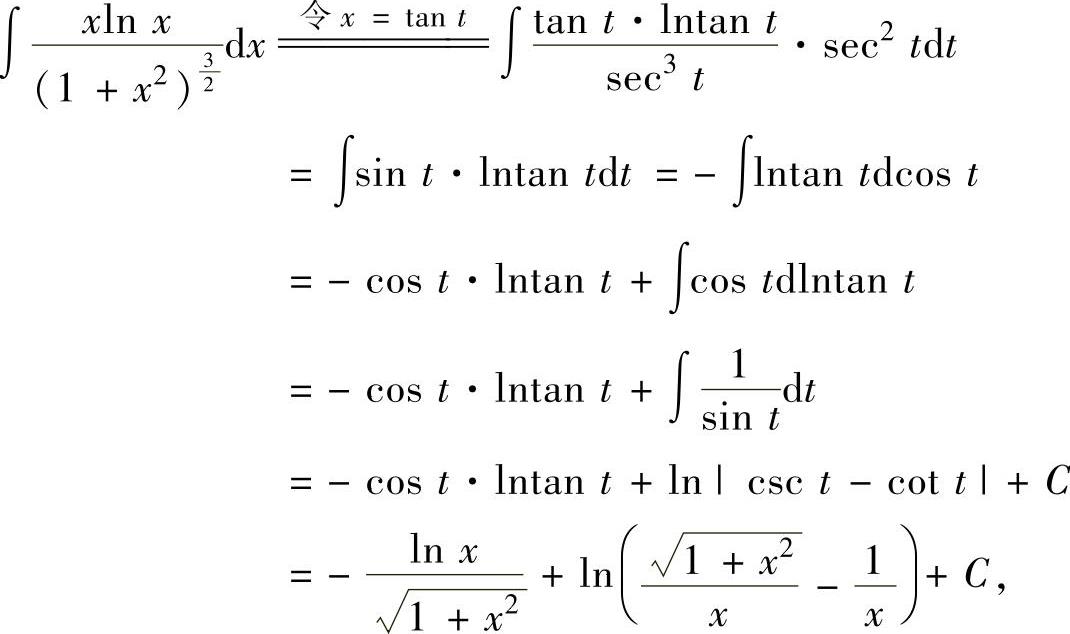
其中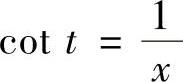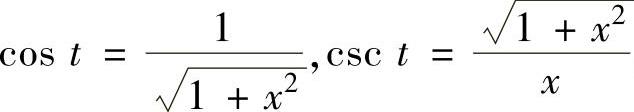，，这些都可从图

2.2.6中得到.

注 本题的不定积分是结合换元积分法与分部积分法算出来的.这种处理方法在不定积分的计算中是常会出现的，应予以注意.

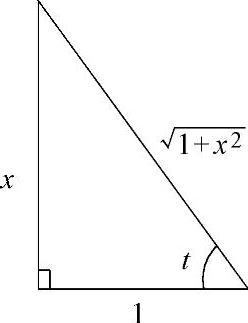
图 2.2.6