首页> 图书频道> 理学> 数学物理化学

矩阵的加法、数乘、乘法、转置运算及分块矩阵

2025年09月26日
版权
三 、矩阵的加法 、数乘 、乘法 、转置运算及分块矩阵

【主要内容】

1.矩阵的概念

由m×n个数aij（i=1，2，…，m；j=1，2，…，n）排成的m行n列的矩形表

978-7-111-46245-3-Part02-25.jpg

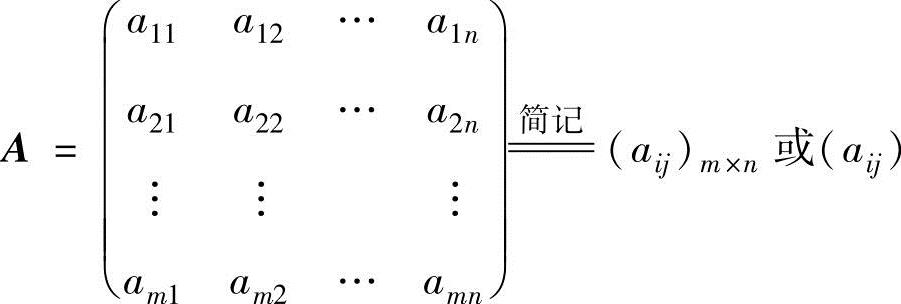
称为m×n矩阵，aij称为A的第i行第j列的元素（i=1，2，…，m；j=1，2，…，n）.当m=n时称A为n阶矩阵（或方阵），记它的行列式为|A|.

常见的特殊矩阵有：

（1）零矩阵.所有元素都为零的m×n矩阵称为m×n零矩阵，记为Om×n或O.

（2）单位矩阵.主对角线上元素都为1而其他元素都为零的n阶矩阵，称为n阶单位矩阵，记为En或E.

（3）对角矩阵.除主对角线上元素之外，所有元素都为零的n阶矩阵，称为n阶对角矩阵.

（4）对称矩阵与反对称矩阵.关于主对角线对称的元素彼此相等（或互为相反数）的n阶矩阵称为n阶对称矩阵（或n阶反对称矩阵）.

2.矩阵的加法、数乘与转置运算

（1）加法

设矩阵A=（aij）m×n，B=（bij）m×n，则由A，B产生A+B=（aij+bij）m×n的运算，称为矩阵的加法运算，简称加法.

加法性质：设矩阵A=（aij）m×n，B=（bij）m×n，C=（cij）m×n，则

A+B=B+A，（A+B）+C=A+（B+C），

A+Om×n=A，A+（-A）=Om×n（其中，-A=（-aij）m×n）.

（2）数乘

设矩阵A=（aij）m×n，k为常数，则由A产生kA=（kaij）m×n的运算，称为矩阵的数乘运算，简称数乘.

数乘的性质：设A=（aij）m×n，B=（bij）m×n，k，l是数，则

1·A=A，（k·l）A=k（lA）=l（kA），

k（A+B）=kA+kB，（k+l）A=kA+lA，

|kM|=kn|M|（M是n阶矩阵）.

（3）转置

设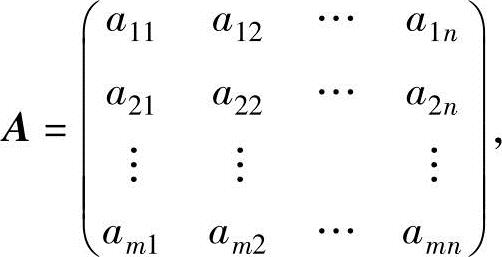978-7-111-46245-3-Part02-26.jpg则由A产生

978-7-111-46245-3-Part02-27.jpg

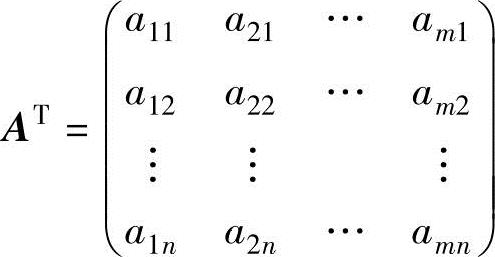
的运算称为矩阵

的转置运算，简称转置，称AT为A的转置矩阵.

设A是n阶矩阵，则A为对称矩阵（反对称矩阵）的充分必要条件是AT=A（AT=-A）.

转置的性质：设A，B都是m×n矩阵，则

（AT）T=A， （A+B）T=AT+BT， （kA）T=kAT，

|MT|=|M|（M是n阶矩阵）.

3.矩阵的乘法运算与乘幂

（1）设矩阵A=（aij）m×l，B=（bij）l×n，则由A，B产生

978-7-111-46245-3-Part02-28.jpg

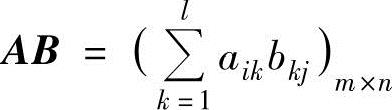
的运算称为A，B的乘法运算，简称乘法.

乘法的性质：设A，A1是m×l矩阵，B，B1是l×n矩阵，C是n×s矩阵，k是数，则

（AB）C=A（BC），

（A+A1）B=AB+A1B， A（B+B1）=AB+AB1，

（kA）B=A（kB）=k（AB），

（AB）T=BTAT，

|M1M2|=|M1||M2|（M1，M2都是n阶矩阵）.

（2）n阶矩阵的乘幂设A是n阶矩阵，则由A产生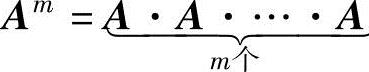978-7-111-46245-3-Part02-29.jpg的运算称为矩阵的乘幂运算，称Am

是A的m次乘幂，特别地，定义A0=En.

乘幂运算的性质：设A是n阶矩阵，k，l是非负整数，则

Ak·Al=Ak+l， （Ak）l=Akl.

4.分块矩阵

用若干条纵线和横线将矩阵A分成一些小块（小矩阵），以这些小块为“元素”的矩阵称为A的分块矩阵（注意A的分块矩阵与A相等）.

分块矩阵也有矩阵所具有的各种运算，只要把各小块看做元素即可，但需要注意的是各小块（即小矩阵）进行运算时，必须符合运算规则.

常见的分块矩阵运算有：

设

978-7-111-46245-3-Part02-30.jpg

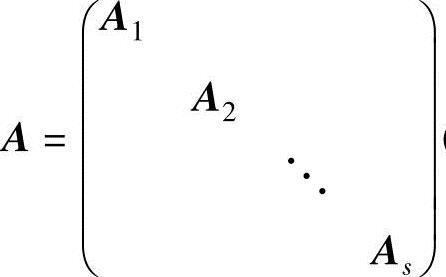
（其中，A1，A2，…，As都是方阵），

则

978-7-111-46245-3-Part02-31.jpg

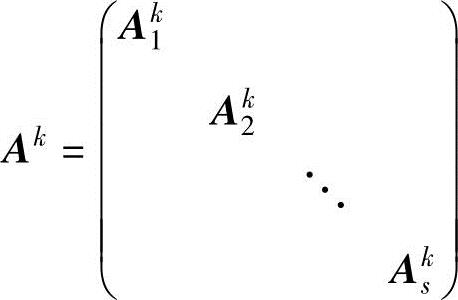
（k是非负整数），|A|=|A1||A2|…|As|.

设

978-7-111-46245-3-Part02-32.jpg

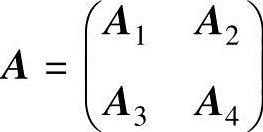
（其中，A1，A2分别是m1×s1，m1×s2矩阵，A3，A4分别是m2×

s1，m2×s2矩阵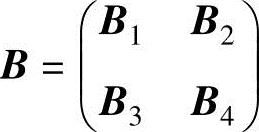）978-7-111-46245-3-Part02-33.jpg（其中，B1，B3分别是s1×n1，s2×n1矩阵，B2，B4分别是s1×n2，s2×n2矩阵），

则有

978-7-111-46245-3-Part02-34.jpg

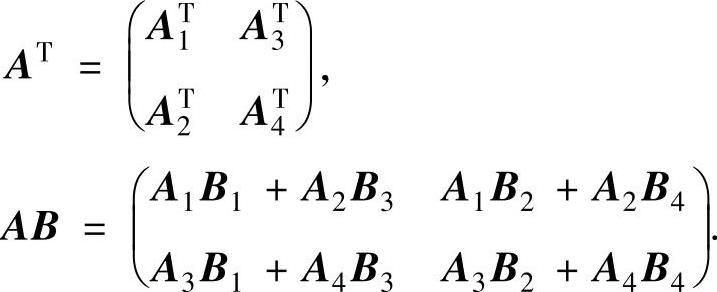
【典型例题】

例5.3.1 已知α=（1 2 3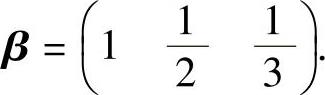），978-7-111-46245-3-Part02-35.jpg记A=αTβ，求An.

精解 由于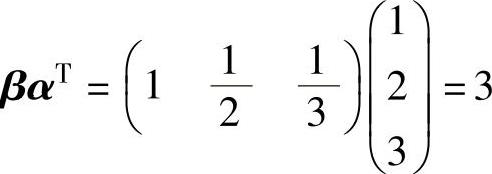978-7-111-46245-3-Part02-36.jpg，所以利用矩阵乘法性质计算An.

978-7-111-46245-3-Part02-37.jpg

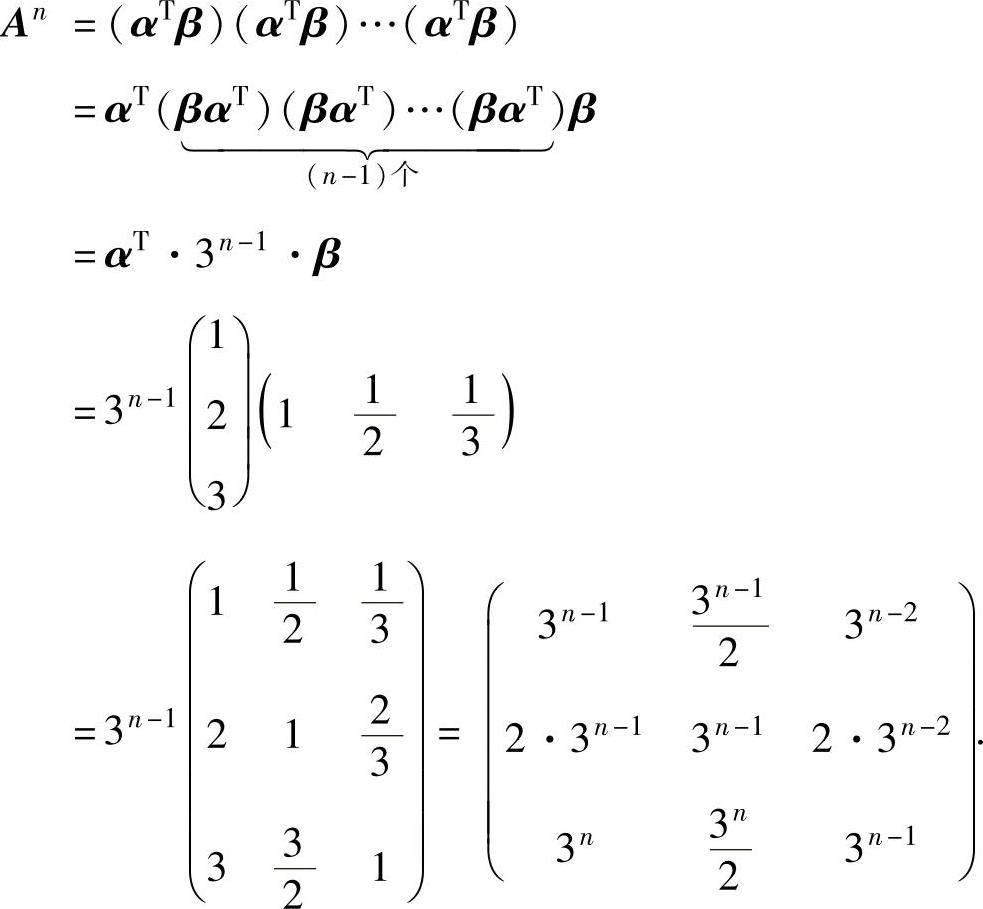
例5.3.2 已知n阶矩阵A，B只有第j列的对应元素不同，证明：

21-n|A+B|=|A|+|B|.

精解 由题意可设

978-7-111-46245-3-Part02-38.jpg

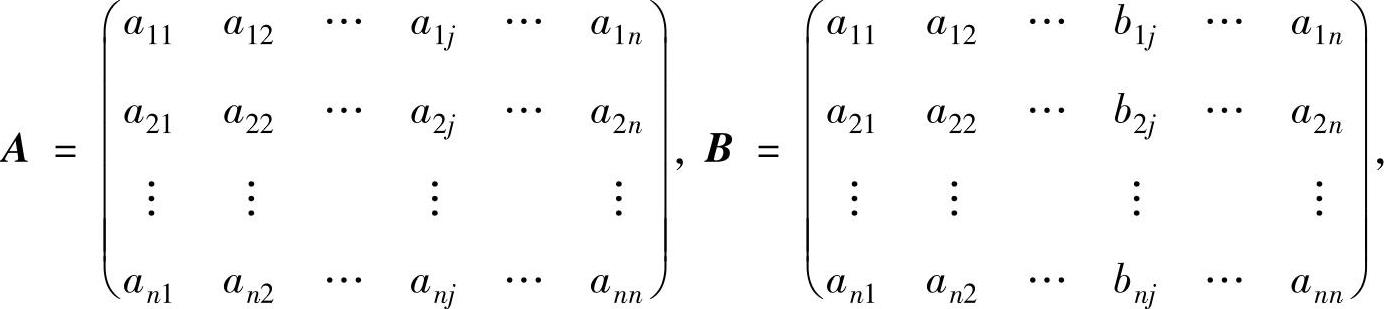
则

978-7-111-46245-3-Part02-39.jpg

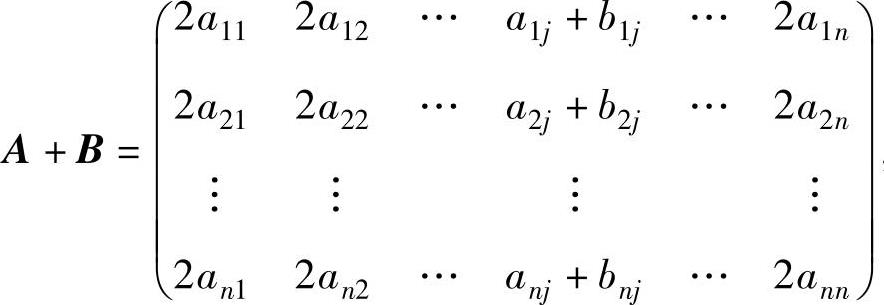
，所以

978-7-111-46245-3-Part02-40.jpg

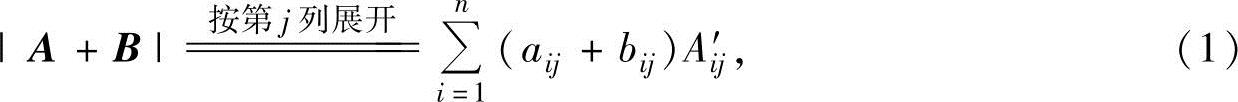
其中，Aij′是|A+B|的第i行第j列元素的代数余子式，显然，它是|A|的元素aij的代数余子式Aij的2n-1倍，也是|B|的元素bij的代数余子式Bij的2n-1倍，i=1，2，…，n.于是

978-7-111-46245-3-Part02-41.jpg

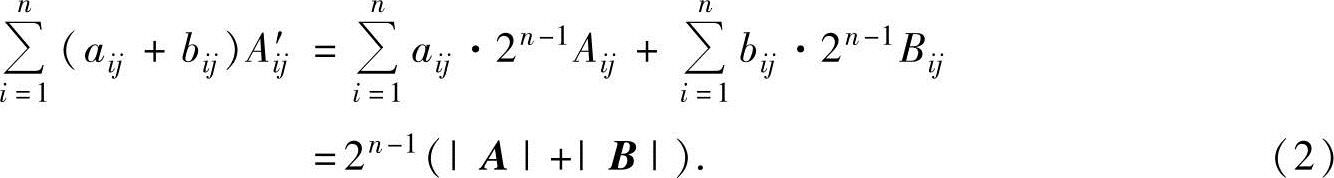
将式（2）代入式（1）得

|A+B|=2n-1（|A|+|B|），即21-n|A+B|=|A|+|B|.

例5.3.3 设n阶矩阵A，B，C满足AB=BC=CA=En，求A2+B2+C2.

精解 由AB=BC=CA=En得

A2=AEnA=A（BC）A=（AB）（CA）=E2n=En，

B2=BEnB=B（CA）B=（BC）（AB）=E2n=En，

C2=CEnC=C（AB）C=（CA）（BC）=E2n=En，

所以，A2+B2+C2=En+En+En=3En.

例5.3.4 设n阶矩阵A，B满足ATA=AAT=En，BTB=BBT=En，且|A|=-|B|，证明：|A+B|=0.

精解 由题设知，

|A+B|=|EnA+BEn|=|BBTA+BATA|

=|B||BT+AT||A|

=-|A|2|（A+B）T|=-|A|2|A+B|，即（1+|A|2）|A+B|=0.

由此推出|A+B|=0（因为1+|A|2>0）.