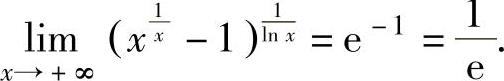十六、洛必达法则
【主要内容】
1.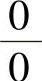 型未定式极限的洛必达法则
型未定式极限的洛必达法则
设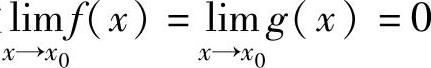 ,则称
,则称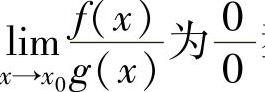 型未定式极限,这里的x0可以换成x0-,
型未定式极限,这里的x0可以换成x0-,
x0+,∞,-∞及+∞.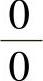 型未定式极限的洛必达法则(以x→x0情形为例)是:
型未定式极限的洛必达法则(以x→x0情形为例)是:
设函数f(x),g(x)在点x0的某个去心邻域内可导,且g′(x)≠0.如果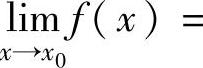
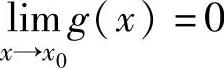 ,且
,且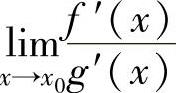 存在或为无穷大,则
存在或为无穷大,则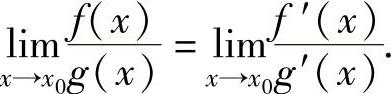
注 (ⅰ)对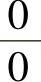 型未定式极限
型未定式极限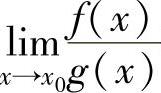 在使用洛必达法则之前应尽量进行化简,如利用极
在使用洛必达法则之前应尽量进行化简,如利用极
限运算法则算出其中非未定式部分的极限,对f(x)或g(x)作等价无穷小代替等.
(ⅱ)如果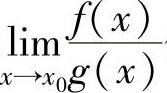 化简后仍是
化简后仍是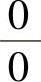 型未定式极限,记为
型未定式极限,记为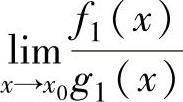 ,则可考虑应用洛必达
,则可考虑应用洛必达
法则.但是当f1(x)或g1(x)不易求导,或表达式比较复杂时,可将f1(x)或g1(x)按(x-x0)的幂展开成带佩亚诺型余项的泰勒公式,寻找f1(x)或g1(x)的在x→x0时的等价无穷
小,然后用等价无穷小代替算出 ,即
,即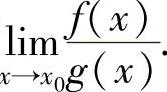
2. 型未定式极限的洛必达法则
型未定式极限的洛必达法则
设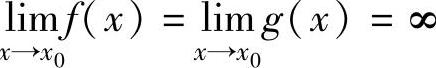 ,则称
,则称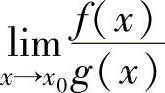 为
为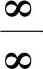 型未定式极限.这里的x→x0可以换成x0-,x0+,∞,-∞及+∞.
型未定式极限.这里的x→x0可以换成x0-,x0+,∞,-∞及+∞. 型未定式极限的洛必达法则(以x→x0情形为例)是:
型未定式极限的洛必达法则(以x→x0情形为例)是:
设函数f(x),g(x)在点x0的某个去心邻域内可导,且g′(x)≠0.如果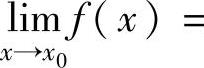
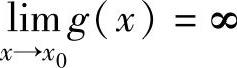 ,且
,且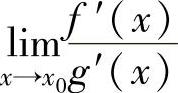 存在或为无穷大,则lim
存在或为无穷大,则lim
x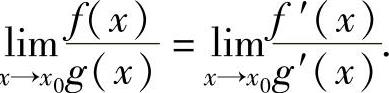
注 型未定式极限计算方法
型未定式极限计算方法
(ⅰ)应用 型洛必达法则计算;
型洛必达法则计算;
(ⅱ)用初等代数运算或变量代换将 型未定式极限转换成
型未定式极限转换成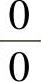 型未定式极限后再行计算.
型未定式极限后再行计算.
3.其他未定式极限计算方法
其他未定式还有∞-∞,0·∞,00,1∞,∞0等型(这里∞-∞表示:当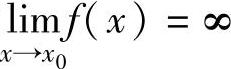 ,
,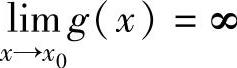 时的未定式极限
时的未定式极限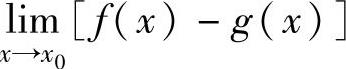 ,x0可以换成x0-,x0+,∞,-∞,+∞.
,x0可以换成x0-,x0+,∞,-∞,+∞.
至于0·∞,00,1∞,∞0型的未定式极限也可以同样理解).∞-∞与0·∞型未定式极限,可以先通过初等代数运算或变量代换转换成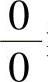 型或
型或 型
型
未定式极限,然后计算.00,1∞,∞0型未定式极限都是幂指函数的极限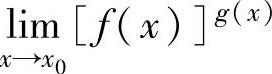 (这里以x→x0为例),
(这里以x→x0为例),
由于
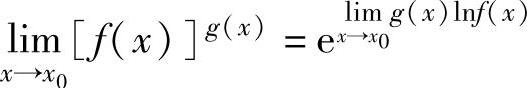 (https://www.daowen.com)
(https://www.daowen.com)
,
所以,只要算出0·∞型未定式极限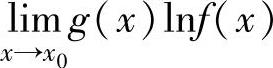 .如果它的值为A,则
.如果它的值为A,则
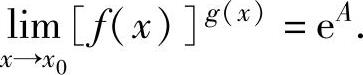
【典型例题】
例1.16.1 求极限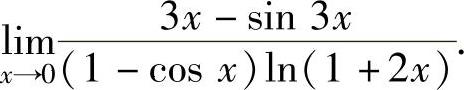
精解 所给极限是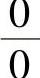 型未定式极限.
型未定式极限.
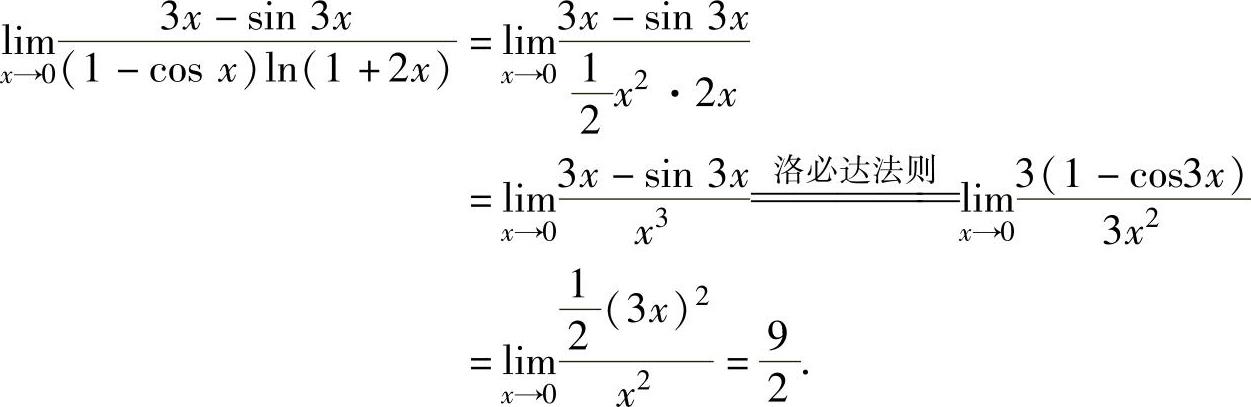
例1.16.2 求极限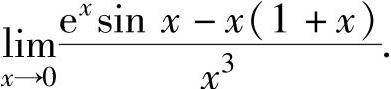
精解 所给极限是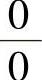 型未定式极限.
型未定式极限.

注 本题若用带佩亚诺型余项的麦克劳林公式算出exsinx-x(1+x)的等价无穷小,再利用等价无穷小代替定理计算更显快捷.
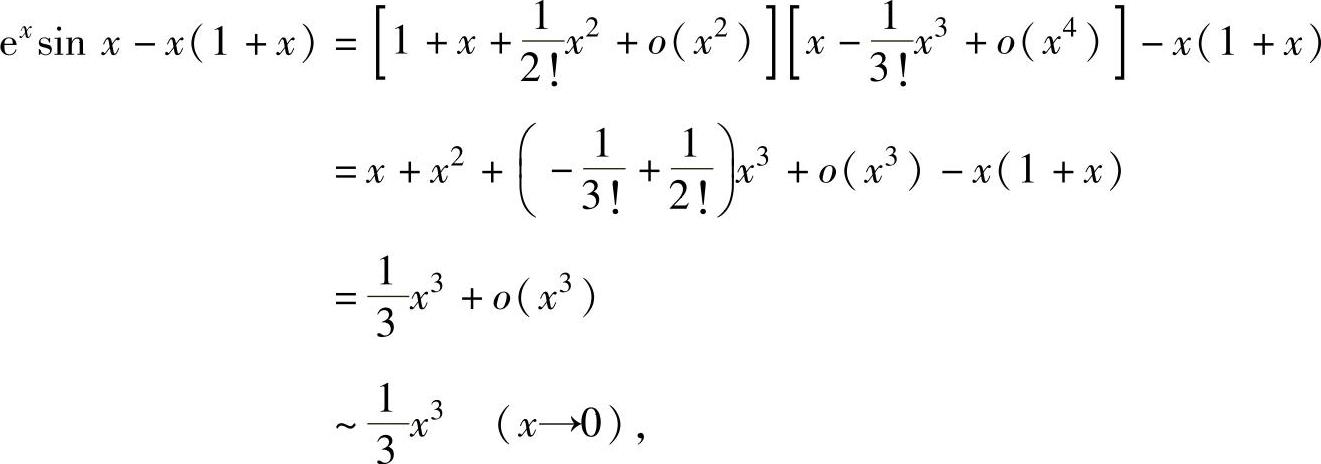
所以,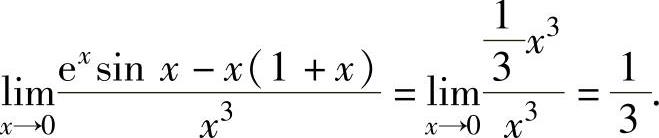
例1.16.3 求极限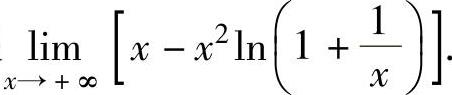
精解 所给极限是∞-∞型未定式极限.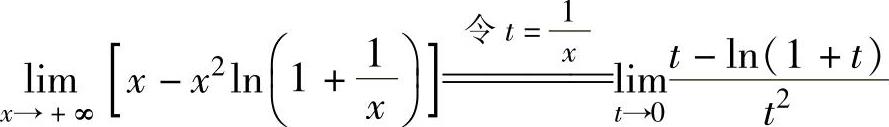 (00型未定式极限)
(00型未定式极限)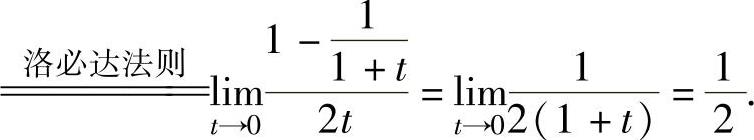
例1.16.4 求极限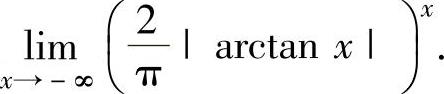
精解 所给极限是1∞型未定式极限.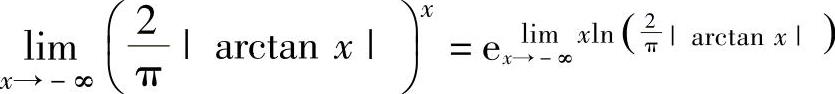 ,(1)
,(1)
其中,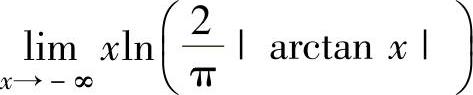 (0·∞型未定式极限)
(0·∞型未定式极限)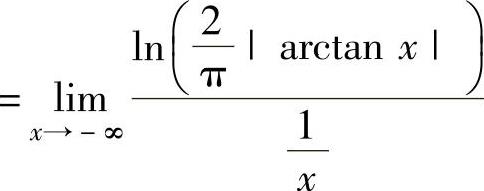 (00型未定式极限)
(00型未定式极限)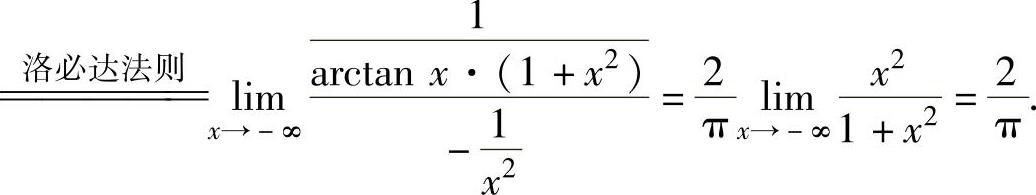
将它代入式(1)得

例1.16.5 求极限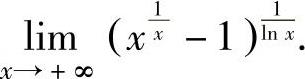
精解 由于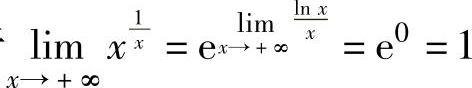 ,所以所给的极限是00型未定式极限.
,所以所给的极限是00型未定式极限.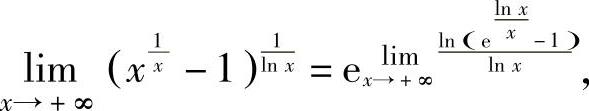 (1)
(1)
其中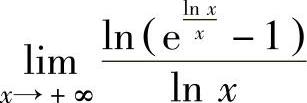 (∞∞型未定式极限)
(∞∞型未定式极限)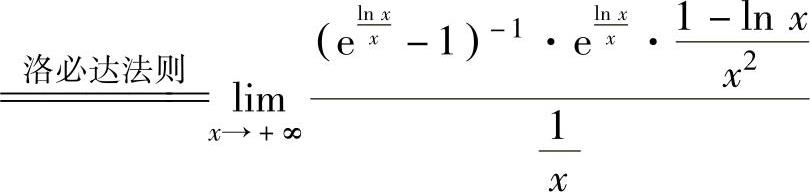
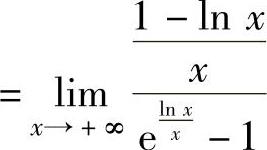 (00型未定式极限)
(00型未定式极限)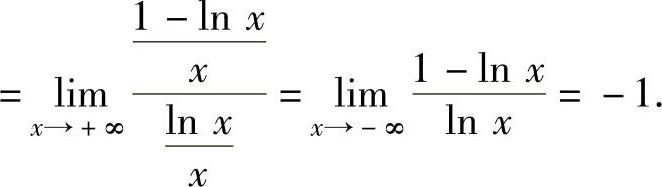
将它代入式(1)得