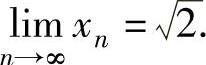数列极限存在准则
【主要内容】
数列极限可以用数列极限运算法则计算,也可将其看做函数极限用函数极限的计算方法来计算.但当用这些方法不易计算时,还可用数列极限存在准则计算数列极限.
数列极限存在准则有以下两条:
准则Ⅰ 设数列{xn},{yn}和{zn}.如果yn≤xn≤zn(n=1,2,…),且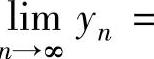
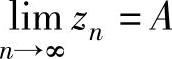 ,则
,则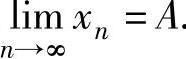
注 (ⅰ)对数列{xn}使用准则Ⅰ时,可通过适当缩小与放大xn,寻找数列{yn}和{zn}.(ⅱ)对函数也有类似准则Ⅰ的极限存在准则:设函数f(x),g(x),h(x).如果g(x)≤f(x)≤h(x)(在点x0的某个去心邻域内)且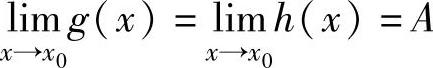 ,
,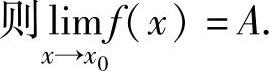
设函数f(x),g(x),h(x).如果g(x)≤f(x)≤h(x)(在|x|>N,N是某个正数),
且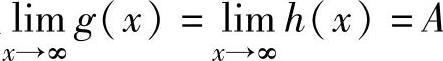 ,则
,则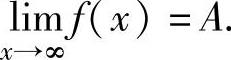
准则Ⅱ 如果数列{xn}单调不减(单调不增),且有上界(下界),则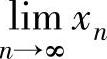 存在.
存在.
注 当数列{xn}是用递推式定义时,通常用极限存在准则Ⅱ计算这一数列的极限.一般来说,准则Ⅱ只能确定数列极限的存在,但在某些情况下,在确定其极限存在后还能算出这个极限值.
【典型例题】
例1.7.1 求数列极限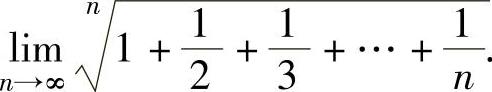
精解 记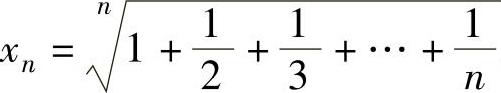 ,显然数列{xn}的极限不能用数列极限的运算法则
,显然数列{xn}的极限不能用数列极限的运算法则
计算,也不能转换成函数极限后用函数极限计算方法计算,因此考虑应用数列极限存在准则
Ⅰ计算.
由于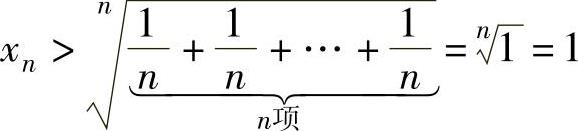 ,
,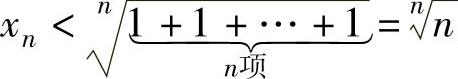 ,
,
并且nl→im∞1=nl→im∞nn=1,所以由数列极限存在准则Ⅰ得nlim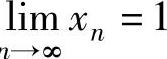 ,即
,即
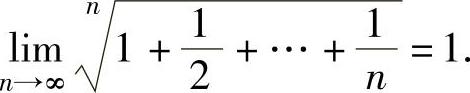
注 应记住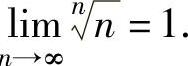
例1.7.2 设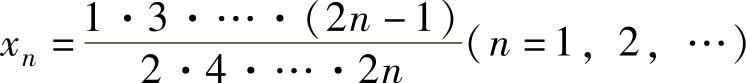 ,求极限
,求极限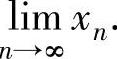
精解 用数列极限存在准则Ⅰ计算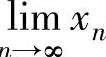 ,因此对xn作适当缩小与放大.
,因此对xn作适当缩小与放大.
由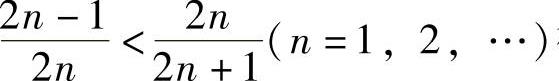 得
得
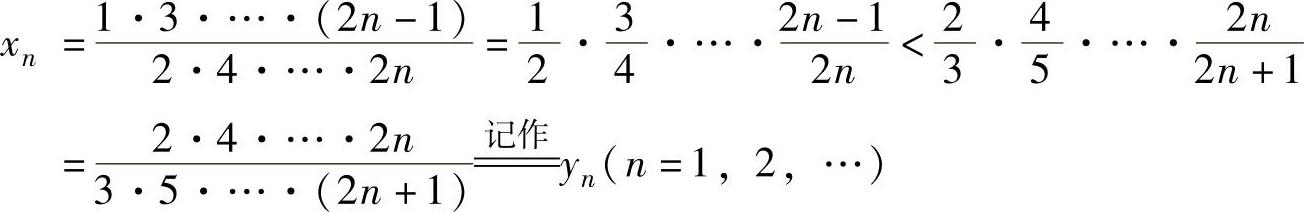
所以,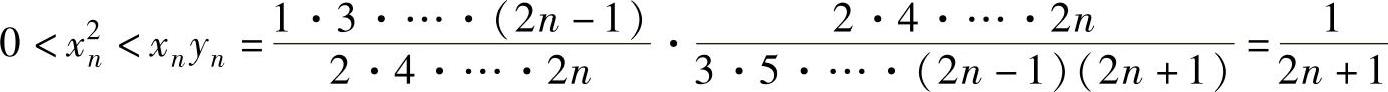 ,即
,即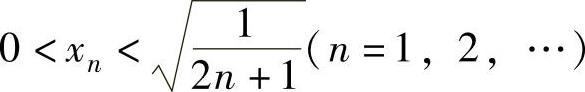 ,(https://www.daowen.com)
,(https://www.daowen.com)
且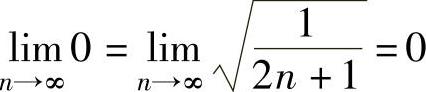 ,所以由数列极限存在准则Ⅰ得
,所以由数列极限存在准则Ⅰ得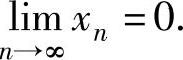
例1.7.3 设x1=10,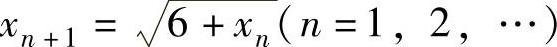 ,求极限limn→∞xn.
,求极限limn→∞xn.
精解 由于{xn}是由递推式定义的,所以用数列极限存在准则Ⅱ计算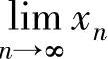
x1=10>3,x2=4>3,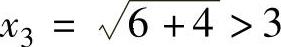 ,…依次类推可得xn>3 (n=1,2,…),即
,…依次类推可得xn>3 (n=1,2,…),即
{xn}有下界.
由于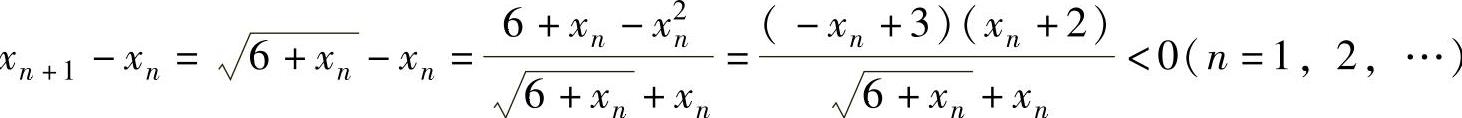 ,所
,所
以{xn}单调减少.从而由数列极限存在准则Ⅱ知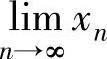 存在,记为A.
存在,记为A.
递推式两边令n→∞取极限得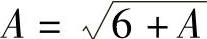 ,
,
此方程仅有解A=3.所以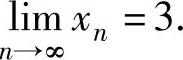
例1.7.4 设x1>0,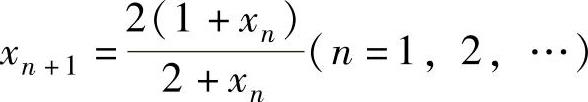 ,求极限
,求极限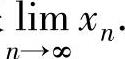
精解 由于{xn}是由递推式定义的,所以用数列极限存在准则Ⅱ计算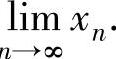
显然,xn>0(n=1,2,…),并且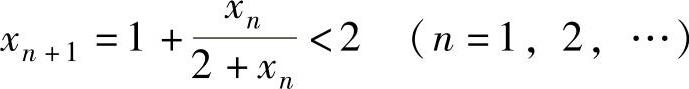 ,
,
所以,{xn}既有下界又有上界.
下面考虑{xn}的单调性.由于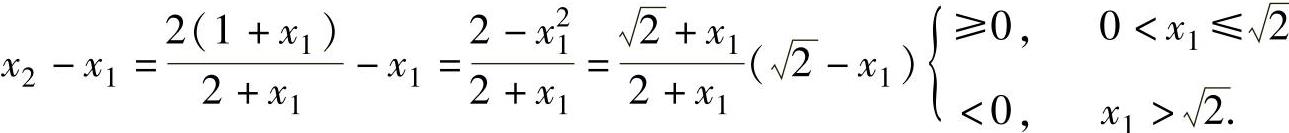 ,
,
当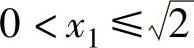 时,
时,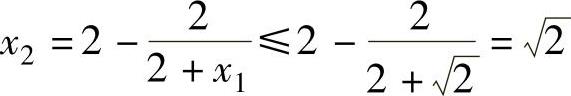 ,同理可证
,同理可证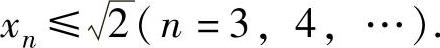 由
由
此可以推出,对n=1,2,…有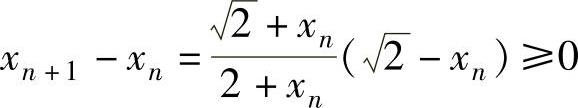 ,从而此时,{xn}单调不减;
,从而此时,{xn}单调不减;
当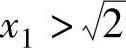 时,
时,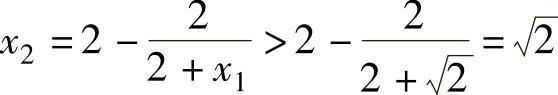 ,同理可证
,同理可证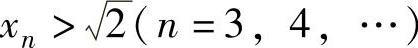 .由此可
.由此可
以推出,对n=1,2,…有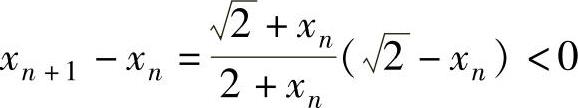 ,从而此时,{xn}单调减少.
,从而此时,{xn}单调减少.
由以上分析可知,{xn}按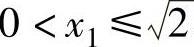 和
和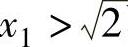 可为单调不减有上界的数列或单调减少有
可为单调不减有上界的数列或单调减少有
下界的数列,因此由数列极限存在准则Ⅱ知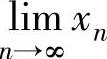 存在,记为A.
存在,记为A.
递推式两边令n→∞取极限得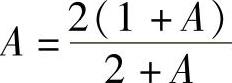 , 即
, 即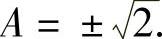
由于xn>0(n=1,2,…),所以A≥0,从而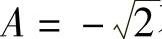 不合题意,舍去,由此得到
不合题意,舍去,由此得到