函数连续的定义

四 、函数连续的定义

【主要内容】

1.函数在点x₀处连续的概念

设函数f（x）在点x₀的某个邻域内有定义，如果，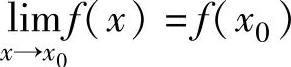

则称f（x）在点x₀处连续.

函数f（x）在点x₀处连续的充分必要条件是f（x）在点x₀既左连续（即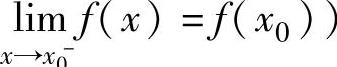

又右连续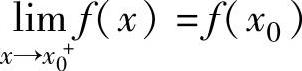（即），即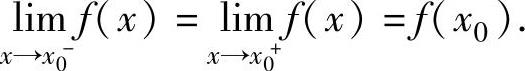

2.函数在开区间（a，b）内和闭区间[a，b]上连续的定义

如果函数f（x）在（a，b）的每一点处都连续，则称f（x）在（a，b）内连续.

如果函数f（x）在（a，b）内连续，且在点x=a处右连续，在点x=b处左连续，则称f（x）在[a，b]上连续.

注 初等函数在其定义域区间内或定义域区间上连续.

【典型例题】

例1.4.1 设函数f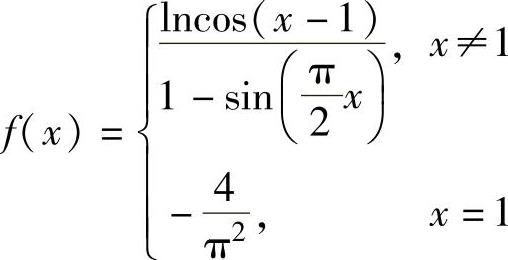，问f（x）在点x=1处是否连续？，

精解 按定义只要检验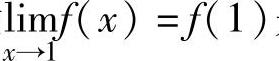是否成立即可.

由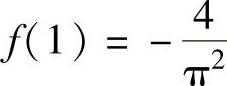，(https://www.daowen.com)

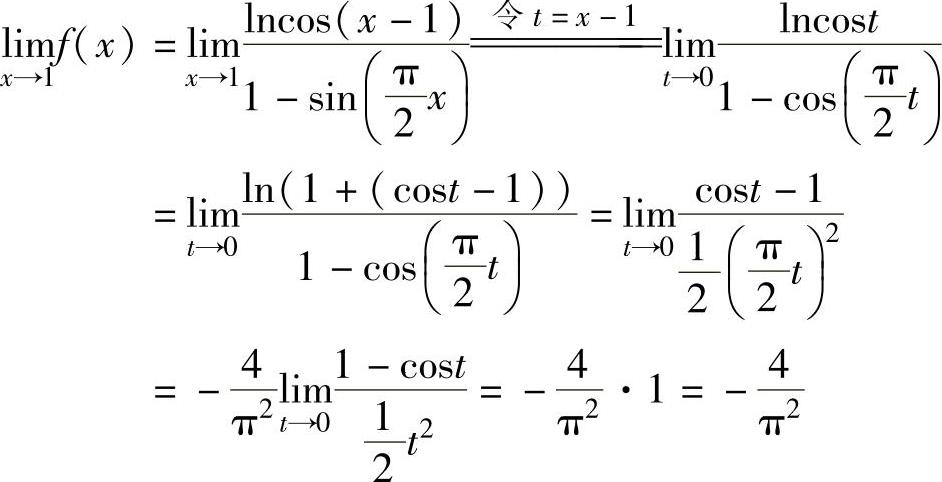
知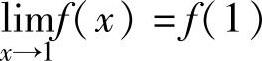，所以f（x）在点x=1处连续.

例1.4.2 设函数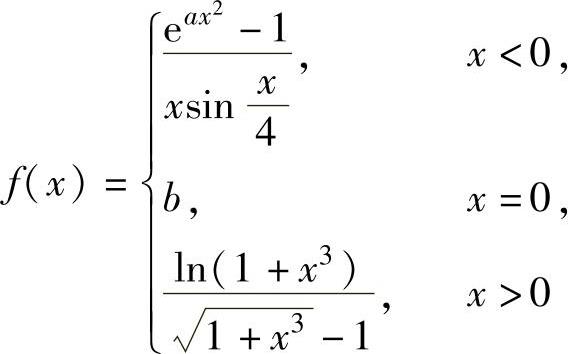在点x=0处连续，求常数a，b.

精解 根据f（x）在点x=0处连续的充分必要条件有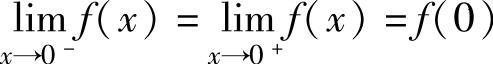，（1）

其中，，，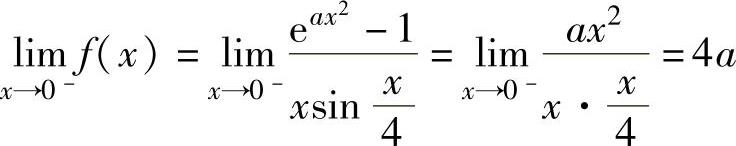

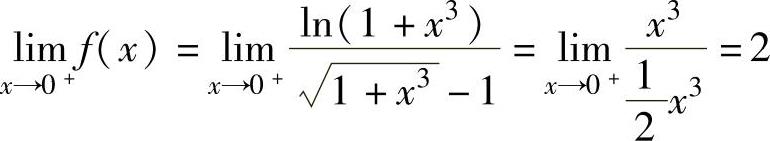f（0）=b.

将它们代入式（1）得4a=2=b，即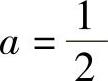，b=2.

例1.4.3 设函数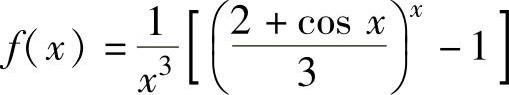，那么如何定义f（0）的值，使得f（x）在点x=0处连续.

精解 由函数在点x=0处连续的定义知，只要

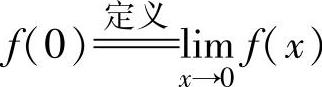
即可.由于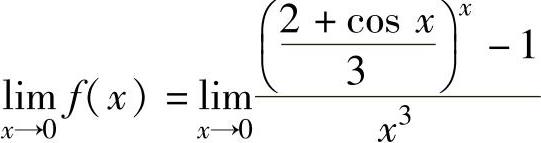，（1）

其中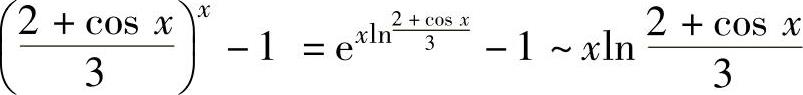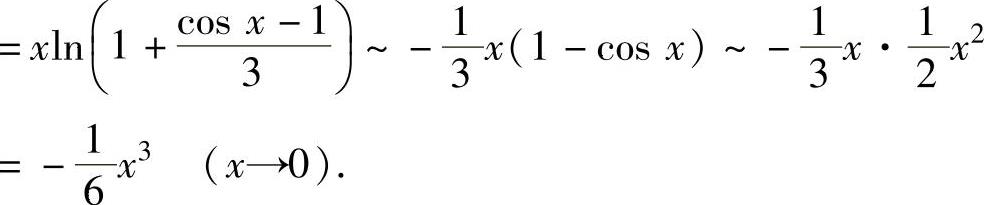，将它代入式（1）得

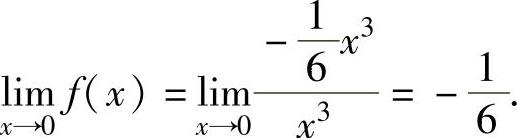
因此，定义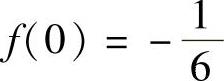，使得f（x）在点x=0处连续.