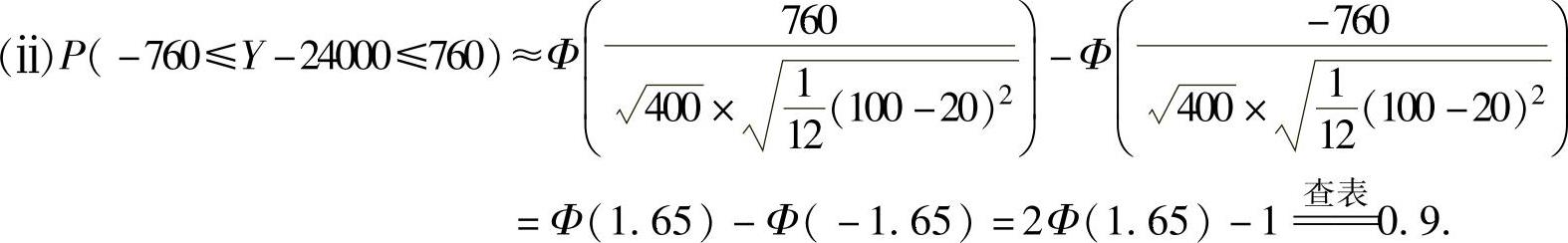练习题七解答
1.单项选择题
(1)B (2)B (3)D (4)B (5)B (6)C
(7)C (8)C (9)A (10)C (11)C (12)A
(13)B (14)D (15)D (16)B (17)D (18)D
(19)C (20)B (21)C (22)B (23)B (24)C
(25)B (26)C (27)C (28)C (29)B
2.解答题
(1)记Ai={甲机第i次开火击落乙机}(i=1,2),B={乙机开火击落甲机},则所求概率为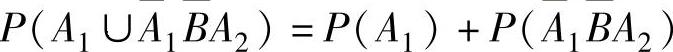
=P(A1)+P(A1)P(BA1)P(A2A1B)
=0.2+0.8×0.7×0.4=0.424.
(2)记A={取出的硬币是正品},B={投掷取出的硬币3次,每次都出现国徽},则所求概率为
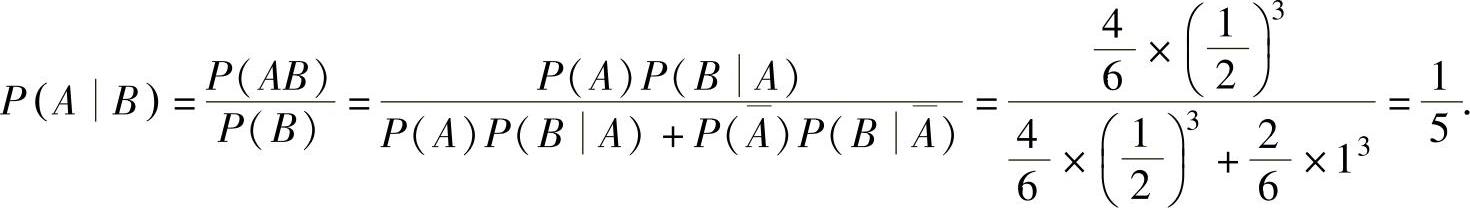
(3)记A1,A2,A3分别表示任取的是装有2个球、4个球和10个球的罐子,B={任取的球为红球}.
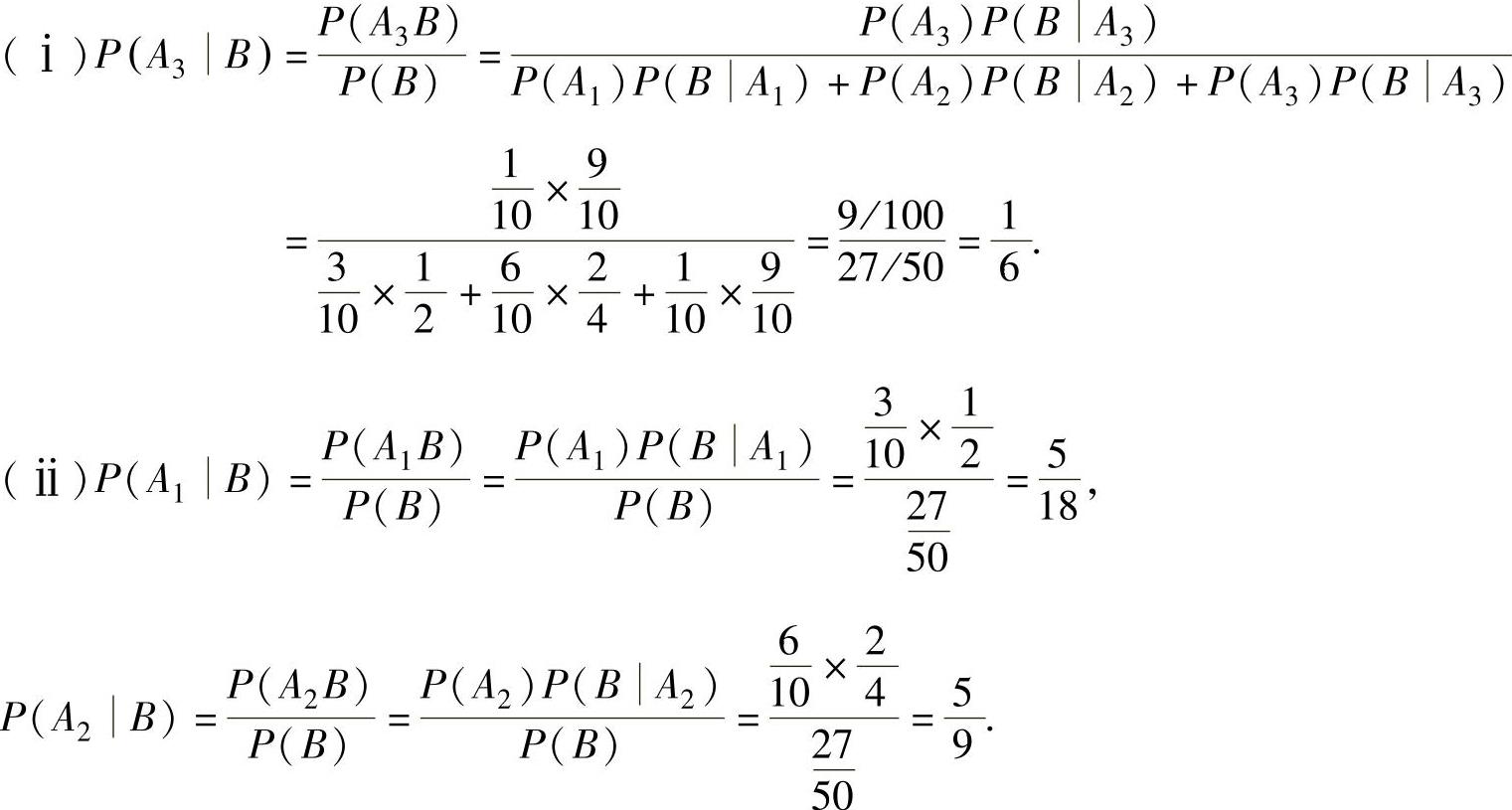
所以,所取的球最大可能来自装有4个球的罐子.
(4)由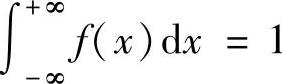 得
得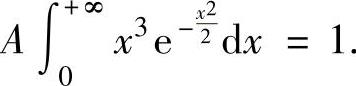 由于
由于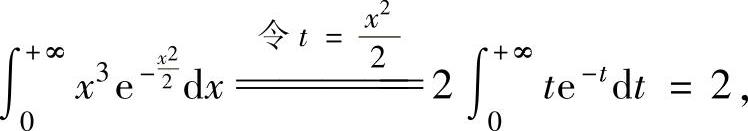
所以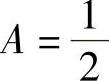 ,从而
,从而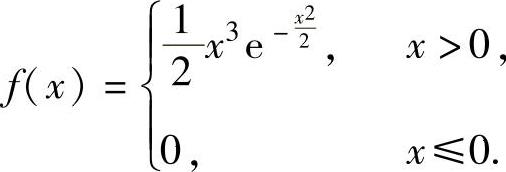 由此得到
由此得到
当x≤0时,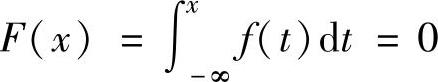 ;
;
当x>0时,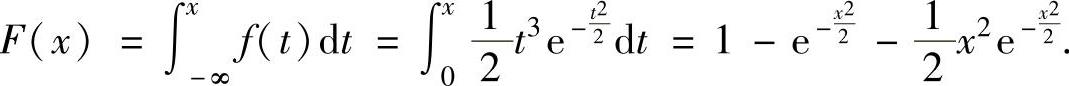
(5)p=P(X2-4Y≥0),而满足X2-4Y≥0的共有19种情形,所以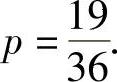 q=P(X2-4Y=0),而满足X2-4Y=0的共有2种情形,所以
q=P(X2-4Y=0),而满足X2-4Y=0的共有2种情形,所以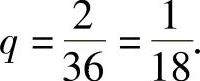
(6)Y可能取的值为0,2,且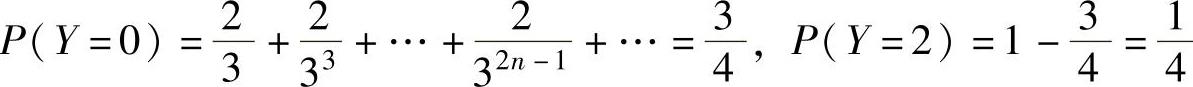 ,
,
Y的分布函数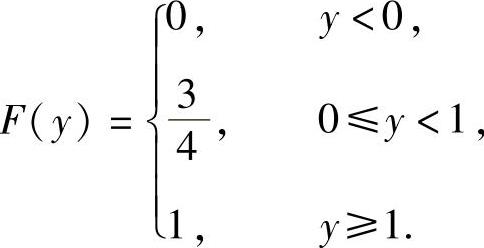
(7)记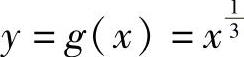 ,它在fX(x)≠0的区间(0,+∞)上单调、可导,且值域为(0,+∞),反函数x=h(y)=y3,所以
,它在fX(x)≠0的区间(0,+∞)上单调、可导,且值域为(0,+∞),反函数x=h(y)=y3,所以
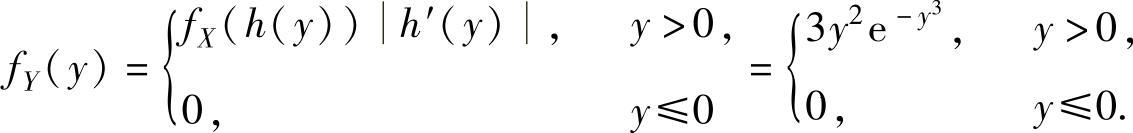
(8)当y<0时,P(Y≤y)=P(X2≤y)=P(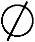 )=0.当0≤y<1时,P(Y≤y)=P(X2≤y)=P(-y≤X≤y)=F(y)-F(-y)=y.当y≥1时,P(Y≤y)=P(X2≤y)=P(-1≤X≤1)=F(1)-F(-1)=1,所以,
)=0.当0≤y<1时,P(Y≤y)=P(X2≤y)=P(-y≤X≤y)=F(y)-F(-y)=y.当y≥1时,P(Y≤y)=P(X2≤y)=P(-1≤X≤1)=F(1)-F(-1)=1,所以,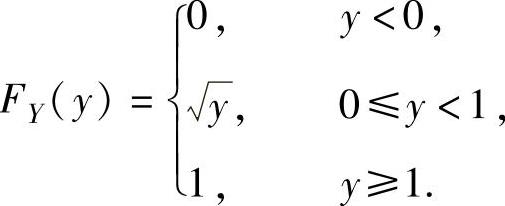
(9)X的分布函数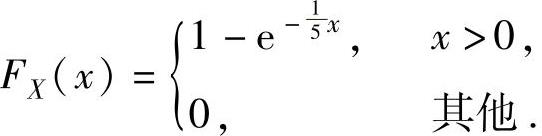 由题设知Y=min{X,2},所以,
由题设知Y=min{X,2},所以,
P(Y≤y)=P(min{X,2}≤y)=1-P(min{X,2}>y)=1-P(X>y,2>y).其中,当y≥2时,P(X>y,2>y)=0,
当y<2时,P(X>y,2>y)=P(X>y)=1-FX(y).所以,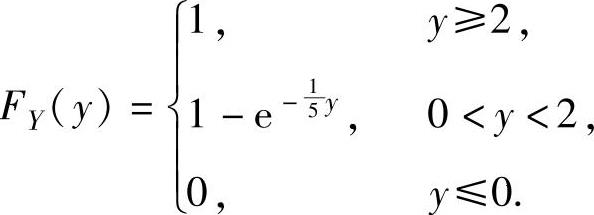
(10)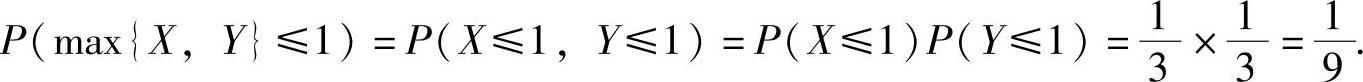
(11)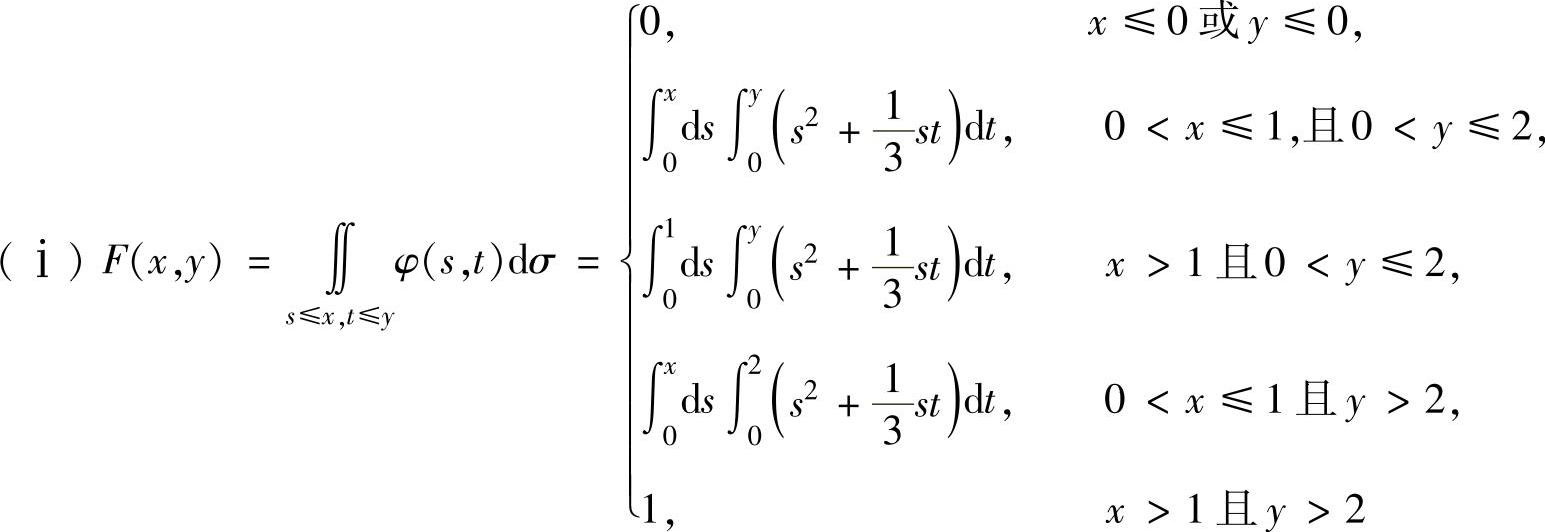
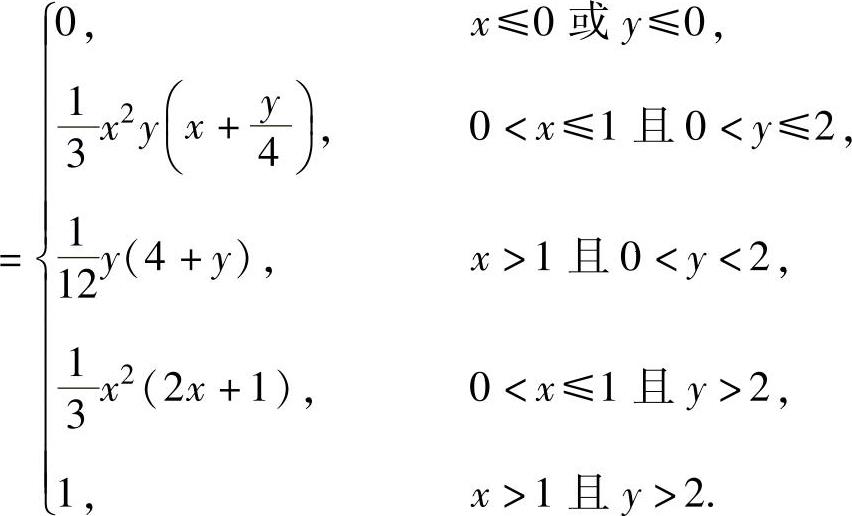
(ⅱ)关于Y的边缘概率密度
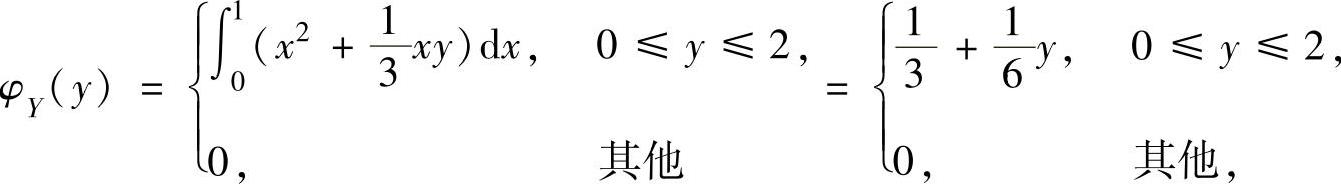
所以,对y∈[0,2],在Y=y的条件下,X的条件概率密度
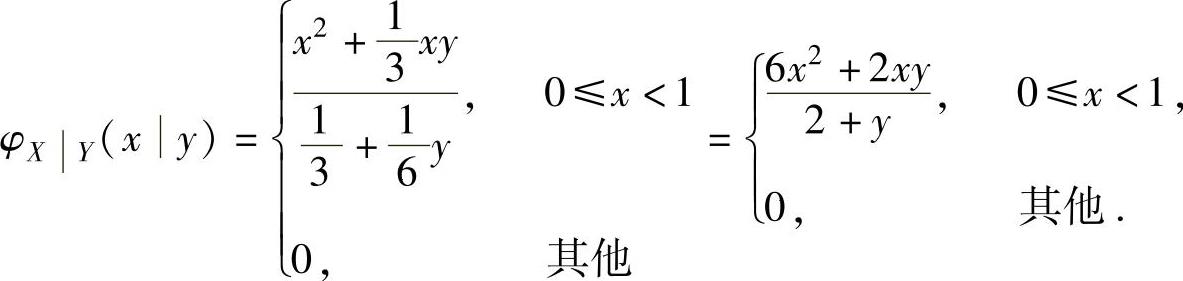
(12)由(X,Y)的概率密度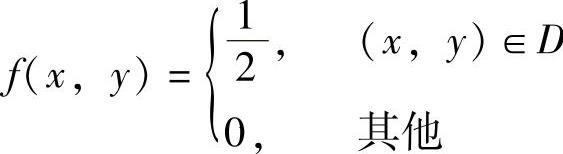 ,得关于X的边缘概率密度
,得关于X的边缘概率密度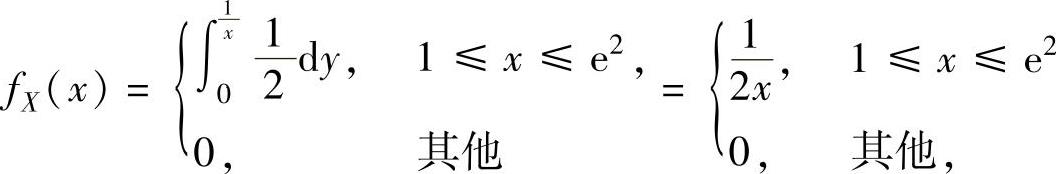 ,所以
,所以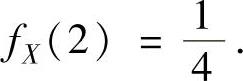
从而,
(13)由题设知,(X,Y)的分布律为
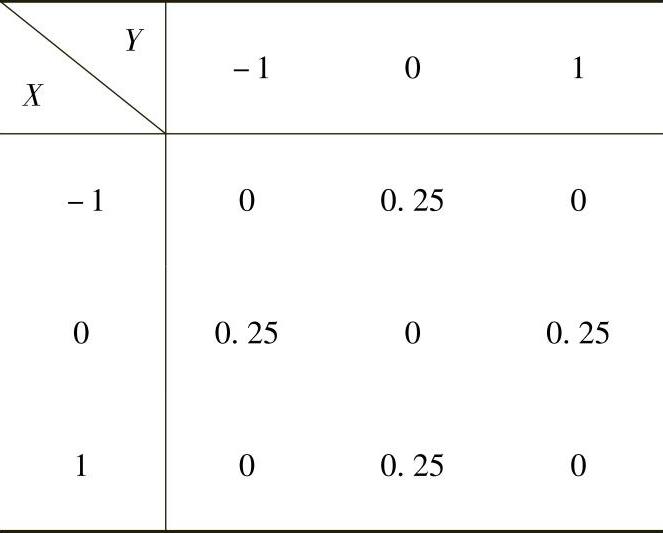
所以 P(X2=Y2)=P(X=-1,Y=-1)+P(X=-1,Y=1)+P(X=1,Y=-1)+
P(X=1,Y=1)+P(X=Y=0)=0,
P(Y<X2)=P(X=-1,Y=-1)+P(X=0,Y=-1)+P(X=1,Y=-1)+
P(X=-1,Y=0)+P(X=1,Y=0)=0.75.
(14)X可能取的值为0,1,2,…,Y可能取的值也为0,1,2,…且P(X=m,Y=n)=P(X=m)P(Y=nX=m)=(1-p)mp·(1-p)np=p2(1-p)m+n,m,n=0,1,2…故X与Y相互独立.
(15)(ⅰ)X1的分布律为
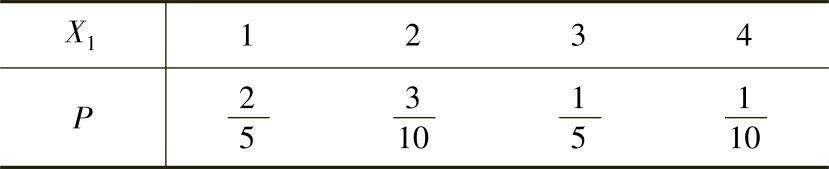
X2的分布律为
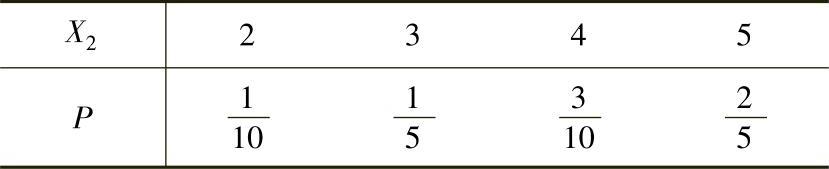
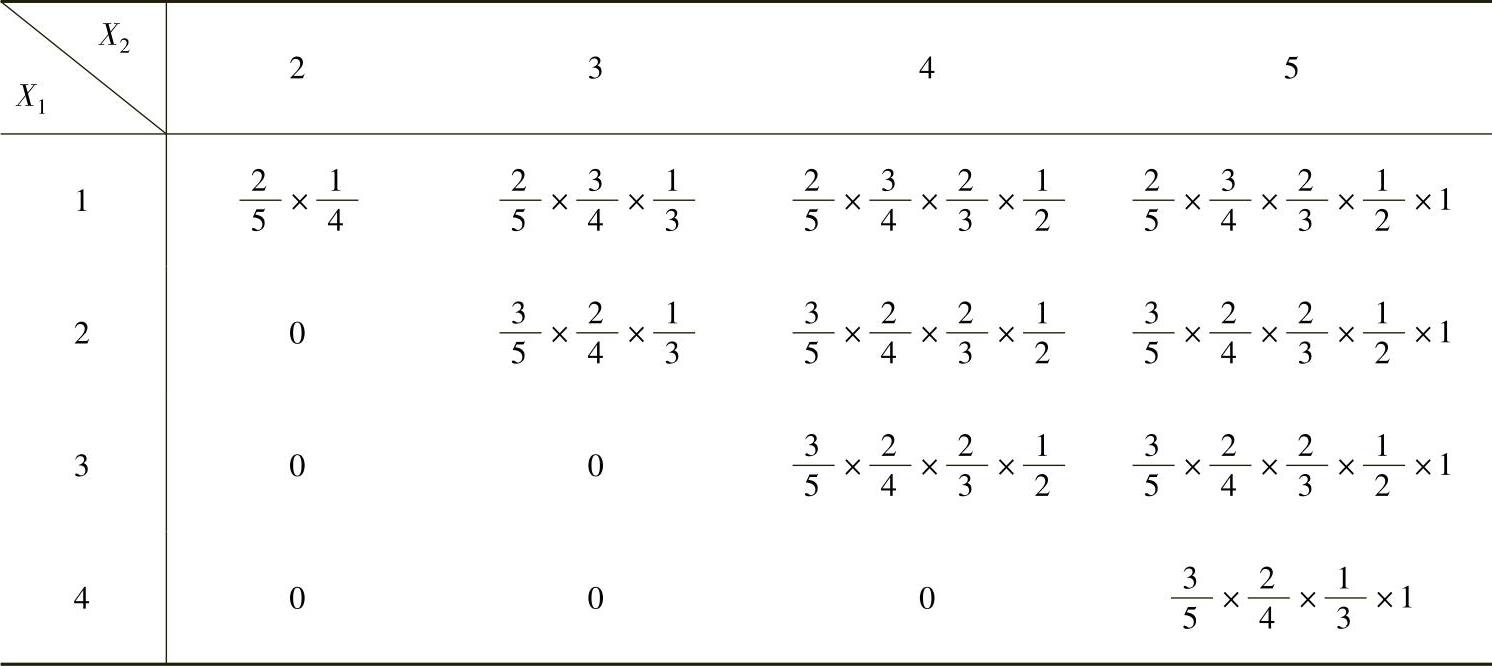
(ⅱ)(X1,X2)的分布律为即(https://www.daowen.com)
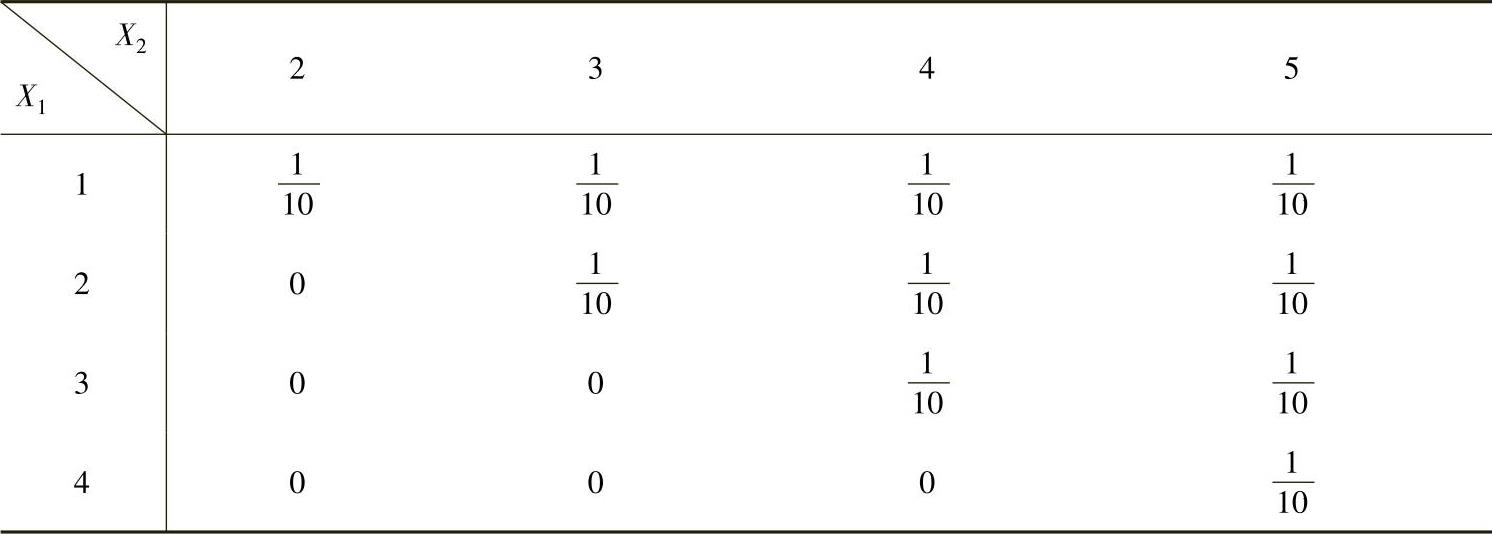
(16)(ⅰ)Y的分布函数
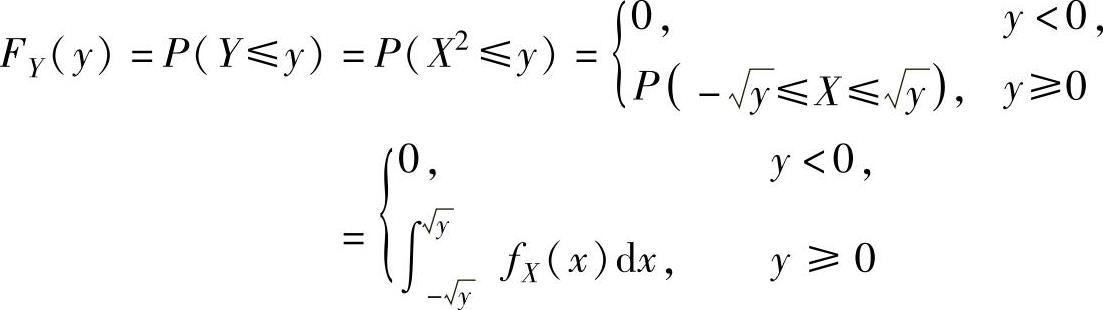
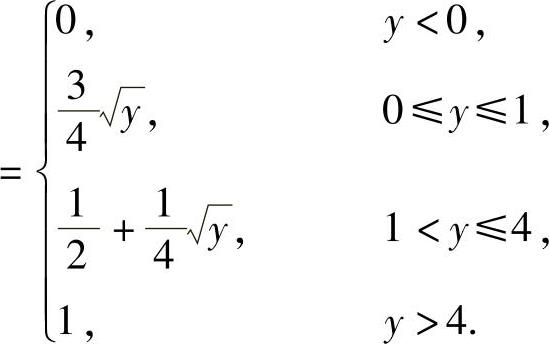
(ⅱ)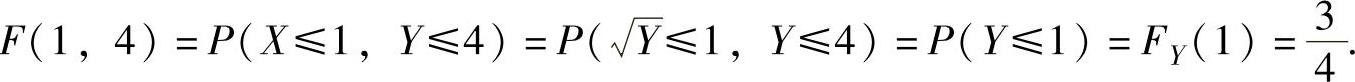
(17)(ⅰ)记D={(x,y)0<x<1,0<y<1},D1={(x,y)x≥2y},则D∩D1如图答7.2.19阴影部分所示.
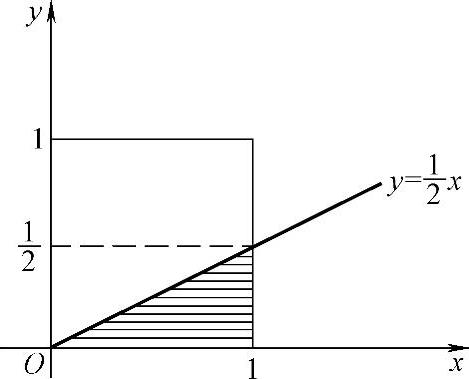
图 答7.2.19
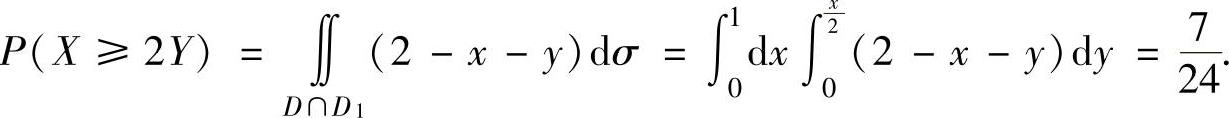
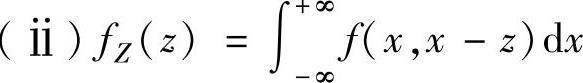 ,
,
其中,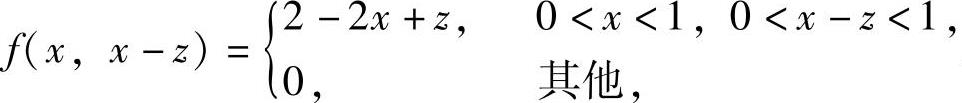 所以
所以
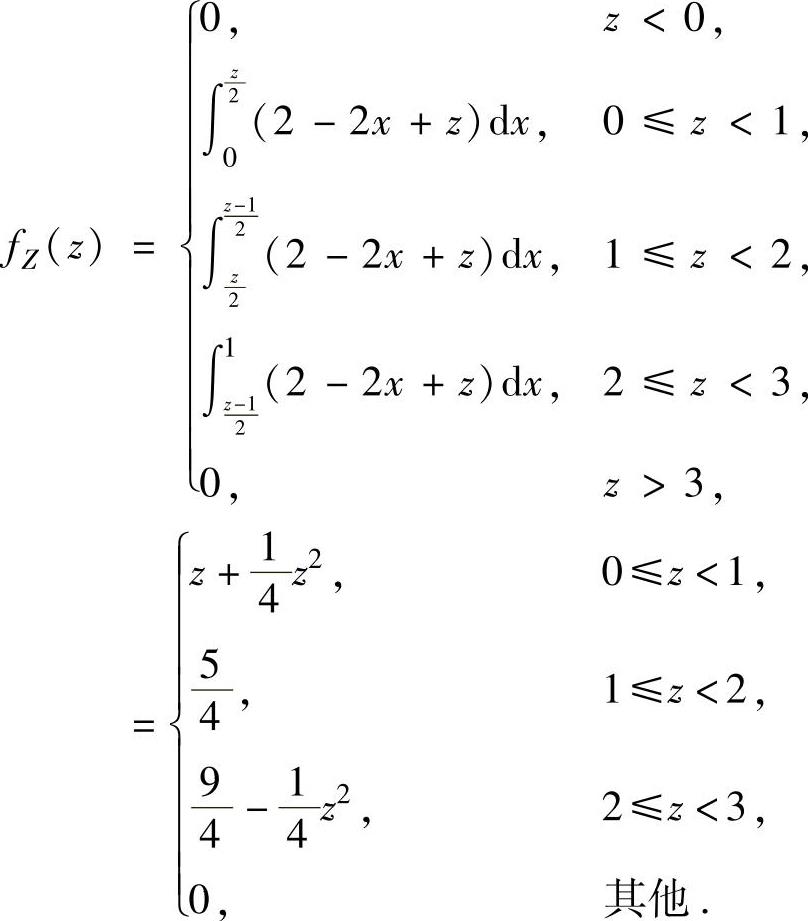
(18)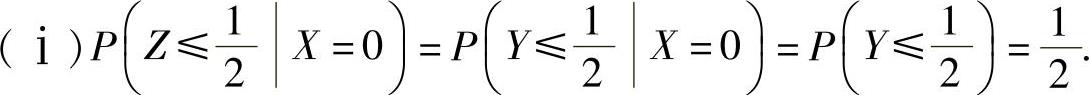
(ⅱ)Z的分布函数为
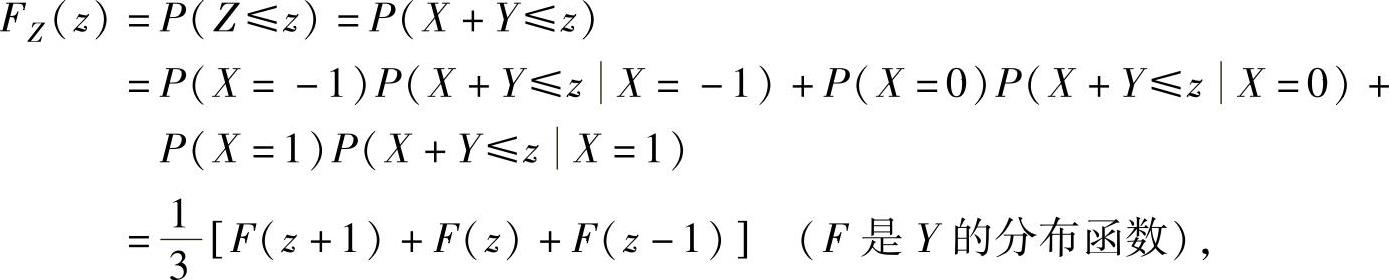
所以,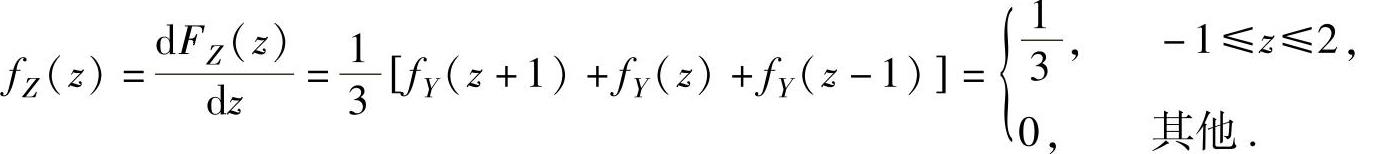
(19)由题设知,X,Y相互独立,且关于它们的边缘概率密度分别为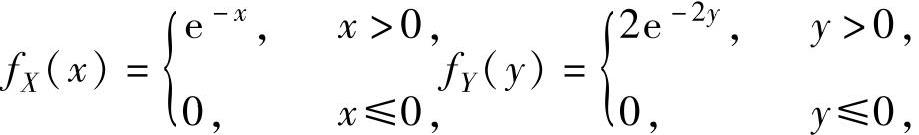
所以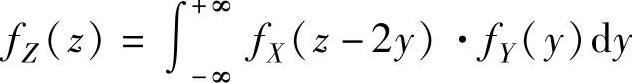 ,
,
其中,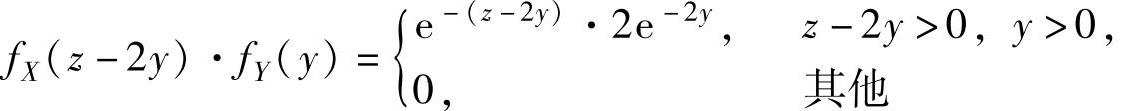
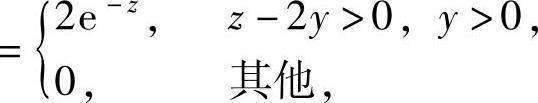
所以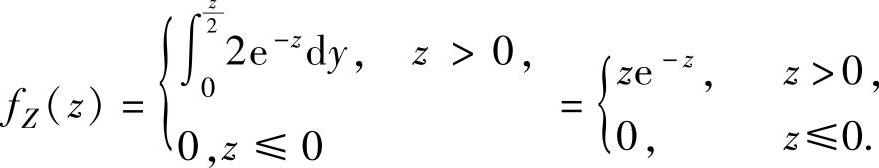
(20)a,b,c应满足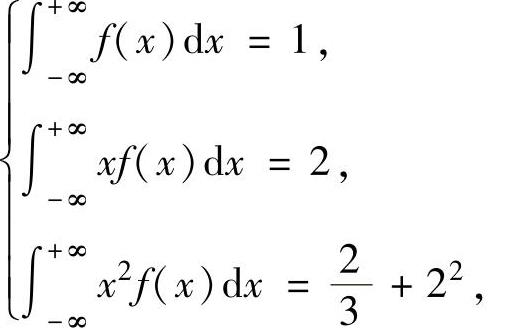 即
即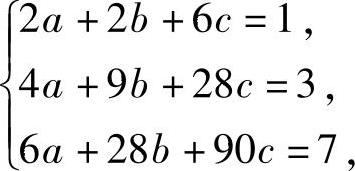
所以,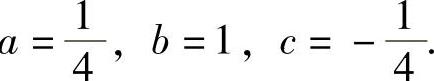 于是
于是
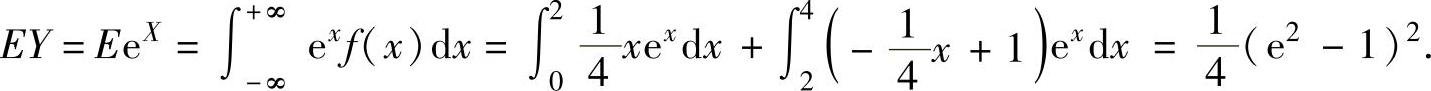
(21)由于(X,Y)的概率密度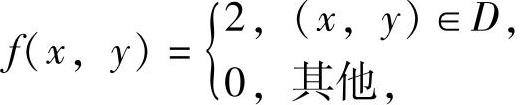
所以,关于X和关于Y的边缘概率密度分别为
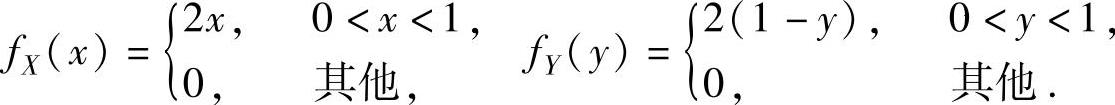
由此得到,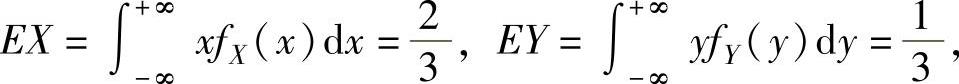
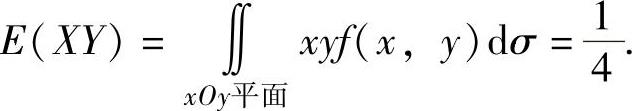
因此,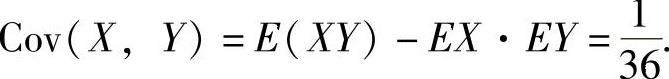
(22)由于DU=4DX+DY=5λ>0,DV=4DX+9DY=13λ>0,
Cov(U,V)=4DX-4E(XY)-3DY=4λ-4EX·EY-3λ=λ-4λ2,所以,U与V的相关系数为
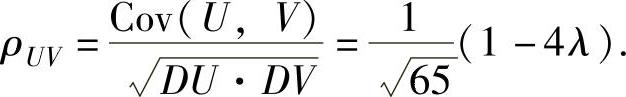
(23)X的概率密度为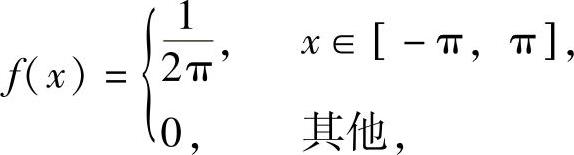 所以
所以
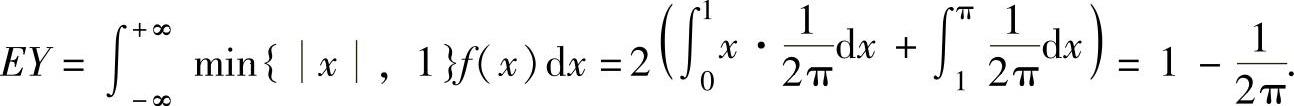
此外,由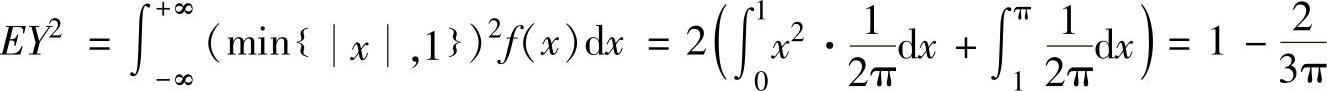
得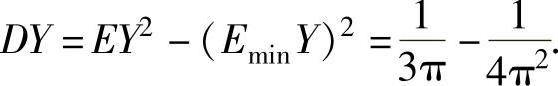
(24)由于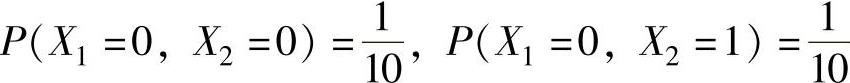 ,
,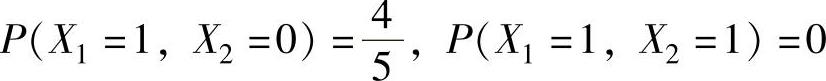 ,
,
所以(X1,X2)的分布律及边缘分布律为
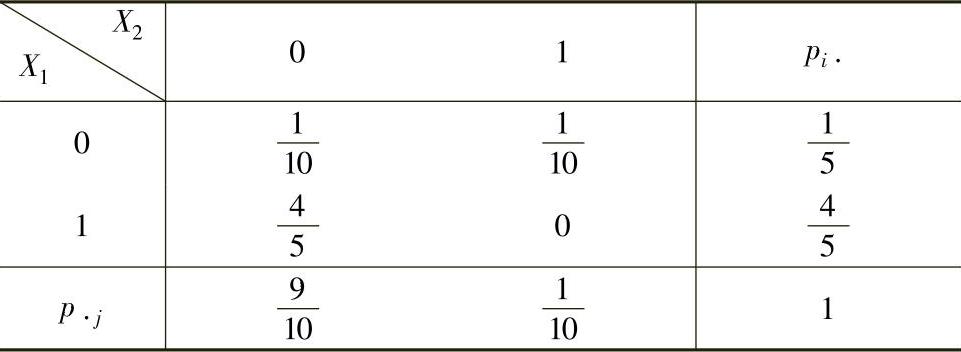
由此得到,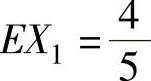 ,
,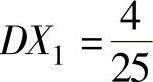 ;
;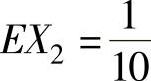 ,
,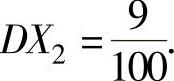
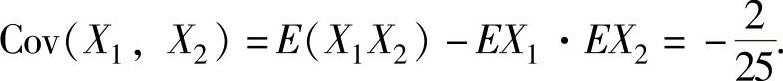
因此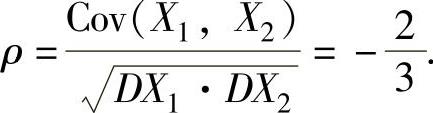
(25)(ⅰ)设第i位顾客的消费额为Xi(元),则Xi~U[20,100](i=1,2,…,400).记该餐厅
的日营业额为Y(元),则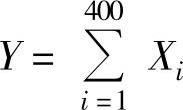 ,从而
,从而