方程不同实根个数的判定
【主要内容】
1.设函数f(x)在[a,b]上连续,且f(a)f(b)<0,则方程f(x)=0在(a,b)内有实根.这一结论有各种推广形式,例如,
(1)设函数f(x)在(a,b)内连续,且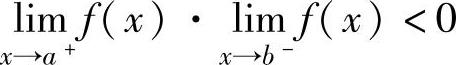 ,则方程f(x)=0在(a,
,则方程f(x)=0在(a,
b)内有实根.
(2)设函数f(x)在[a,+∞)上连续,且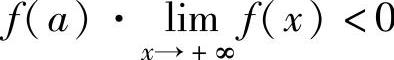 ,则方程f(x)=0在[a,
,则方程f(x)=0在[a,
+∞)上有实根.
2.设f(x)是[a,b]上的连续单调函数,且f(a)f(b)<0,则方程f(x)=0在(a,b)内有唯一实根.这一结论也可表示为如下形式:
设函数f(x)在[a,b]上连续,在(a,b)内可导且f′(x)>0(或f′(x)<0),此外,f(a)f(b)<0,则方程f(x)=0在(a,b)内有唯一实根.
以上结论有各种推广形式,例如,
(1)设函数f(x)在(a,b)内可导且f′(x)>0(或f′(x)<0),此外,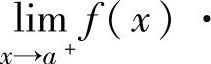
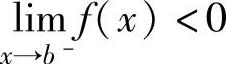 ,则方程f(x)在(a,b)内有唯一实根.
,则方程f(x)在(a,b)内有唯一实根.
(2)设函数f(x)在(a,+∞)上可导且f′(x)>0(或f′(x)<0),此外,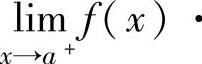
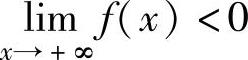 ,则方程f(x)在(a,+∞)上有唯一实根.
,则方程f(x)在(a,+∞)上有唯一实根.
【典型例题】
例1.21.1 设函数f(x)在[a,b]上可导,且f′(x)<1.又设对任意x∈[a,b],有a<f(x)<b,记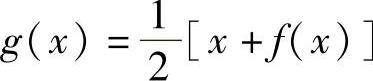 ,证明:方程g(x)=x在(a,b)内有唯一实根.
,证明:方程g(x)=x在(a,b)内有唯一实根.
精解 记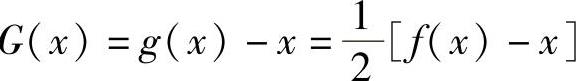 ,则G(x)在[a,b]上可导且
,则G(x)在[a,b]上可导且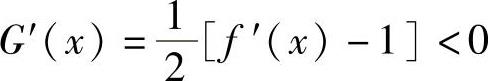 (利用题设f′(x)<1).
(利用题设f′(x)<1).
此外,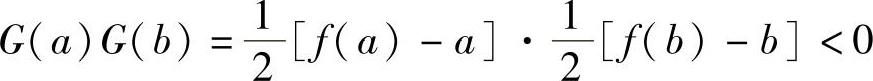 ,所以方程G(x)=0,即g(x)=x在
,所以方程G(x)=0,即g(x)=x在
(a,b)内有唯一实根.
例1.21.2 求方程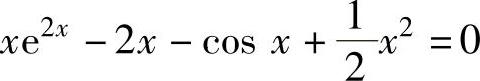 在(0,1)内的实根个数.
在(0,1)内的实根个数.
精解 记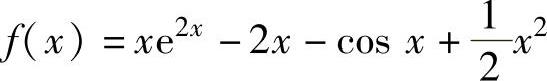 ,则f(x)在[0,1]上二阶可导且
,则f(x)在[0,1]上二阶可导且
f′(x)=(1+2x)e2x-2+sinx+x,
f″(x)=4(1+x)e2x+cosx+1>0,即f′(x)在(0,1)内单调增加,此外
f′(0)f′(1)=(-1)·(3e2-1+sin1)<0,所以,方程f′(x)=0在(0,1)内有唯一实根,记为x0,则有
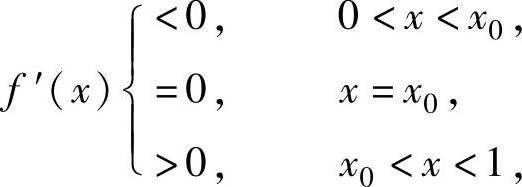
x0将(0,1)分成两个子区间(0,x0)和(x0,1).
当x∈(0,x0)时,f(x)<f(0)=-1<0,所以方程f(x)=0在(0,x0)内无实根.
当x∈(x0,1)时,由于f(x)是单调增加,且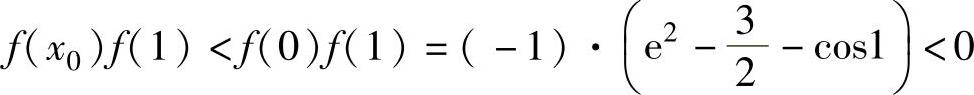 ,(https://www.daowen.com)
,(https://www.daowen.com)
所以,方程在(x0,1)内有唯一实根.
综上所述,方程在(0,1)内有唯一实根.
例1.21.3 讨论方程karctanx-x=0不同实根个数与参数k的关系.
精解 记f(x)=karctanx-x,显然不论k取何值,x=0都是方程f(x)=0的实根.
由于f(x)是奇函数,因此可从计算方程f(x)=0在(0,+∞)上的不同实根个数入手.
由于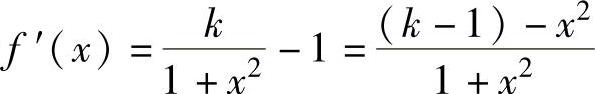 ,所以:
,所以:
当k-1≤0,即k≤1时,f′(x)<0,即f(x)在(0,+∞)上单调减少,于是
f(x)<f(0)=0 (x∈(0,+∞)),
由此可知,此时方程f(x)=0在(0,+∞)上无实根.
当k-1>0,即k>1时,
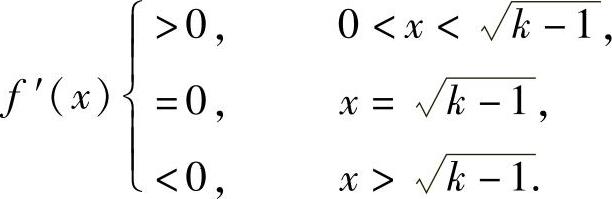
于是,对 ,f(x)>f(0)=0知,方程f(x)=0在
,f(x)>f(0)=0知,方程f(x)=0在 上无实根;对
上无实根;对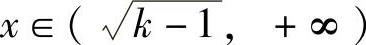 ,f′(x)<0,并且
,f′(x)<0,并且 ,
,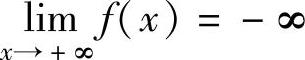 ,即
,即
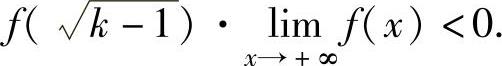
所以,此时方程f(x)=0在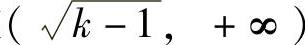 上有唯一实根,记为x0.
上有唯一实根,记为x0.
综上所述,当k≤1时,方程f(x)=0仅有实根x=0;当k>1时,方程f(x)=0有三个不同的实根:x=x0,x=0及x=-x0.
例1.21.4 讨论参数a的取值范围与方程2x3-9x2+12x-a=0的不同实根个数之间的关系.
精解 记f(x)=2x3-9x2+12x-a,按f(x)的驻点将其定义域划分成若干个小区间,然后在每个小区间上(注意:在每个小区间上f(x)都是单调的)考虑方程f(x)=0有无实根与a取值的关系即可.
由f′(x)=6(x2-3x+2)=6(x-1)(x-2)知f(x)的驻点为x=1,2.据此列表如下.

由表可知,
当5-a>0且4-a<0,即4<a<5时,方程f(x)=0在(-∞,1),(1,2)及(2,+∞)上都有唯一实根,即此时方程f(x)=0有三个不同实根.
当5-a=0,即a=5时,方程f(x)=0在(2,+∞)上有唯一实根,此外有实根x=1,即此时方程f(x)=0有两个不同实根.
当4-a=0,即a=4时,方程f(x)=0在(-∞,1)上有唯一实根,此外有实根x=2,即此时方程f(x)=0有两个不同实根.
当5-a<0,即a>5时,方程f(x)=0仅在(2,+∞)上有唯一实根,即此时方程f(x)=0只有一个实根.
当4-a>0,即a<4时,方程f(x)=0仅在(-∞,1)上有唯一实根,即此时方程f(x)=0只有一个实根.
