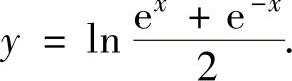可降阶的二阶微分方程

三 、可降阶的二阶微分方程

【主要内容】

二阶微分方程的一般形式是F（x，y，y′，y″）=0（其中y″必定出现），它的标准形是y″=f（x，y，y′）.

有三类二阶微分方程可降阶成一阶微分方程，然后求解，分别如下：

1.微分方程y″=f（x）.

求这类微分方程通解的步骤如下：

（1）降阶成一阶微分方程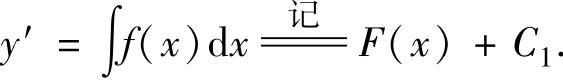

（2）于是二阶微分方程的通解为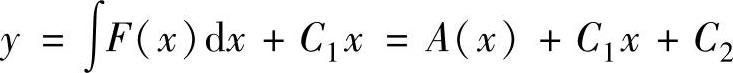（其中，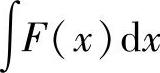

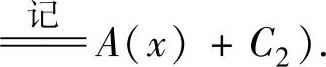
2.微分方程y″=f（x，y′）

求这类微分方程通解的步骤如下：

（1）令p=y′降阶为一阶微分方程p′=f（x，p），设它的通解为p=φ（x，C₁），即

（2）求解式（∗）得二阶微分方程的通解为

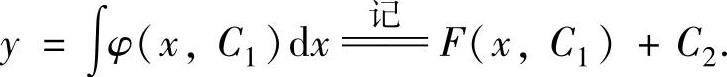
3.微分方程y″=f（y，y′）

求这类微分方程通解的步骤如下：

（1）令p=y′降阶成一阶微分方程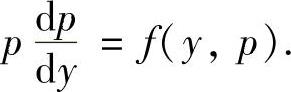设它的通解为p=φ（y，C₁），即

（2）求解式（∗∗）得二阶微分方程的通解

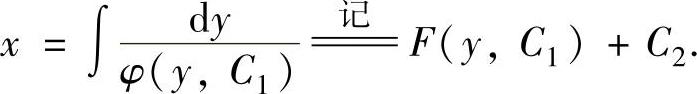
【典型例题】

例4.3.1 求微分方程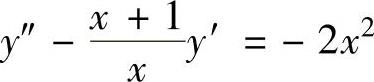的通解.

精解 所给微分方程是y″=f（x，y′）类型的二阶微分方程，所以令p=y′，则所给微分方程降阶为

式（1）的通解

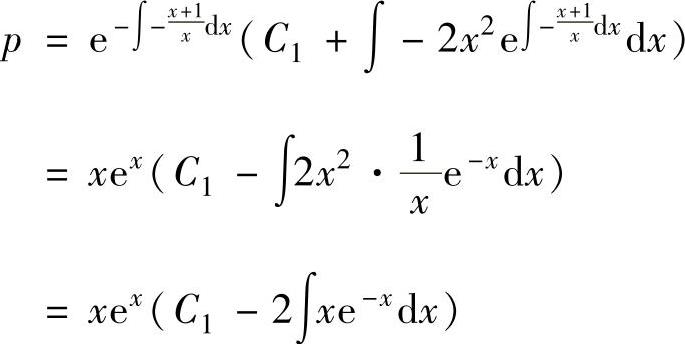
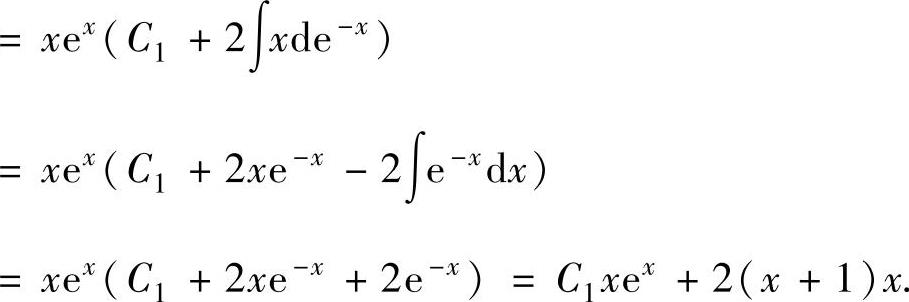
由此得到

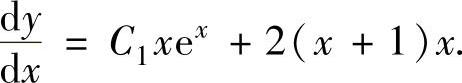
因此，原微分方程的通解为

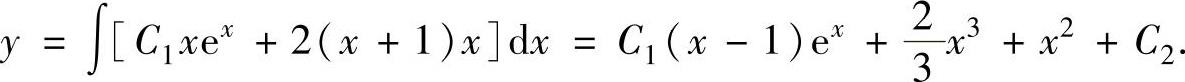
例4.3.2 求微分方程xy″+x（y′）2-y′=0满足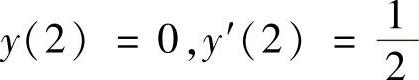的特解.(https://www.daowen.com)

精解 所给微分方程是y″=f（x，y′）类型的二阶微分方程，所以令p=y′，则所给微分方程降阶成，即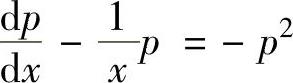（n=2的伯努利方程）.（1）

令z=p^1-2=p^-1，则（1）成为

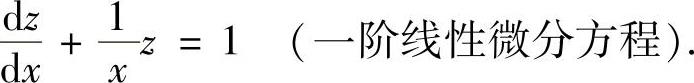
它的通解为

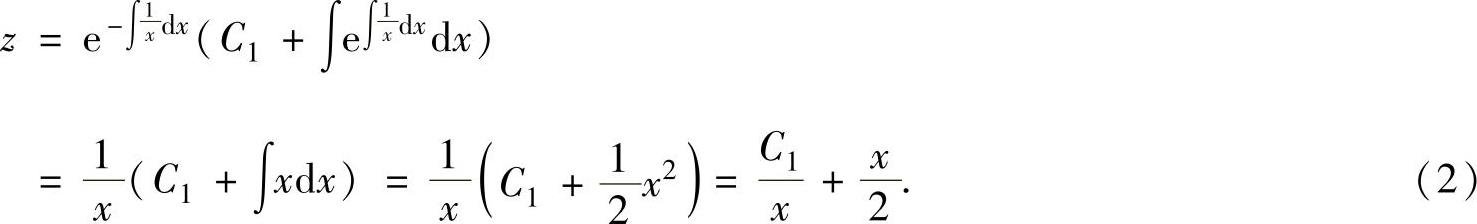
由初始条件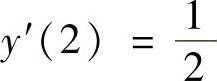得z_x=2=2，将它代入式（2）得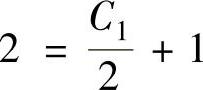，即C₁=2.所以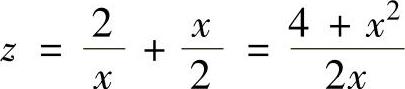，即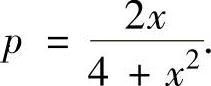

由此得到

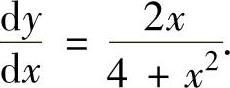
从而原微分方程的通解为

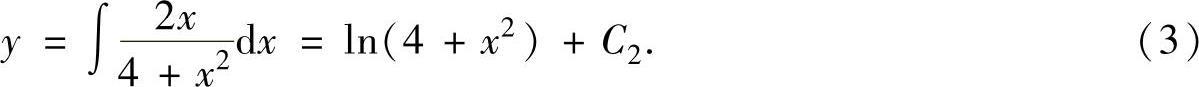
将初始条件y（2）=0代入式（3）得0=ln8+C₂，即C₂=-3ln2.所以所求微分方程的

特解为

y=ln（4+x²）-3ln2.

例4.3.3 求微分方程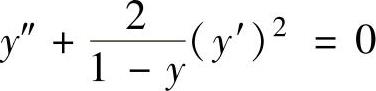的通解.

精解 所给微分方程是y″=f（y，y′）类型的二阶微分方程，令p=y′，则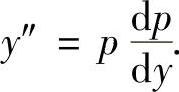将

它们代入所给的微分方程得，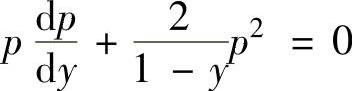

即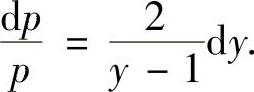

上式两边分别积分得

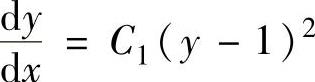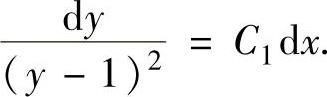lnp=2ln（y-1）+lnC₁，即p=C₁（y-1）2.由此得到，即上式两边分别积分得原微分方程的通解为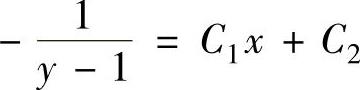，即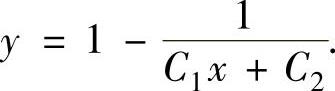

例4.3.4 求微分方程y″+（y′）2=1满足y（0）=y′（0）=0的特解.

精解 所给的微分方程是y″=f（y，y′）类型的二阶微分方程，令p=y′则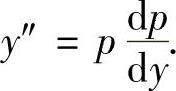将

它们代入所给的微分方程得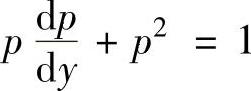，即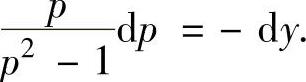

上式两边分别积分得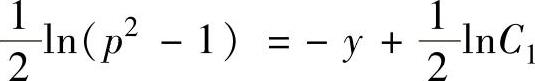，即p²=C₁e^2y+1.（1）

将y（0）=0，p（0）=y′（0）=0代入式（1）得C₁=-1.于是式（1）成为p²=1-e^-2y，即.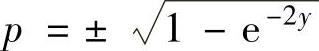

由此得到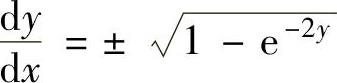，即

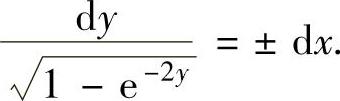
上式两边分别积分得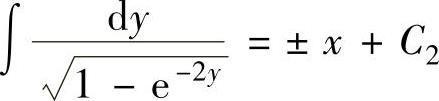，即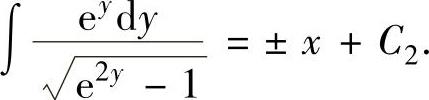

所以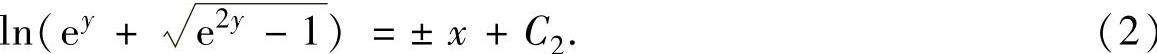

将y（0）=0代入式（2）得C₂=0.所以，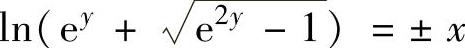

即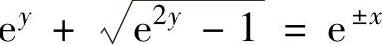，得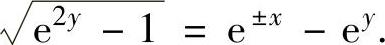

上式两边平方得e^2y_-1=e±2x-2e±xey+e²y，即

因此所求的特解为