n阶行列式的概念

一 、n阶行列式的概念

1.n阶行列式的定义

由n²个数a_ij（i=1，2，…，n；j=1，2，…，n）排成n行n列且其值为

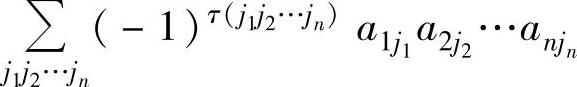
这里，j₁j₂…j_n是1，2，…，n的一个排列，τ（j₁j₂…j_n）是它的逆序数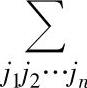，表示对1，2，…，n的所

有不同排列j₁j₂…j_n求和的记号

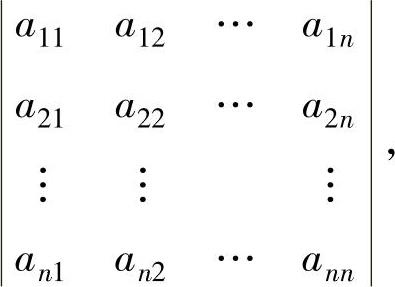
称为n阶行列式，记为D_n或D.

2.n阶行列式的性质

设D是n阶行列式，则

（1）D与它的转置行列式D^T（即将D的第i列作为第i行（i=1，2，…，n）构成的行列式）相等，即D^T=D.

（2）互换D的两行（或两列）后的行列式是D的相反数.

由此推得，当D中有两行（或两列）的元素对应相等时，D=0.

（3）用数k乘D的某行（或某列）的各个元素后的行列式等于kD.

由此推得，当D中有两行（或两列）的元素对应成比例时，D=0.

（4）如果D的某行（或某列）的各个元素都是两个数之和，则D等于相应的两个行列式之和，例如，

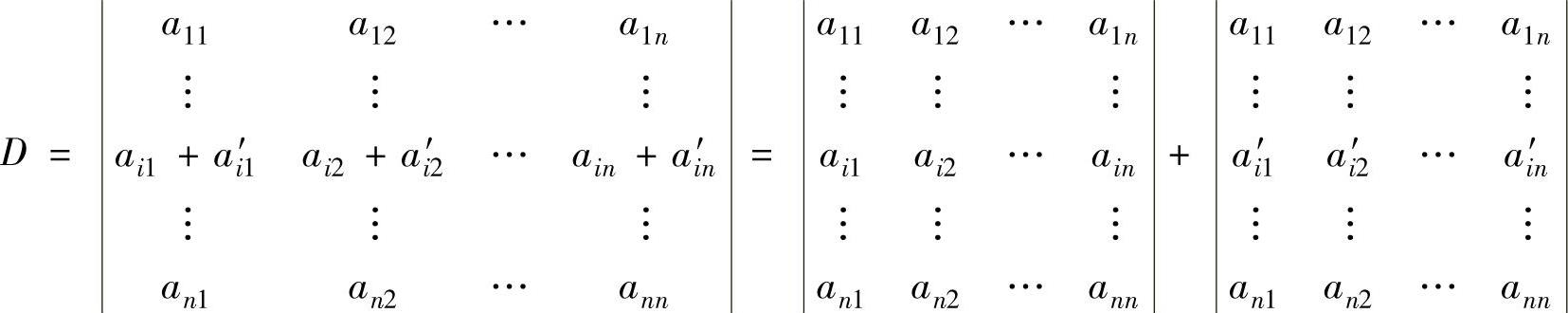
（5）将D的某行（或某列）的各个元素乘以数k加到另一行（或另一列）的对应元素后的行列式与D相等.

【典型例题】(https://www.daowen.com)

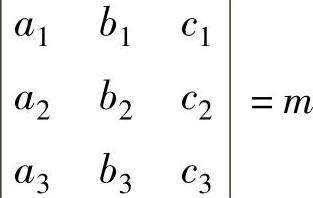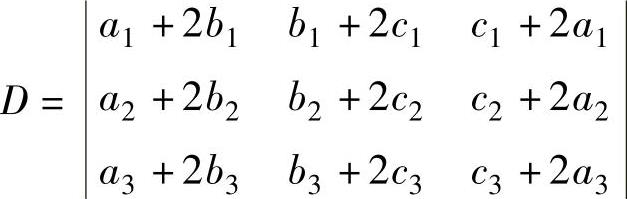例5.1.1 设三阶行列式，求的值.

精解 利用行列式性质计算D的值.

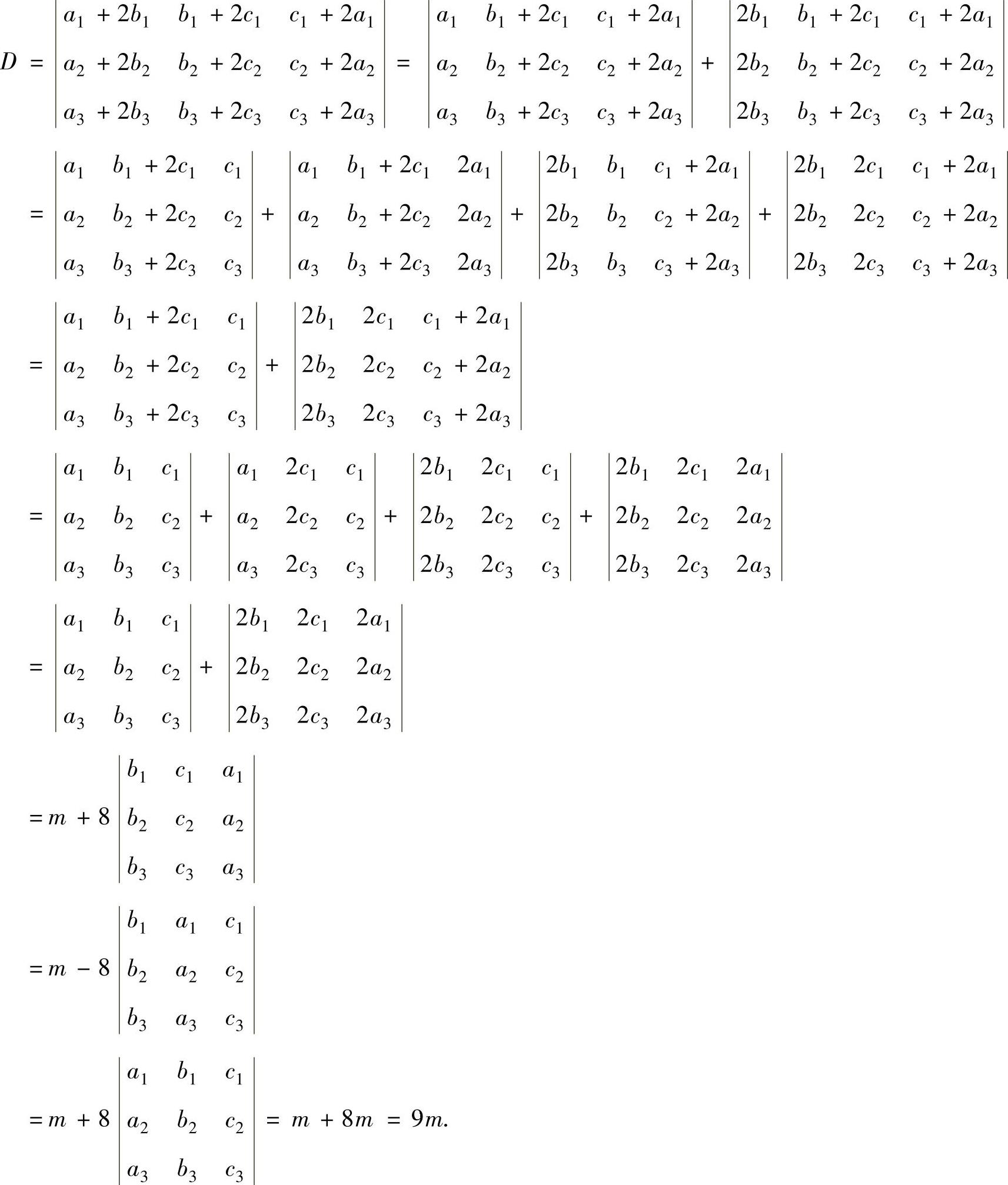
例5.1.2 计算n阶行列式

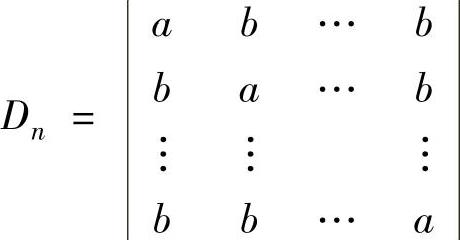
精解 利用行列式性质将D_n化为上三角行列式.

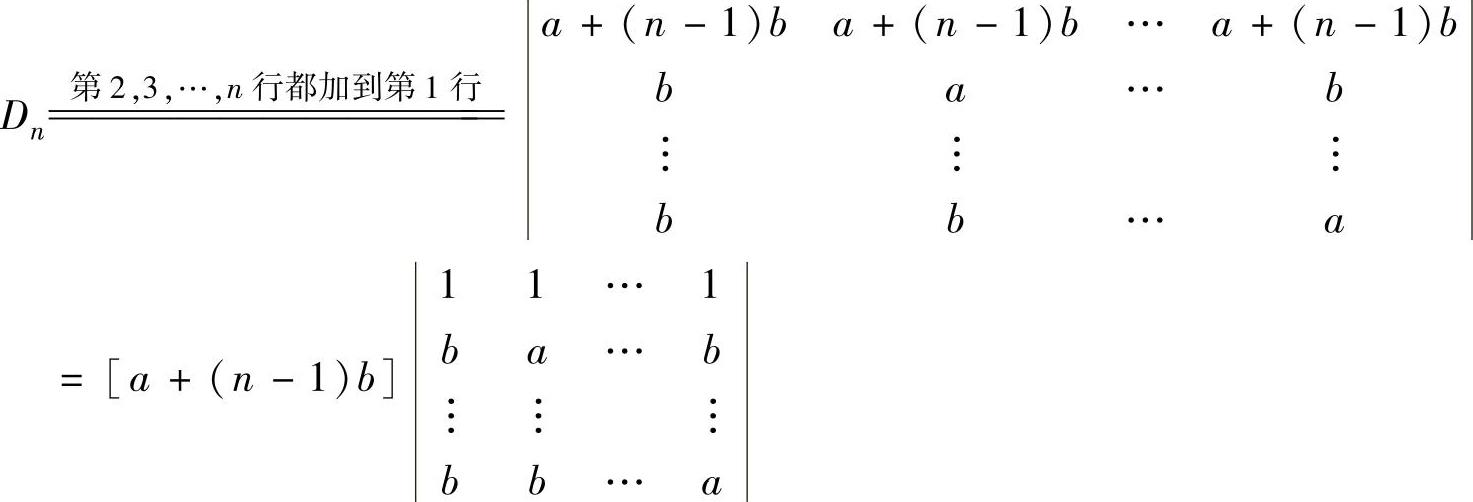
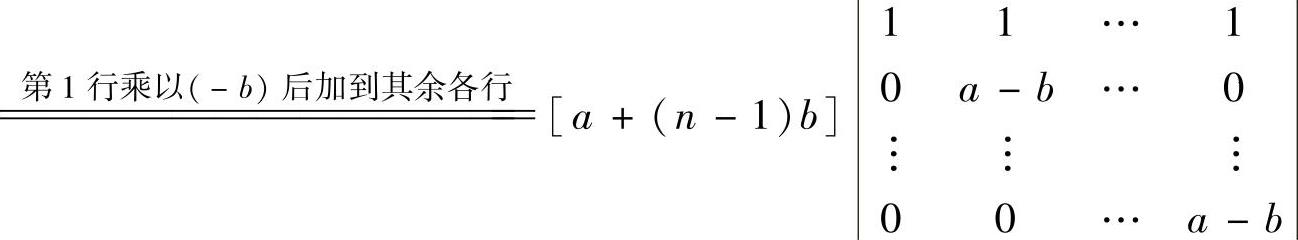
（上三角行列式）

=[a+（n-1）b]（a-b）n^-1.

注 本题的D_n在今后常会出现，应作为公式记住，即

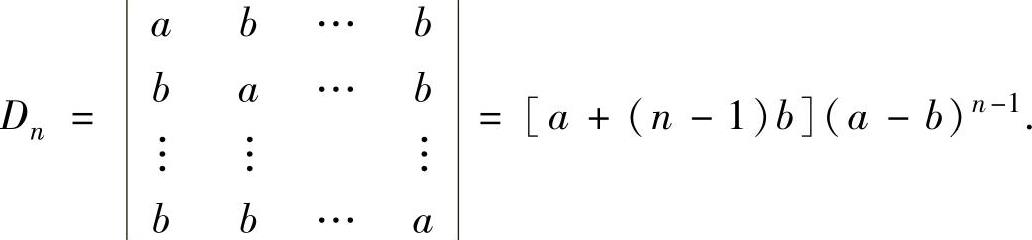
此外，还应记住n阶范德蒙德行列式

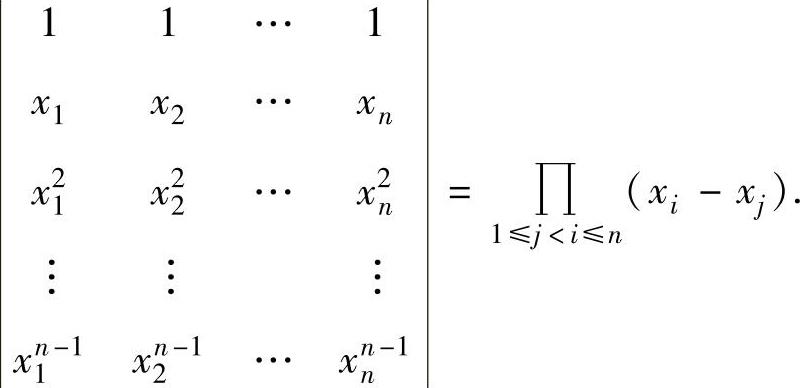
例5.1.3 计算n阶行列式

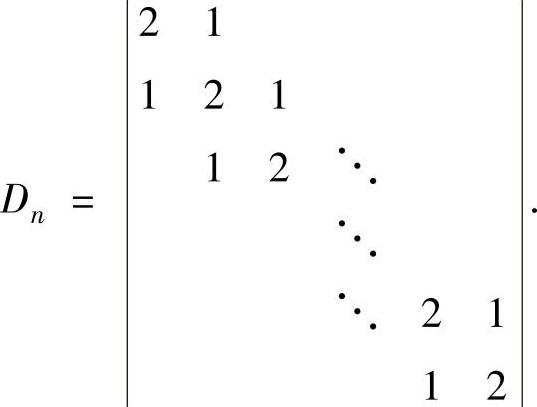
精解 利用行列式性质将D_n化为上三角行列式