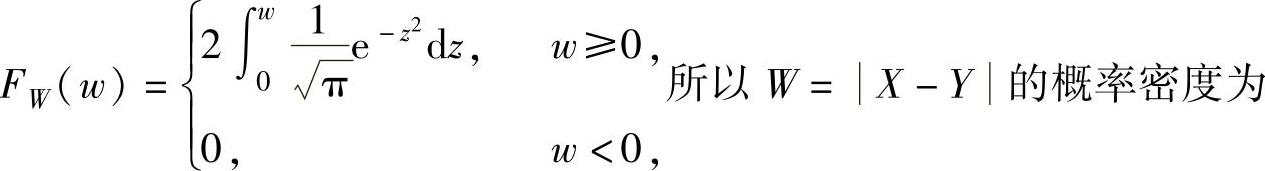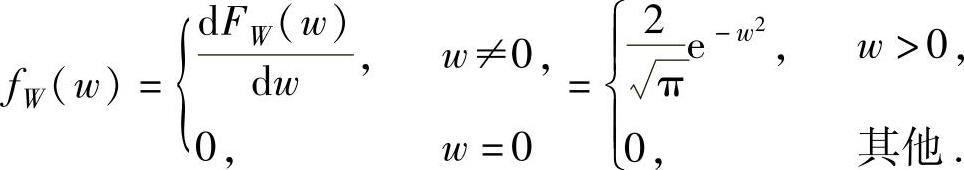二维正态分布的性质

十五 、二维正态分布的性质

【主要内容】

服从二维正态分布的随机变量有以下常用的性质：

（1）设（X，Y）～N（μ₁，μ₂，σ²₁，σ²₂，ρ），则X～N（μ₁，σ²₁），Y～N（μ₂，σ²₂）；反之，如果X与Y相互独立，且X～N（μ₁，σ²₁），Y～N（μ₂，σ²₂），则（X，Y）～N（μ₁，μ₂，σ²₁，σ²₂，0）（注意：这个结论中X与Y相互独立的条件是不可缺少的）.

（2）设（X，Y）～N（μ₁，μ₂，σ²₁，σ²₂，ρ），则对任意不全为零的常数a，b，有aX+bY～N（aμ₁+bμ₂，a²σ²₁+b²σ²₂+2abρσ₁σ₂）；特别地，当X与Y相互独立，且X～N（μ₁，σ²₁），Y～N（μ₂，σ²₂）时，对于不全为零的常数a，b，有aX+bY～N（aμ₁+bμ₂，a²σ²₁+b²σ²₂）.

（3）设（X，Y）～N（μ₁，μ₂，σ²₁，σ²₂，ρ），则X与Y相互独立的充分必要条件是ρ=0.

（4）设（X，Y）～N（μ₁，μ₂，σ²₁，σ²₂，ρ），则（Z₁，Z₂）服从二维正态分布，其中，Z₁和Z₂都是关于X，Y的线性函数，即Z₁=a₁X+b₁Y，Z₂=a₂X+b₂Y（其中a₁，a₂，b₁，b2

是常数且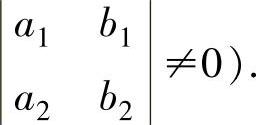

【典型例题】

例7.15.1 设随机变量X与Y相互独立，且X～N（0，1），Y～N（1，1），求概率P（X+Y≤1）与P（X-Y≤1）.

精解 利用二维正态分布的性质可以确定Z₁=X+Y与Z₂=X-Y服从正态分布，由此即可得到概率P（X+Y≤1）与P（X-Y≤1）.(https://www.daowen.com)

由于X与Y相互独立，且X，Y分别服从N（0，1）和N（1，1），所以

Z₁=X+Y～N（1×0+1×1，1²×1+1²×1）=N（1，2），

Z₂=X-Y～N（1×0+（-1）×1，1²×1+（-1）2×1）=N（-1，2），因此，，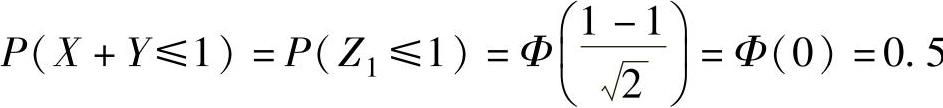

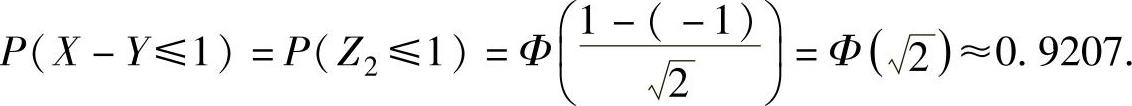
例7.15.2 设随机变量X与Y相互独立，且都服从正态分布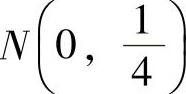，求随机变量W=X-Y的概率密度.

精解 先确定Z=X-Y所服从的正态分布，然后通过计算随机变量W=Z的分布函数算出W的概率密度f_W（w）.

由于X与Y相互独立，且都服从正态分布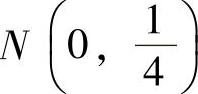，所以Z=X-Y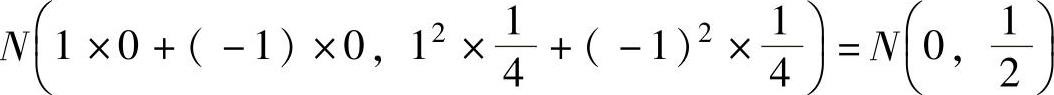～，因此Z的概率密度为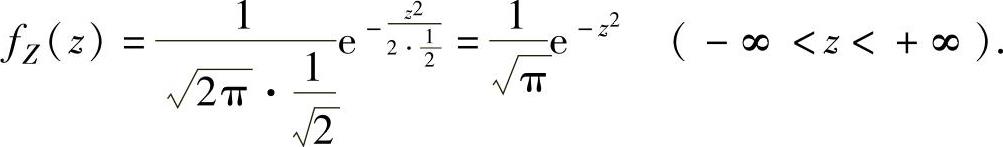

设W=Z的分布函数为F_W（w），则由分布函数的定义知

F_W（w）=P（W≤w）=P（Z≤w）.下面计算上式右边的概率：

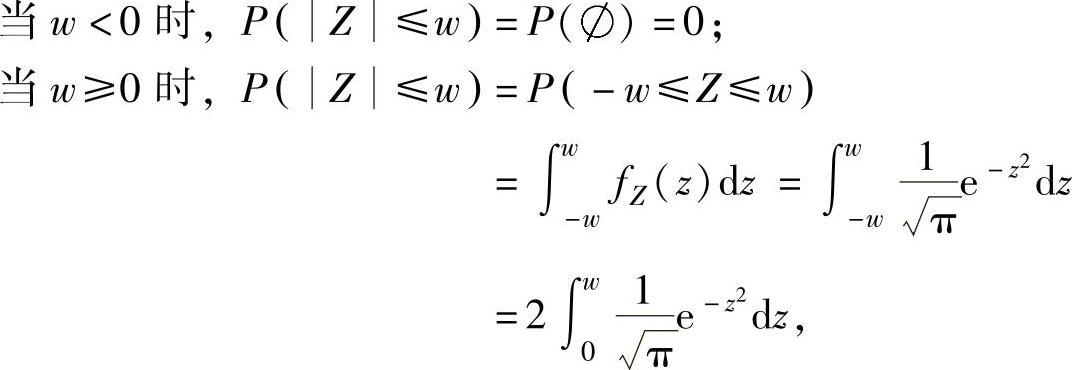
即