随机变量的协方差与相关系数
【主要内容】
1.随机变量协方差的定义与性质
设（X，Y）是二维随机变量.如果E[（X-EX）（Y-EY）]存在，则称Cov（X，Y）=E[（X-EX）（Y-EY）]为X与Y的协方差.
协方差有以下性质：设X，X1，X2，Y是随机变量，则
（1）Cov（X，Y）=Cov（Y，X）；
（2）Cov（X，c）=0（其中c是常数）；
（3）Cov（c1X，c2Y）=c1c2Cov（X，Y）（其中，c1，c2是常数）；
（4）Cov（X1+X2，Y）=Cov（X1，Y）+Cov（X2，Y）；
（5）当X与Y相互独立时，Cov（X，Y）=0；
（6）D（X±Y）=DX+DY±2Cov（X，Y）；
（7）Cov（X，Y）=E（XY）-EX·EY（协方差可以按定义计算，但在许多场合下按这个公式计算）.
2.随机变量相关系数的定义与性质设（X，Y）是二维随机变量，如果DX>0，DY>0，则称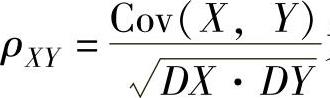
为X与Y的相关系数，相关系数ρXY有以下性质：
（1）ρXY≤1；
（2）ρXY=1的充分必要条件是存在常数a，b，使得P（Y=aX+b）=1，特别地，当ρXY=1时，称X与Y正相关，此时上述的a>0；当ρXY=-1时，称X与Y负相关，此时上述的a<0.
3.随机变量相关性的定义
设（X，Y）是二维随机变量.如果X与Y的相关系数ρXY=0，则称X与Y不相关；否则称为相关.
随机变量X与Y的相关性与独立性有以下的关系：
（1）当X与Y相互独立，且DX>0，DY>0时，X与Y不相关；
（2）当X与Y不相关时，X与Y未必相互独立；
（3）当X与Y不独立时，且DX>0，DY>0时，X与Y未必相关；
（4）当X与Y相关时，X与Y不独立.
特别地，当（X，Y）～N（μ1，μ2，σ21，σ22，ρ）时，X与Y的相关系数ρXY=ρ，并且
（1）X与Y不相关的充分必要条件是ρ=0；
（2）X与Y不相关与独立等价.
【典型例题】
例7.18.1（单项选择题）设随机变量X～N（0，1），Y～N（1，4），且X与Y的相关系数ρXY=1，则（ ）.
A.P（Y=-2X-1）=1 B.P（Y=-2X+1）=1
C.P（Y=2X-1）=1 D.P（Y=2X+1）=1
精解 由ρXY=1知X与Y正相关，即Y=aX+b，使得P（Y=aX+b）=1，a>0.所以选项A和B都不能选.此外，对选项C，EY=E（2X-1）=-1，这与题设EY=1矛盾，所以选项C也不能选.
因此本题选D.
例7.18.2 （单项选择题）设随机变量X，Y都服从正态分布，且它们不相关，则（ ）.
A.X与Y一定独立 B.（X，Y）服从二维正态分布
C.X与Y未必独立 D.X+Y服从正态分布
精解 由X与Y都服从正态分布未必能推出（X，Y）服从二维正态分布，所以，虽然X与Y不相关，但X与Y未必独立.
因此本题选C.
例7.18.3 （单项选择题）将一枚硬币重复掷n次，用X和Y来分别表示正面向上和反面向上的次数，则X与Y的相关系数为（ ）.
A.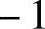
B.0C.
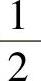D.1
精解 按相关系数的定义计算，即先算出DX，DY以及Cov（X，Y）.
由于X和Y都服从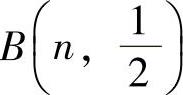
，其中Y=n-X，所以
，
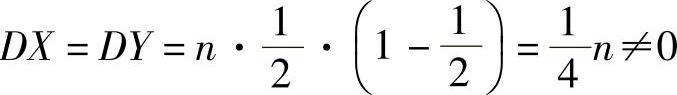Cov（X，Y）=Cov（X，n-X）=-Cov（X，X）=-DX.
从而X与Y的相关系数为
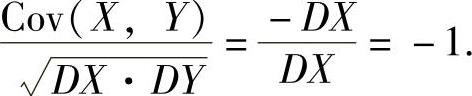
因此本题选A.
例7.18.4 设随机变量X～N（1，32），Y～N（0，22），且X与Y的相关系数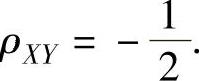
记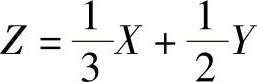
，求X与Z的相关系数ρXZ.
精解 按相关系数的定义计算，即先算出DX，DZ以及Cov（X，Z）.由于DX=9，DY=4，
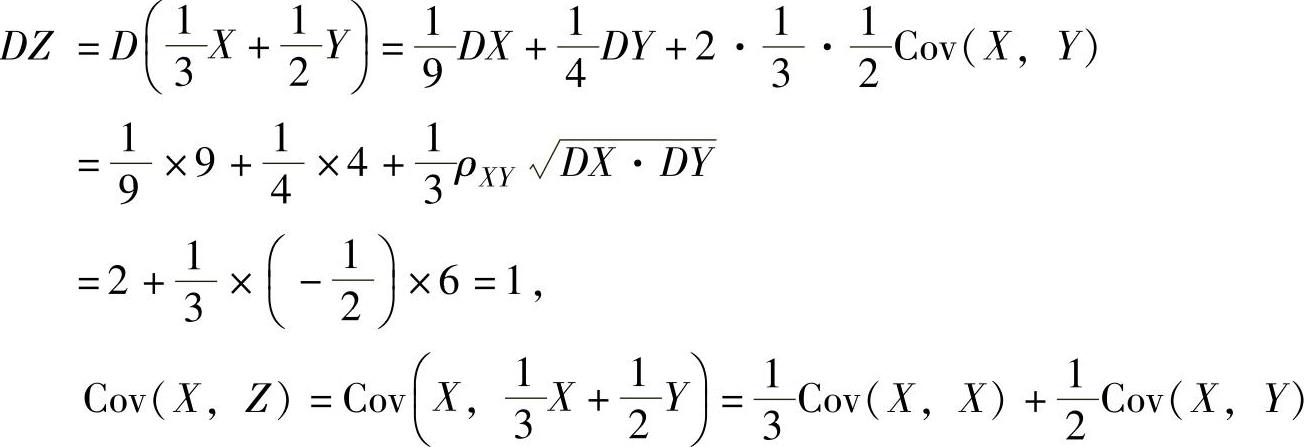
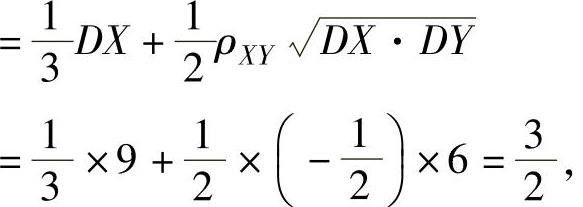
所以，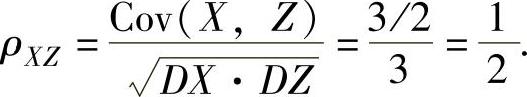
例7.18.5 设二维随机变量（X，Y）的概率密度为
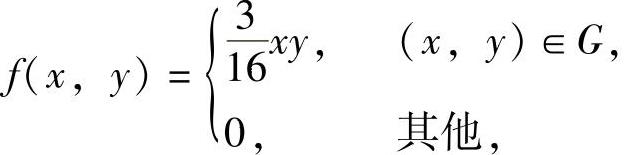
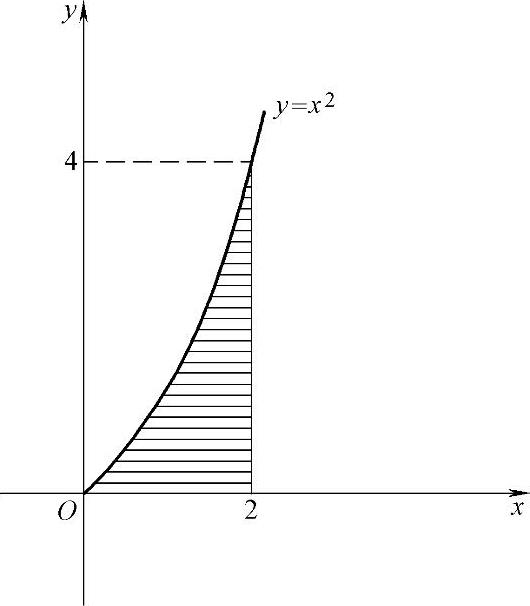
图 7.18.5
其中G={（x，y）0≤x≤2，0≤y≤x2}（如图7.18.5中的阴影部分所示），求Cov（X，Y）.
精解 利用公式Cov（X，Y）=E（XY）-EX·EY计算Cov（X，Y），为此先算出EX，EY以及E（XY）.
分别记（X，Y）的关于X和关于Y的边缘概率密度为fX（x），fY（y），则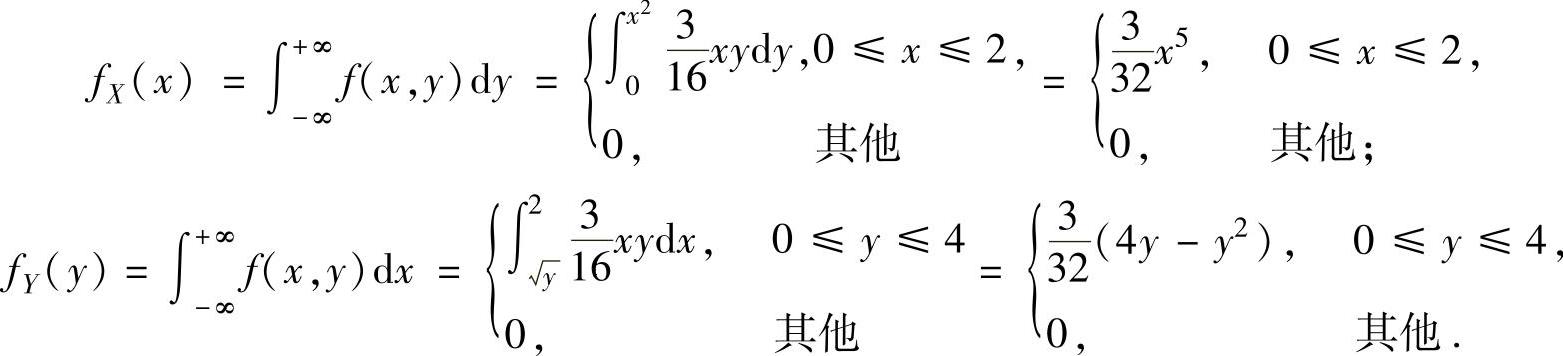
所以，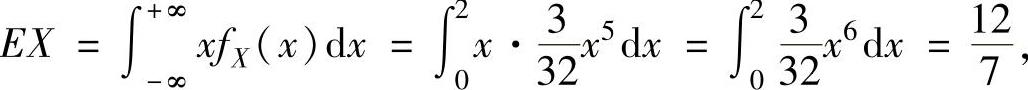
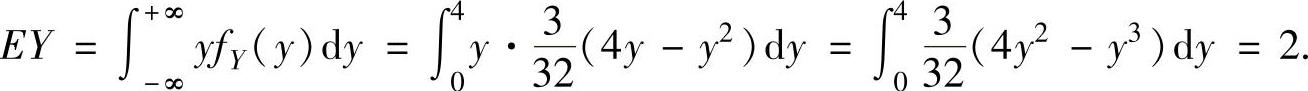
此外，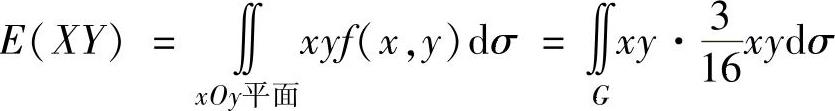
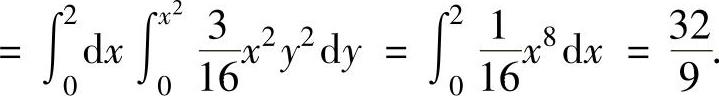
于是