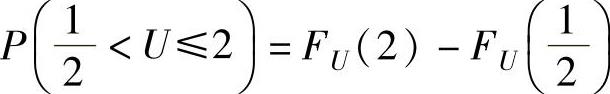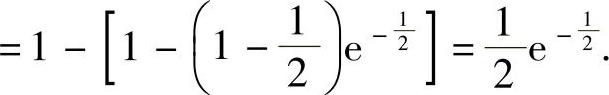二元随机变量函数的分布

十四 、二元随机变量函数的分布

【主要内容】

1.二元随机变量函数分布的计算

设（X，Y）是二维随机变量，g（x，y）是已知函数，则称随机变量Z=g（X，Y）为两个随机变量的函数.

当（X，Y）是二维离散型随机变量，其分布列为P（X=x_i，Y=y_j）=p_ij（i=1，2，…，m，…；j=1，2，…，n，…）时，Z=g（X，Y）的分布律为

这里z₁，z₂，…，zk，…确定如下：对每对（x_i，y_j）算出g（x_i，y_j）的值，然后将它们整合，即相同的只保留一个，并作由小到大的排列.此外，

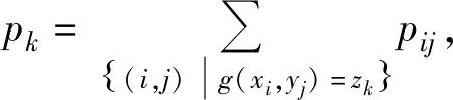
由此可以进一步算出Z的分布函数F_Z（z）.

当（X，Y）是二维连续型随机变量，其概率密度为f（x，y）时，随机变量Z=g（X，Y）的分布函数F_Z（z）与概率密度f_Z（z）可按以下方法计算：

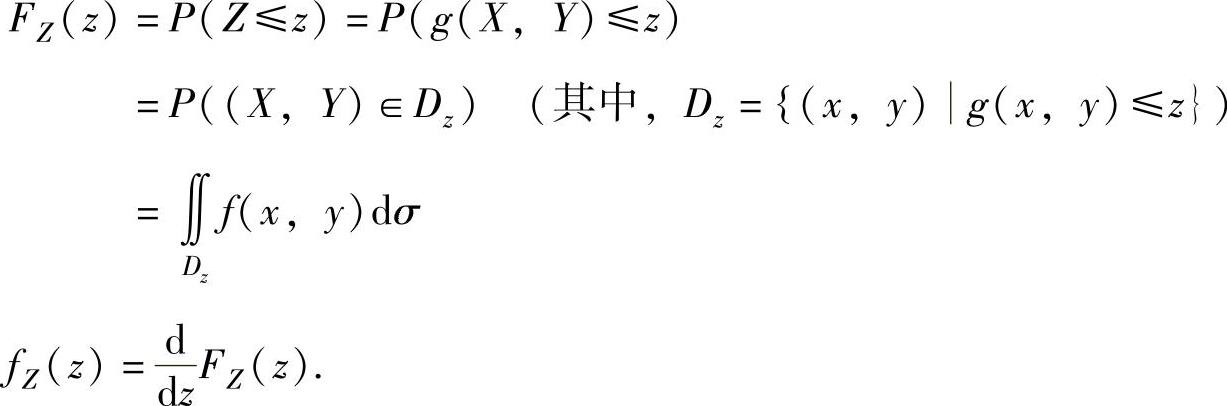
2.常见的两个随机变量函数的分布

（1）设（X，Y）是二维连续型随机变量，其概率密度为f（x，y），则随机变量Z=aX+bY+c（a，b，c是常数）的概率密度f_Z（z）为

当b≠0时，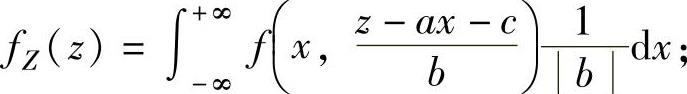

当a≠0时，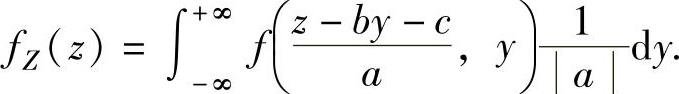

注 （ⅰ）当Z=X+Y时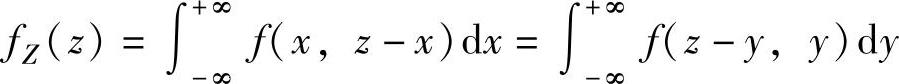，，特别地，当

X与Y相互独立时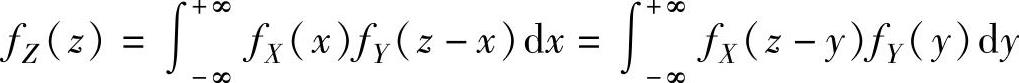，（其中，f_X（x）和f_Y（y）分别是X和

Y的概率密度）.

（ⅱ）当Z=X-Y时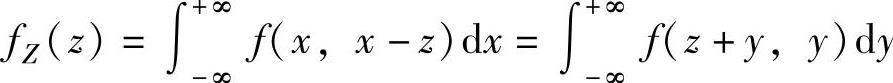，y，特别地，当X与

Y相互独立时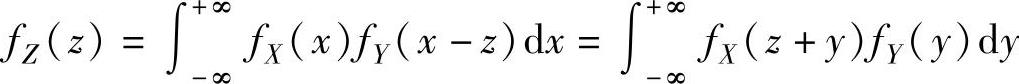，（其中，f_X（x）和f_Y（y）分别是X和

Y的概率密度）.

（2）设X与Y相互独立，它们的分布函数分别为F_X（x）与F_Y（y），则随机变量Z₁=max{X，Y}与Z₂=min{X，Y}的分布函数分别为

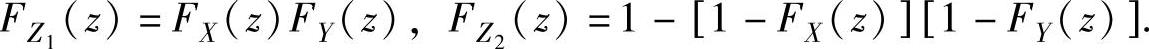
【典型例题】

例7.14.1 设随机变量X与Y相互独立，它们的分布律分别为

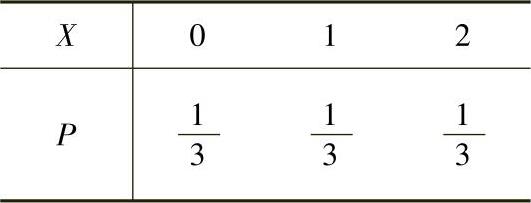
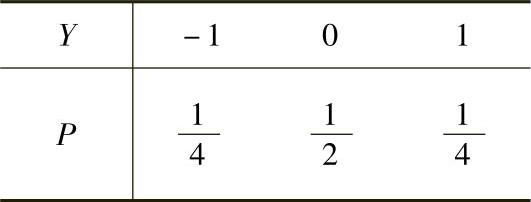
求随机变量Z=X+2Y的分布律.

精解 先写出（X，Y）的分布律，然后据此确定Z的分布律.

由于X与Y相互独立，所以（X，Y）的分布律为

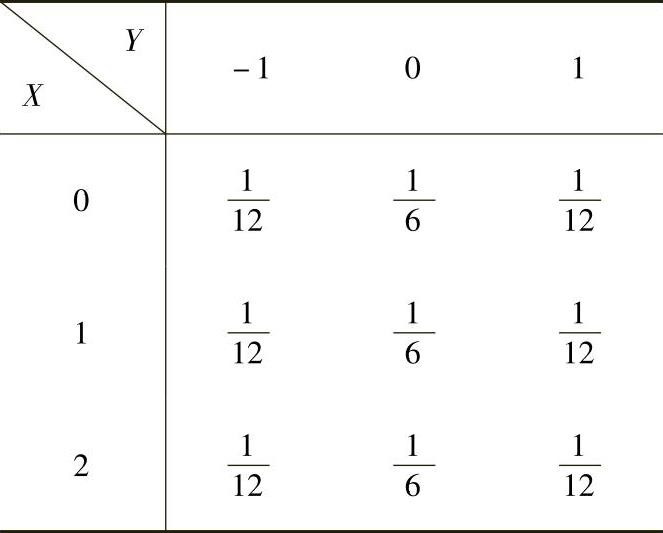
由上表可知Z=X+2Y全部可能取的值为-2，-1，0，1，2，3，4，并且对应的概率为，，，，，，，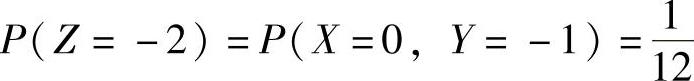

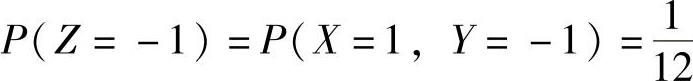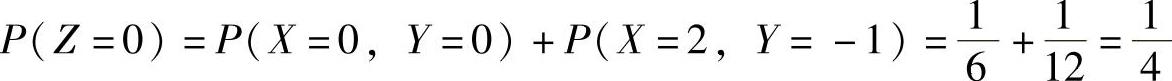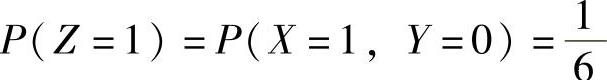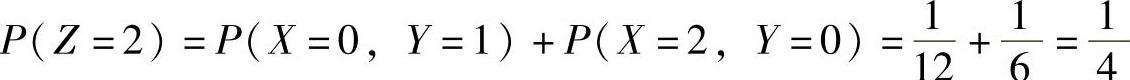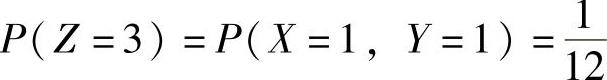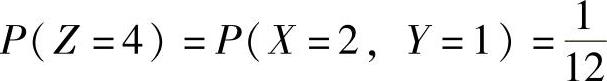因此Z=X+2Y的分布律可列表表示为

例7.14.2 设随机变量（X，Y）的概率密度为

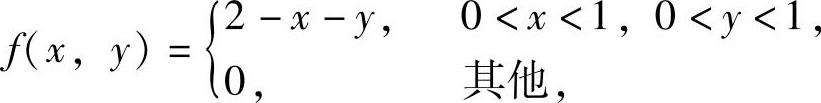
求随机变量Z=X+Y的概率密度f_Z（z）.

精解 按Z=X+Y的概率密度计算公式计算f_Z（z），即

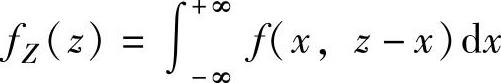(https://www.daowen.com)

，

其中，，，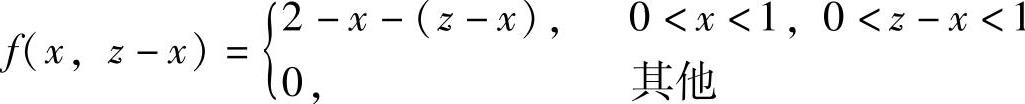

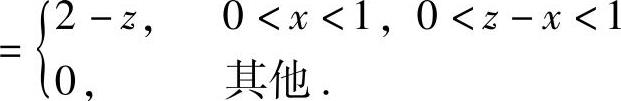由此可知，f（x，z-x）在D={（x，z）0<x<1，0<z-x<1}（如图7.14.2阴影部分所示）上取值为2-z，在xOz平面的其他部分取值都为零.

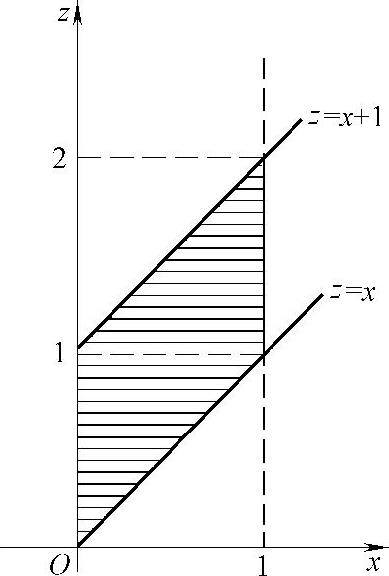
图 7.14.2

当0≤z<1时，，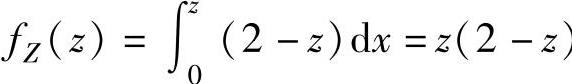

当1≤z≤2时，，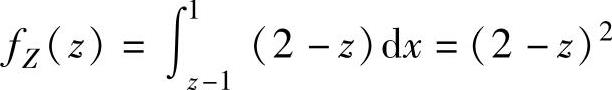

当z<0或z>2时，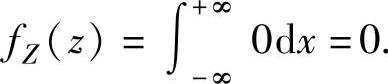

因此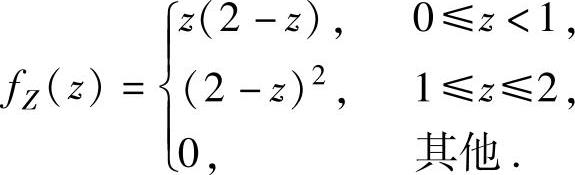

例7.14.3 设二维随机变量（X，Y）的概率密度为

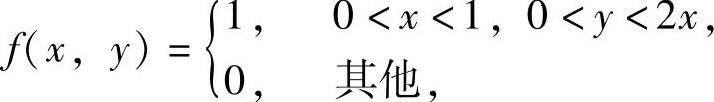
求随机变量Z=2X-Y的概率密度f_Z（z）.

精解 按Z=2X-Y的概率密度计算公式计算f_Z（z），即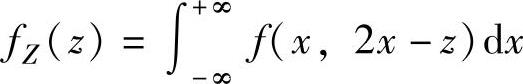，其中，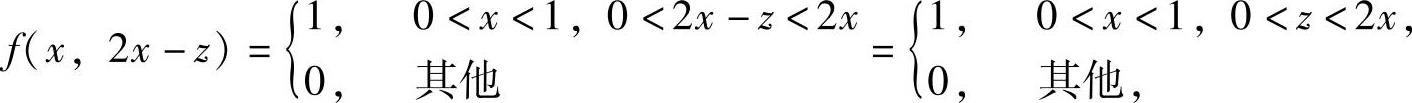

即f（x，2x-z）在D={（x，z）0<x<1，0<z<2x}（如图7.14.3阴影部分所示）上取值为1，在xOz平面的其他部分上取值为零.

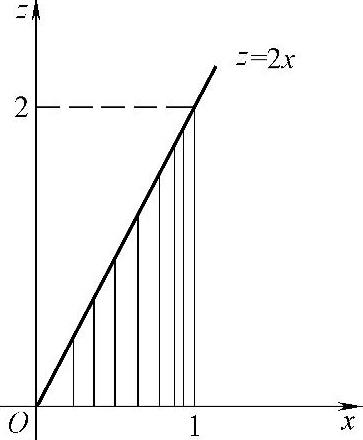
图 7.14.3

当0≤z≤2时，

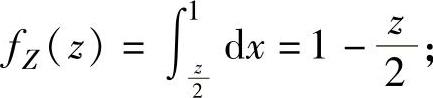
当z<0或z>2时，

，

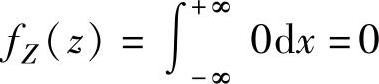
即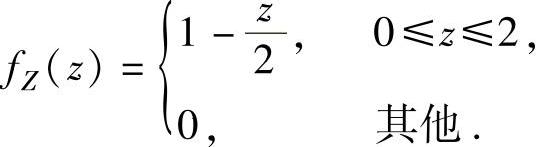

例7.14.4 设随机变量X与Y相互独立，X～E（1），Y～U[0，1].

（1）求随机变量Z=max{X，Y}的概率密度f_Z（z）；

（2）记U=min{X，Y}，求概率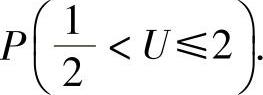

精解 （1）先算Z的分布函数F_Z（z），然后求导得到f_Z（z）.

由于X与Y相互独立，所以F_Z（z）=F_X（z）F_Y（z），（1）

其中，由X的概率密度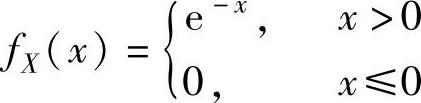，得X的分布函数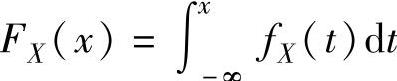

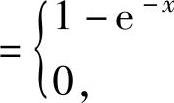
，x>0

{_x≤0，从而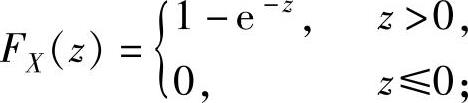由Y的概率密度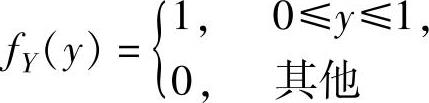

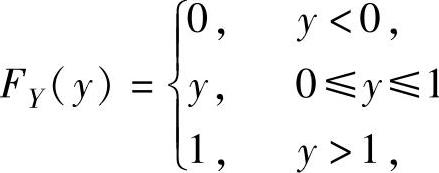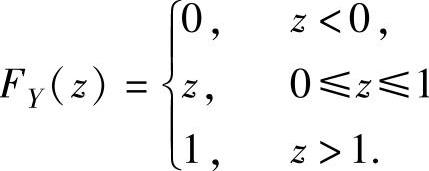得Y的分布函数，从而，所以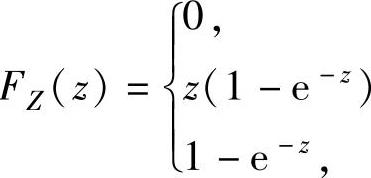

z<0，，0≤z≤1，

z>1.

由此得到，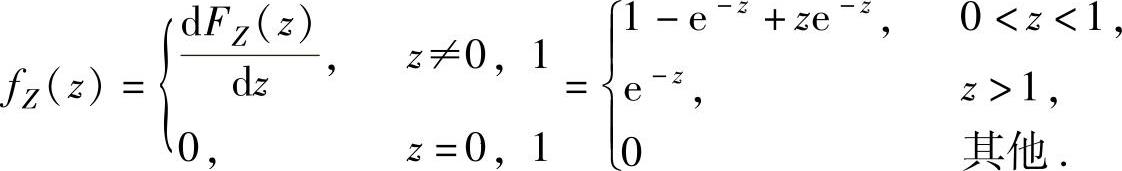

（2）先计算U的分布函数F_U（u），然后由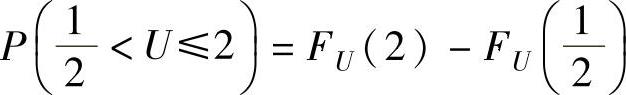算出这个概

率.由于U=min{X，Y}的分布函数

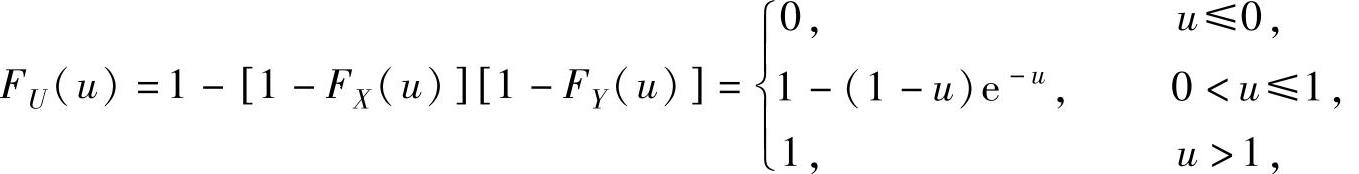
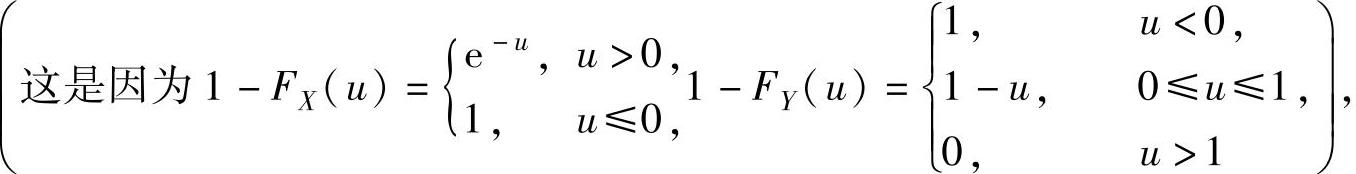
所以，