伴随矩阵与矩阵求逆运算
【主要内容】
1.伴随矩阵
设A是n阶矩阵,则称
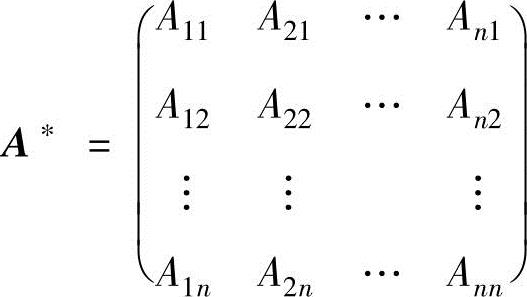
为A的伴随矩阵,其中,Aij是|A|的元素aij的代数余子式(i,j=1,2,…,n).
伴随矩阵的性质:设A,B都是n阶矩阵,则
(1)A∗A=AA∗=|A|En;
(2)|A∗|=|A|n-1(n>1);
(3)(λA)∗=λn-1A∗(其中,λ是常数);
(4)(AT)∗=(A∗)T;
(5)(AB)∗=B∗A∗;
(6)设M1,M2都是方阵,则

2.矩阵求逆运算
设A是n阶矩阵,如果存在n阶矩阵B,使得AB=BA=En,则称A是可逆矩阵(简称A可逆),B是A的逆矩阵.由于A的逆矩阵是唯一的,记为A-1.由矩阵A产生矩阵A-1的运算,称为矩阵的求逆运算,简称求逆.
可逆矩阵的性质:设A,B都是n阶矩阵,则
(1)A可逆的充分必要条件为|A|≠0.
(2)如果A可逆,则A-1也可逆,且(A-1)-1=A.
(3)如果A可逆,常数λ≠0,则λA可逆,且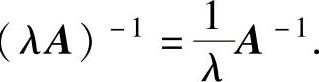
(4)如果A,B都可逆,则AB可逆,且(AB)-1=B-1A-1.
(5)如果A可逆,则AT可逆,且(AT)-1=(A-1)T.
(6)如果A可逆,则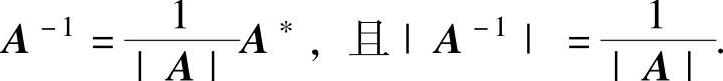
(7)如果A可逆,则A↔En.
(8)如果A可逆,则A∗可逆且(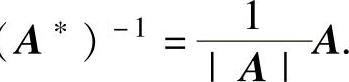
(9)当M1,M2可逆时有
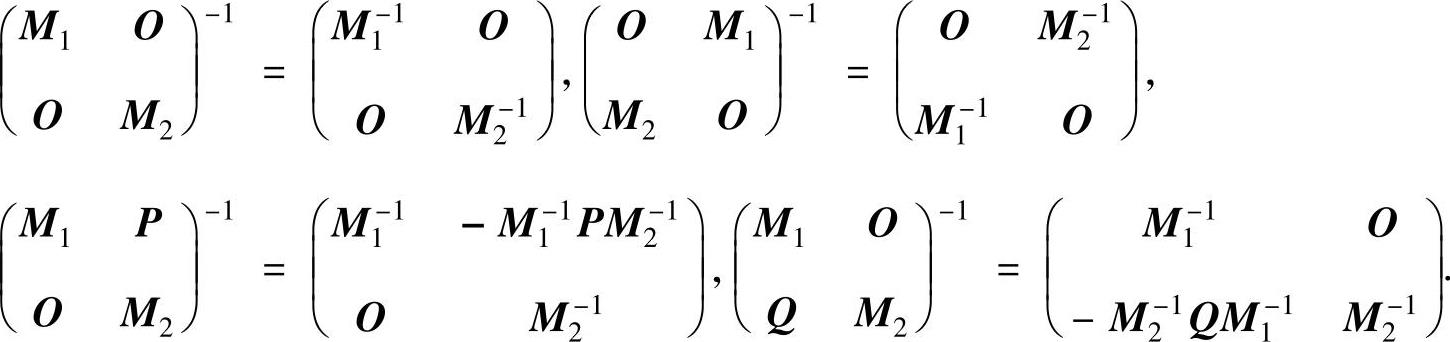
(10)初等矩阵是可逆矩阵,且
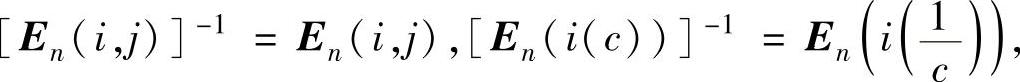
[En(i,j(k))]-1=En(i,j(-k)),[En(i(k),j)]-1=En(i(-k),j).
3.求逆方法
(1)伴随矩阵法
设A是可逆矩阵,则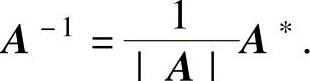
(2)初等变换法
设A是n阶矩阵,如果对矩阵(A︙En)施行一系列初等行变换成为(En︙B),则A-1=B.
【典型例题】
例5.5.1 设A是n阶矩阵,a是非零常数.记B是A的第i行的每个元素都乘以a后的矩阵,试用A∗表示B∗.
精解 利用伴随矩阵性质求解.
由题设知 B=En(i(a))A,所以
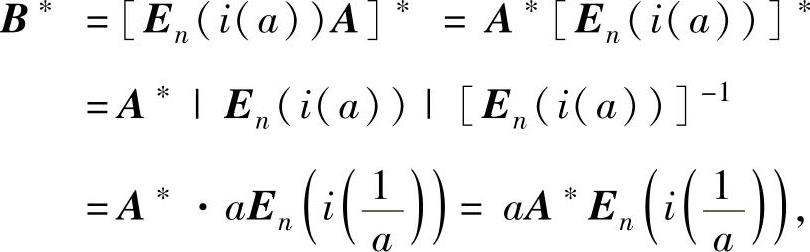
即B∗是矩阵A∗的除第i列外,每个元素都乘以a的矩阵.
例5.5.2 (单项选择题)设矩阵
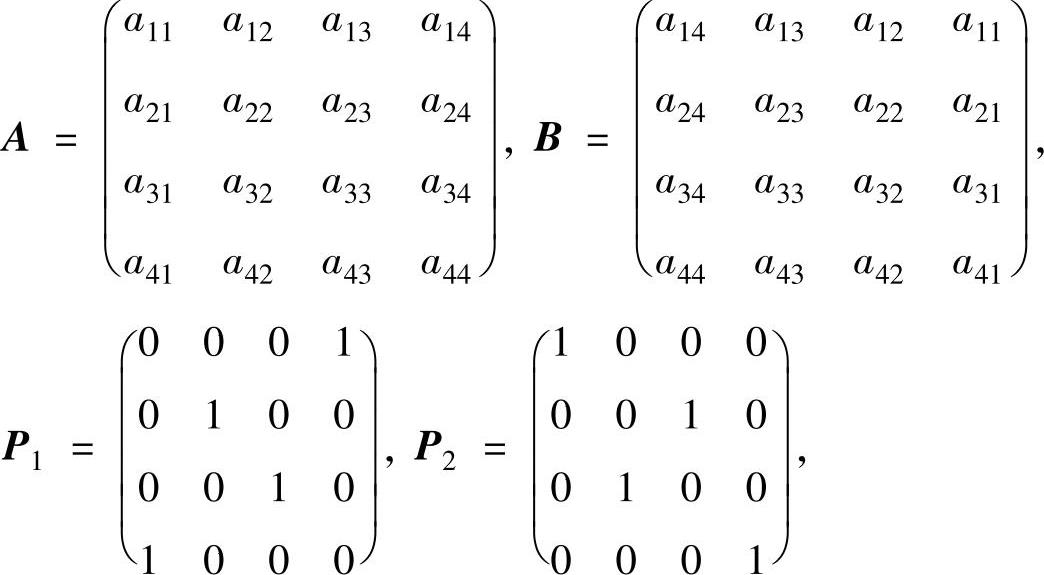
其中,A可逆,则B-1=( ).(https://www.daowen.com)
A.A-1P1P2 B.P1A-1P2 C.P1P2A-1 D.P2A-1P1
精解 互换A的第2列与第3列后再互换第1列与第4列得到B,所以B=AP2P1,从而由可逆矩阵性质得
B-1=(AP2P1)-1=P1-1P2-1A-1=P1P2A-1.
因此本题选C.
例5.5.3 (单项选择题)设A是n(n≥2)阶可逆矩阵,交换A的第1行与第2行得到矩阵B,且A∗,B∗分别为A,B的伴随矩阵,则( ).
A.交换A∗的第1、2列得到B∗
B.交换A∗的第1、2行得到B∗
C.交换A∗的第1、2列得到-B∗
D.交换A∗的第1、2行得到-B∗
精解 通过确定B∗的关于A∗的表达式得到正确的选项.
由 B=En(1,2)A 得
B∗=[En(1,2)A]∗=A∗[En(1,2)]∗=A∗·|En(1,2)|[En(1,2)]-1
=A∗·(-1)En(1,2)(由于|En(1,2)|=-1,[En(1,2)]-1=En(1,2))
=-A∗En(1,2),
即A∗En(1,2)=-B∗,
因此本题选C.
例5.5.4 设四阶矩阵
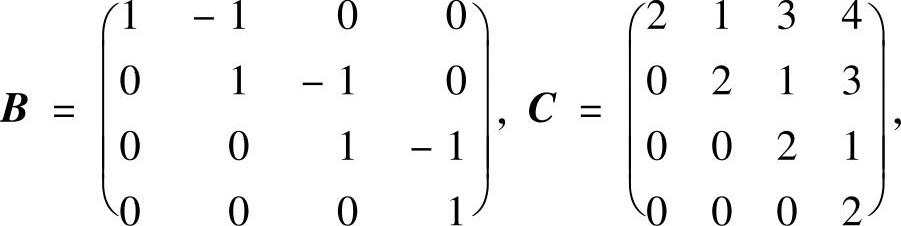
求[(E4-C-1B)TCT]-1.
精解 先利用转置矩阵与可逆矩阵的有关性质化简矩阵式(E4-C-1B)TCT,然后再计算它的逆矩阵.由于
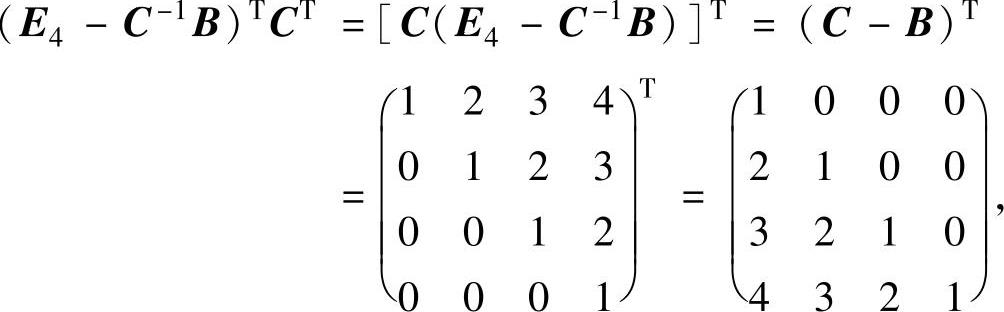
所以
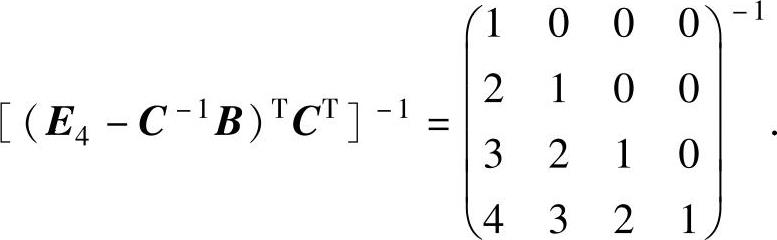
可以利用初等变换法计算上述矩阵的逆矩阵:由于
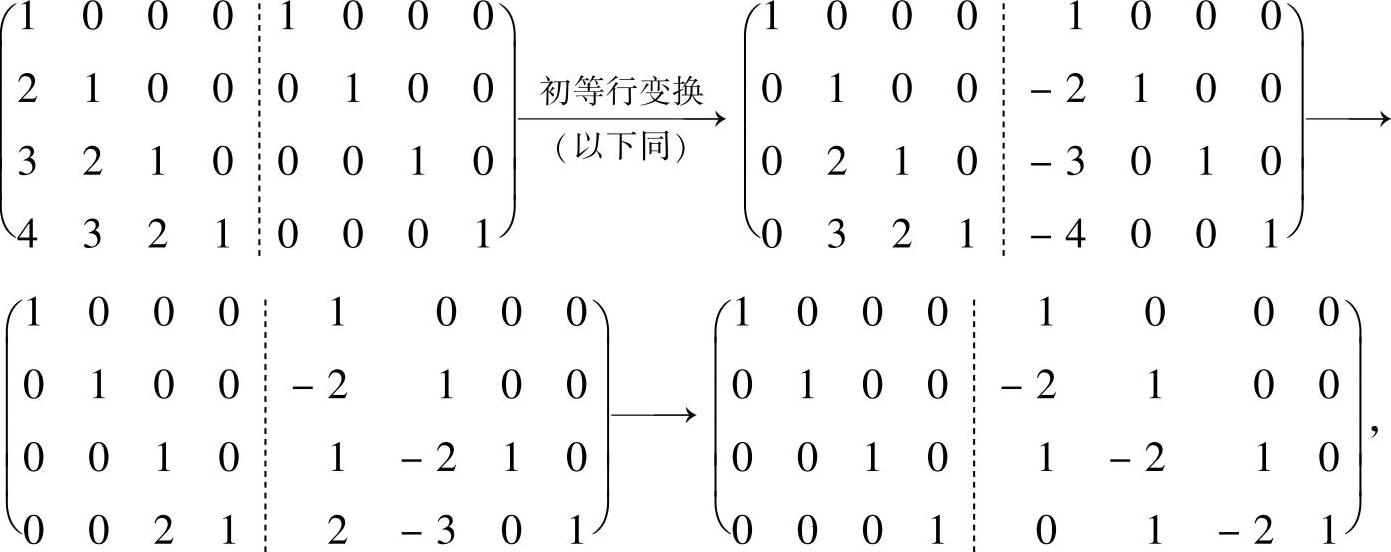
所以,
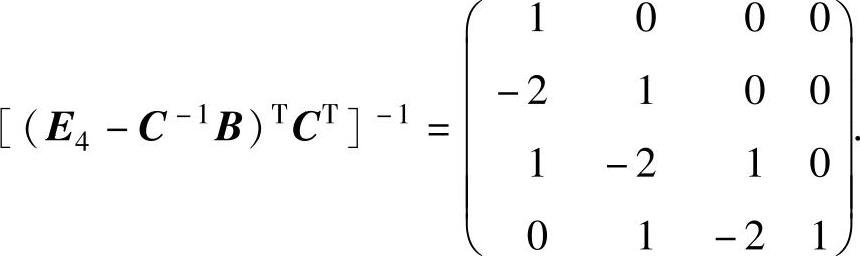
例5.5.5 设三阶矩阵
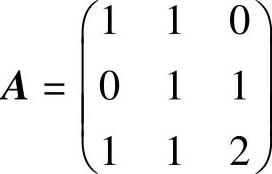
,求行列式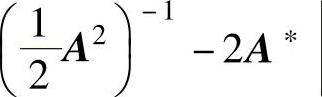 的值,其中,A∗是
的值,其中,A∗是
A的伴随矩阵.
精解 先化简矩阵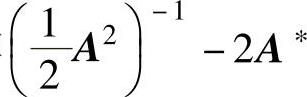 ,然后计算它的行列式.
,然后计算它的行列式.
容易算出|A|=2.由于
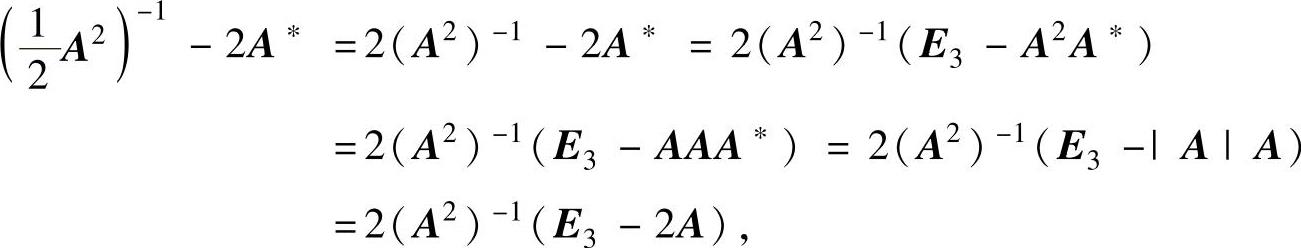
所以,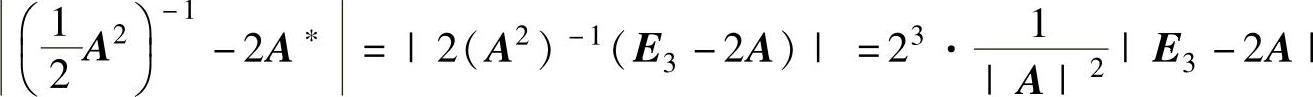
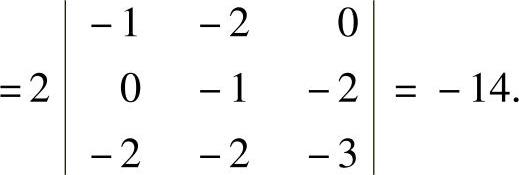
例5.5.6 已知n阶矩阵A=(aij),B=(bij)都可逆,且
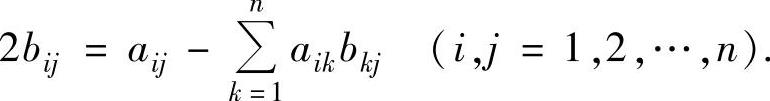
证明:矩阵B-En可逆,并求(B-En)-1.
精解 只要证明存在n阶矩阵C,使得C(B-En)=En即可.
由题设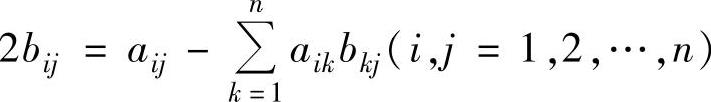 得2B=A-AB,即2(B-En)+A(B-En)=-2En.
得2B=A-AB,即2(B-En)+A(B-En)=-2En.
由此得到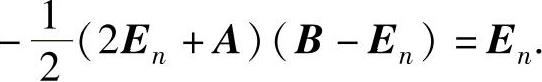 因此B-En可逆,且
因此B-En可逆,且
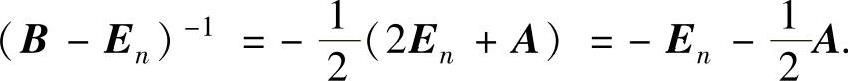
注 当M是n阶矩阵时,欲证其可逆,只要证明存在矩阵P使
PM=En或MP=En即可.
