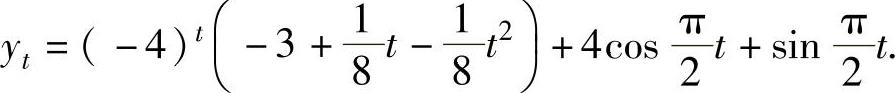一阶常系数线性差分方程

七、一阶常系数线性差分方程

【主要内容】

设a是非零常数，f（t）是已知函数，则称y_t+1+ay_t=f（t）（t=0，1，2，…）（∗）

（这里y_t=φ（t）是未知函数）为一阶常系数线性差分方程.当自由项f（t）≡0时，式（∗）成为y_t+1+ay_t=0（t=0，1，2，…）.

上式就是式（∗）对应的一阶常系数齐次线性差分方程.（∗∗）

如果函数y_t=φ（t）代入式（∗）或（式（∗∗）），使之对t=0，1，2，…成为恒等式，则称y_t=φ（t）是式（∗）或（∗∗）的解.式（∗）（或（∗∗））的包含有一个任意常数的解，称为式（∗）（或（∗∗））的通解；当通解中的任意常数被初始条件y₀=A确定时的解，称为特解.

式（∗）的通解为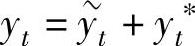，其中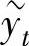是式（∗∗）的通解，y_t∗是式（∗）的特解.

1.一阶常系数齐次线性差分方程的通解（其中C是任意常数）.

2.一阶常系数非齐次线性差分方程的特解

（1）当f（t）=d^t·P_n（t）（其中P_n（t）是已知的n次多项式，d是非零常数）时，式（∗）有特解

y_t∗=t^k·d^tQ_n（t）.其中，k=0，a+d≠0，

{₁，a+d=0，Q_n（t）是待定的n次多项式，它的系数可通过将y_t∗代入式（∗）确定.

（2）当f（t）=b₁cosωt+b₂sinωt（其中ω≠0，且b₁，b₂是不同时为零的常数）时，式（∗）有特解

y_t∗=t^k（αcosωt+βsinωt），

其中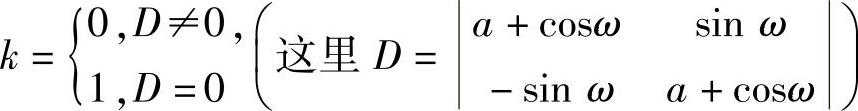，，α，β为待定常数，可将y_t∗代入式（∗）确

定.

注设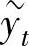和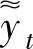分别是一阶常系数非齐次线性差分方程y_t+1+ay_t=f₁（t）和y_t+1+ay_t=

f₂（t）的特解，则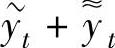是y_t+1+ay_t=f₁（t）+f₂（t）的特解.

【典型例题】

例4.7.1 求差分方程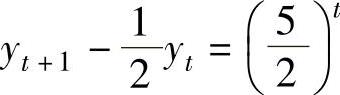的通解.

精解 所给差分方程是一阶常系数非齐次线性差分方程，它对应的齐次线性差分方程为

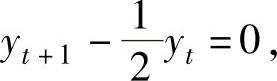
(https://www.daowen.com)

其通解为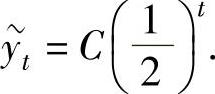而所给的差分方程应有形如

的特解.将它代入所给的差分方程得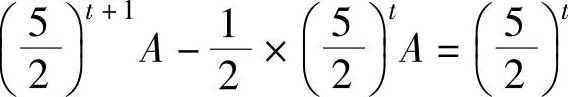，即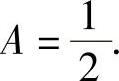

将它代入式（1）得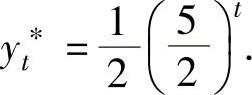于是所给的差分方程的通解为

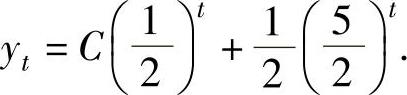
例4.7.2 求差分方程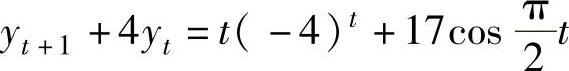满足y₀=1的特解.

精解 所给差分方程是一阶常系数非齐次线性差分方程，它对应的齐次线性差分方程为

y_t+1⁺⁴y_t=0，

其通解为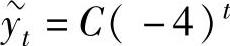，而所给的差分方程应有形如

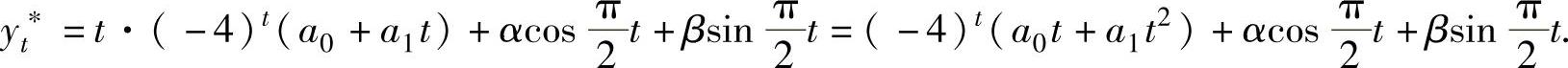
（1）的特解，将它代入所给的差分方程得

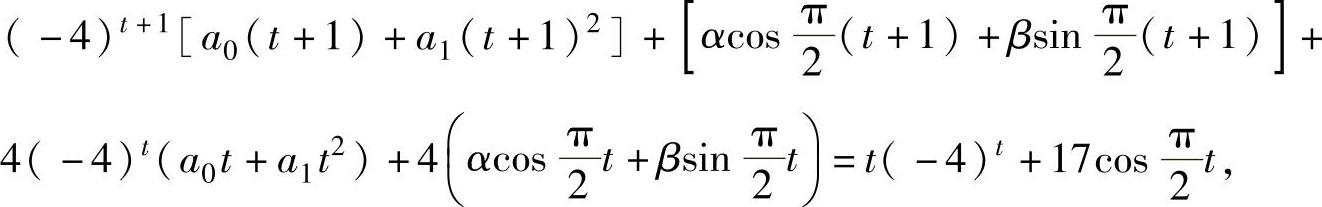
比较上式两边t的同次幂的系数及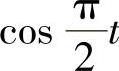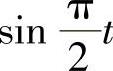，的系数得

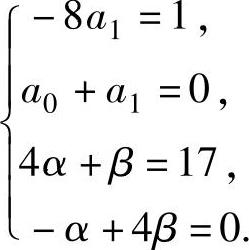
解此方程组得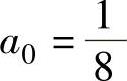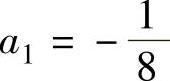，，α=4，β=1.将它代入式（1）得

因此，所给差分方程的通解为

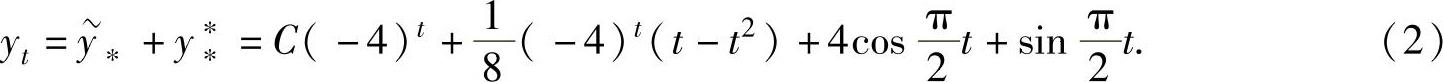
在式（2）中令t=0，并将y₀=1代入得1=C+4，即C=-3.

于是所求的特解为