高阶导数的计算

十一 、高阶导数的计算

【主要内容】

1.高阶导数的概念

这里仅叙述二阶导数的定义，三阶、四阶、…、n阶导数同样可以定义.

如果函数f（x）的导函数f′（x）在点x₀处可导，则称f（x）在点x₀处二阶可导，且称f′（x）在点x₀处的导数为f（x）在点x₀处的二阶导数，记为f″（x₀）或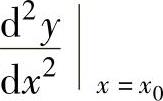，即f″（x₀）=[f′（x）]′_x=x₀ 或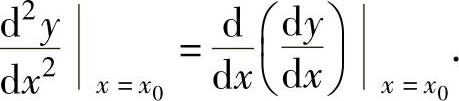

如果函数f（x）在（a，b）的每一点x处都二阶可导，即f″（x）存在，则称f（x）在（a，b）内二阶可导；如果函数f（x）在（a，b）内二阶可导，且f′（x）在点x=a处的右导数和在点x=b处的左导数都存在，则称f（x）在[a，b]上二阶可导（注意此时，f″（a），f″（b）分别为f′（x）在点x=a处的右导数和在点x=b处的左导数）.

2.n阶导数的运算法则

设函数u（x），v（x）都n阶可导，则

[u（x）±v（x）]（n）=u（n）（x）±v（n）（x），

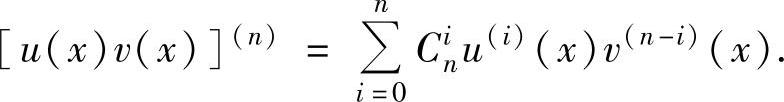
3.常用函数的n阶导数公式，，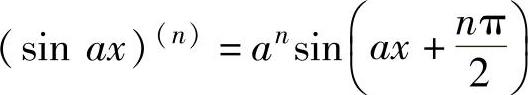

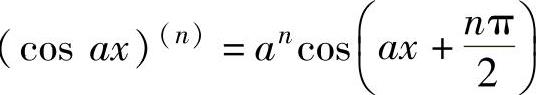（a^x）（n）=axlnna（a>0，且a≠1），特别地，（e^x）（n）=e^x，，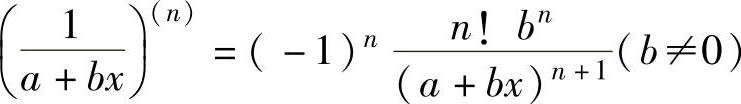

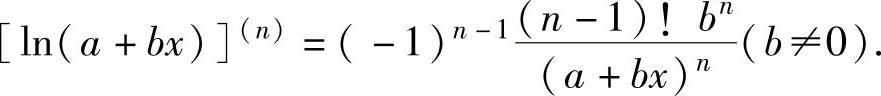
【典型例题】

例1.11.1 设函数f（x）=x³sinx，求f （10）（x）.

精解 由于（x³）′=3x²，（x³）″=6x，（x³）‴=6，（x³）（n）=0（n≥4），所以f （10）（x）=（x³sinx）（10）

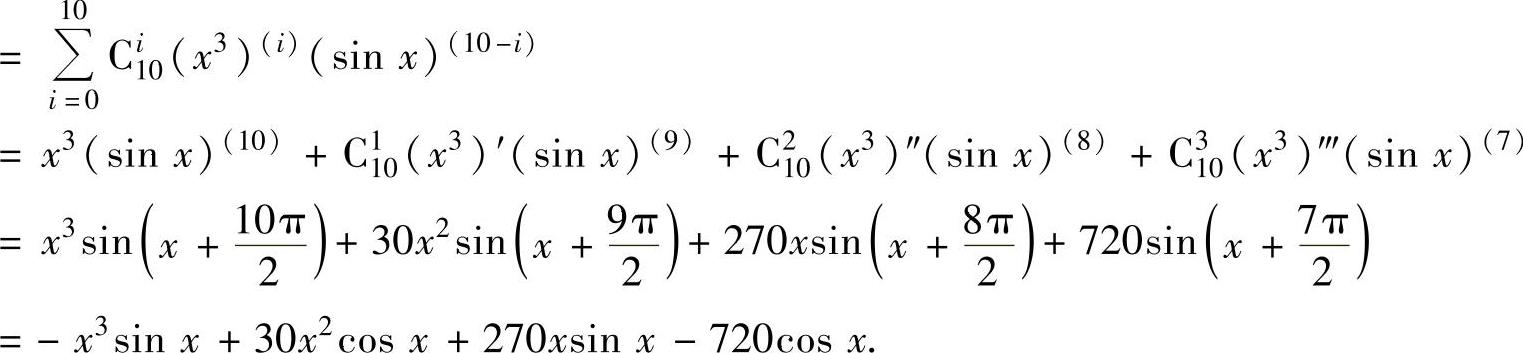
例1.11.2 （单项选择题）已知函数f（x）具有任意阶导数，且f′（x）=[f（x）]²，则当n为大于2的整数时，f（x）的n阶导数f（n）（x）是（）.

A.n！[f（x）]ⁿ⁺¹ B.n[f（x）]ⁿ⁺¹ C.[f（x）]²ⁿ D.n！[f（x）]²ⁿ

精解 计算f′（x），f″（x），f（3）（x），…，根据它们的规律得到f（n）（x）.

由于 f′（x）=[f（x）]²=1！[f（x）]²，

f″（x）={[f（x）]²}′=2f（x）f′（x）=2f（x）[f（x）]²=2！[f（x）]³，

f‴（x）={2！[f（x）]³}′=3！[f（x）]²[f（x）]²=3！[f（x）]⁴，所以，依次类推得

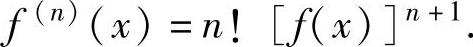
因此本题选A.

例1.11.3 设函数y=y（x）由方程2y-x=（x-y）ln（x-y）确定，求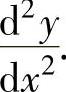

精解 先由隐函数求导方法算出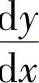，然后计算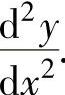

所给方程两边对x求导得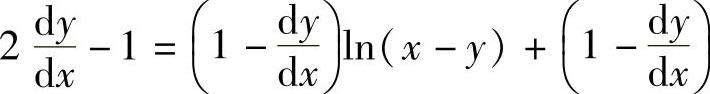，(https://www.daowen.com)

所以，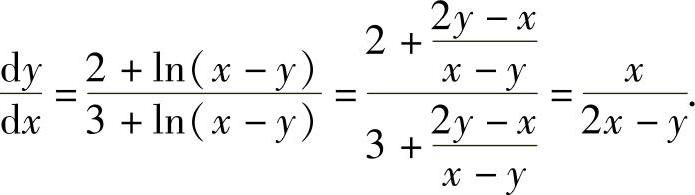

于是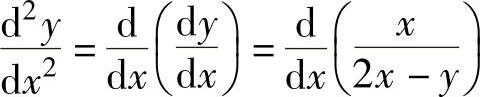

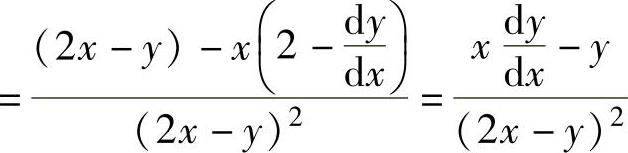
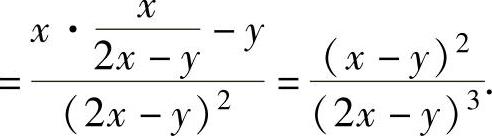
例1.11.4 设函数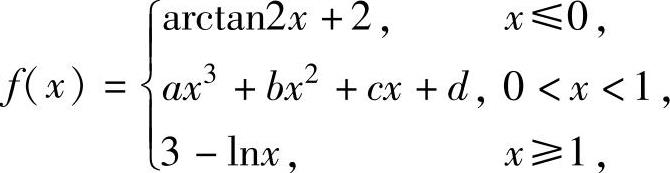

（1）求使f（x）在点x=0，1处都可导的常数a，b，c，d；

（2）由（1）求得的a，b，c，d，求f″（x）.

精解 （1）利用f（x）应在点x=0，1处都连续、可导列出关于a，b，c，d的方程组并解之，即可得到a，b，c，d的值，具体解答如下.

使f（x）在点x=0，1处可导，则a，b，c，d必须满足

即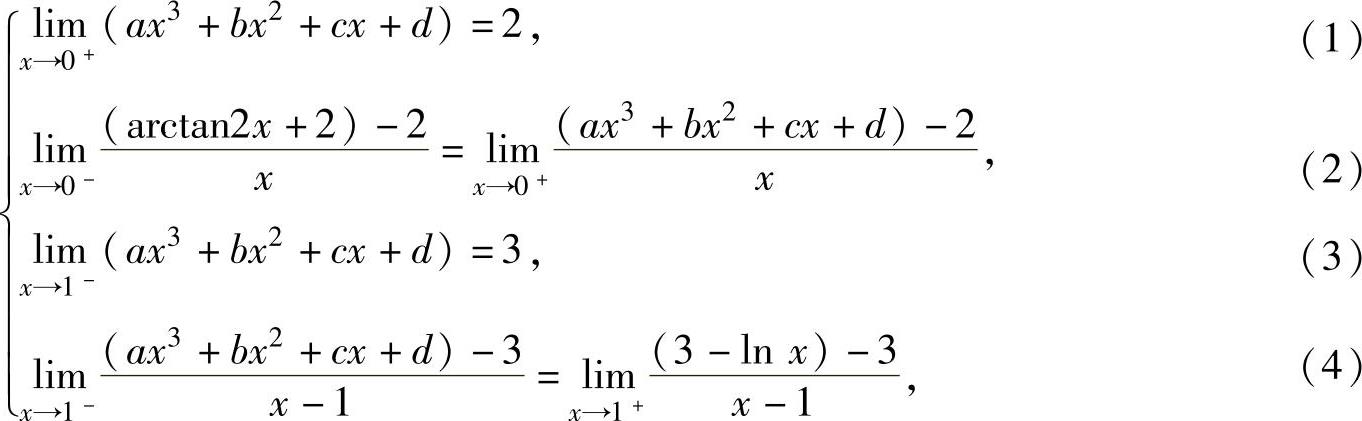

由式（1）得d=2，将它代入式（2）得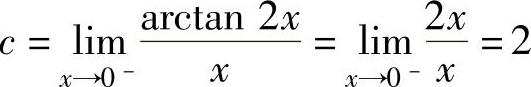，将c=d=2代入式（3）得

b=-1-a，（5）将c=d=2代入式（4）得

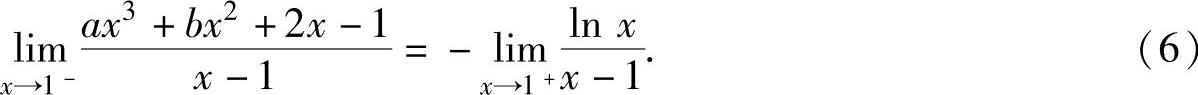
由于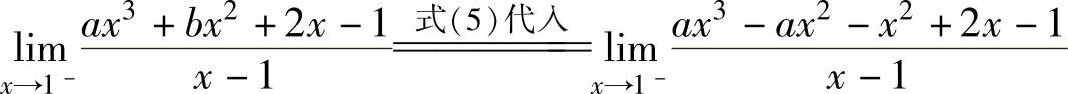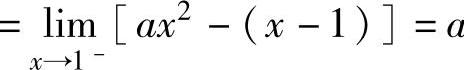a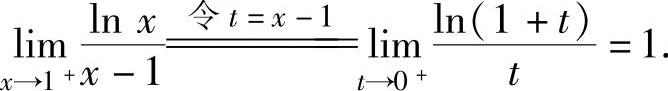，于是将它们代入式（6）得a=-1，代入式（5）得b=0.因此

a=-1，b=0，c=2，d=2.

（2）将（1）计算得到的a，b，c，d的值代入f（x）得

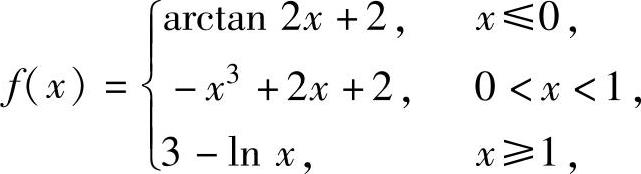
它是可导函数，所以有

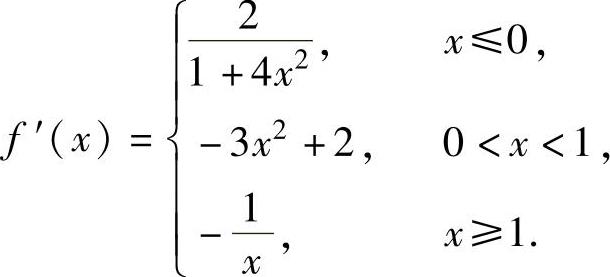
由此可知，x<0时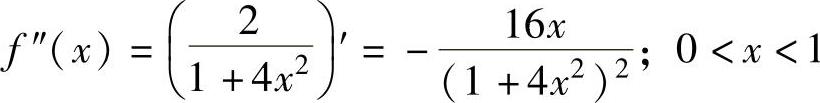，时，f″（x）=（-3x²+

2）′=-6x；x>1时，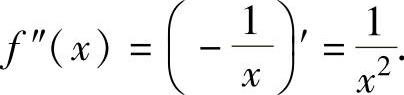

此外，由，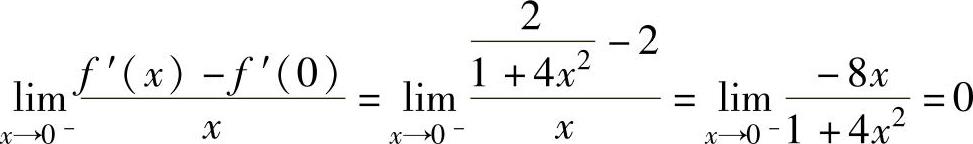

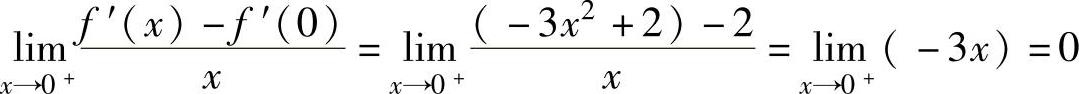
知，f″（0）=0；

由，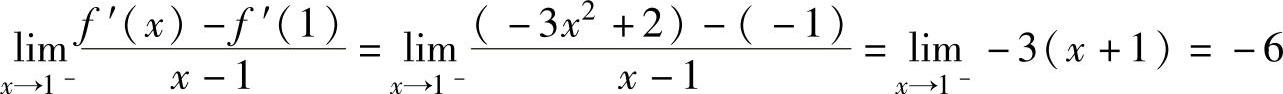

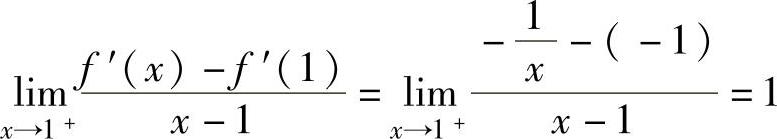
知，f″（1）不存在.因此