正项级数的比值判别法与根值判别法
2026年01月14日
九
、正项级数的比值判别法与根值判别法
【主要内容】
1.正项级数收敛的充分必要条件
如果un≥0(n=1,2,…),则称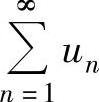 为正项级数.
为正项级数.
正项级数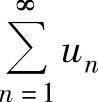 收敛的充分必要条件是它的部分和数列{sn}有上界
收敛的充分必要条件是它的部分和数列{sn}有上界
2.比值判别法
设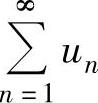 是正项级数.如果
是正项级数.如果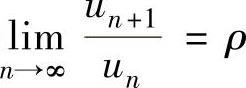 ,则
,则
当ρ<1时,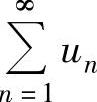 收敛;
收敛;
当ρ>1时,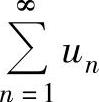 发散;
发散;
当ρ=1时,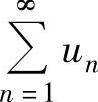 的收敛性要用其他方法判别.
的收敛性要用其他方法判别.
注 当un包含有n!之类的因子,或关于n的若干个因子连乘形式时,往往用比值判别法
判别正项级数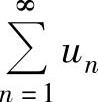 的收敛性.
的收敛性.
3.根值判别法
设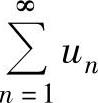 是正项级数,如果
是正项级数,如果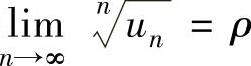 ,则
,则
当ρ<1时,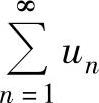 收敛;
收敛;
当ρ>1时,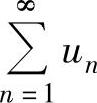 发散;
发散;
当ρ=1时,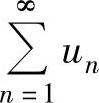 的收敛性要用其他方法判别.
的收敛性要用其他方法判别.
注 当un包含有n或关于n的函数为指数的因子时,往往用根值判别法判别正项级数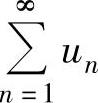 的收敛性.
的收敛性.
【典型例题】
例4.9.1 判别正项级数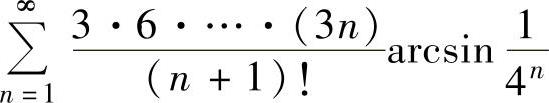 的收敛性.
的收敛性.
精解 用比值判别法判别.记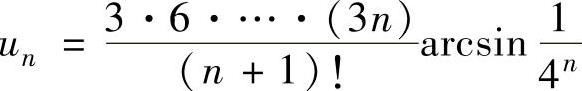 ,则
,则

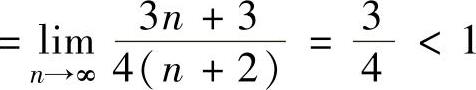 ,
,
所以,所给正项级数收敛.
例4.9.2讨论正项级数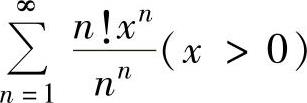 的收敛性与x取值的关系.(https://www.daowen.com)
的收敛性与x取值的关系.(https://www.daowen.com)
精解 用比值判别法进行讨论.记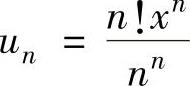 ,则
,则
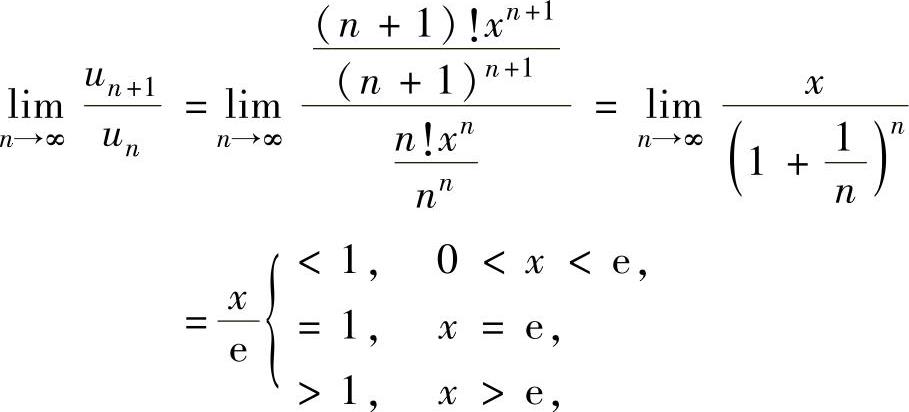
所以由比值判别法知,当0<x<e时,所给正项级数收敛;当x>e时,所给正项级数发散;
当x=e时,由于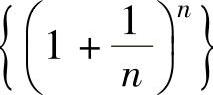 单调增加收敛于e,所以
单调增加收敛于e,所以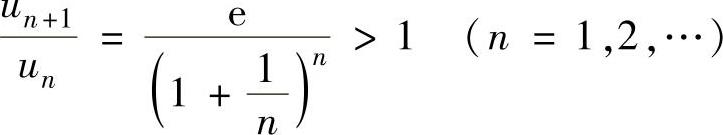 ,
,
即{un}单调增加,于是由un>u1=e(n=2,3,…)知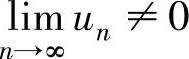 ,由此推出x=e时所给正项
,由此推出x=e时所给正项
级数发散.
例4.9.3 判别正项级数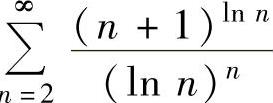 的收敛性.
的收敛性.
精解 用根值判别法判别收敛性.记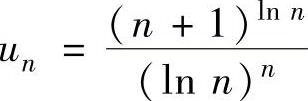 ,则
,则
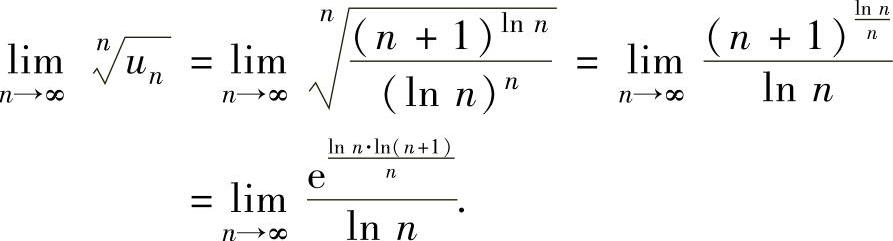
由于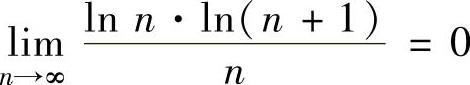 ,所以
,所以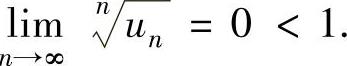 从而所给正项级数收敛.
从而所给正项级数收敛.
例4.9.4 判别正项级数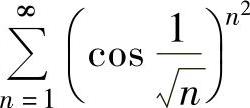 的收敛性.
的收敛性.
精解 用根值判别法判别收敛性.记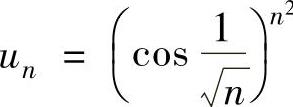 ,则
,则
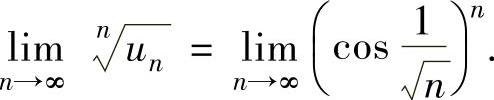
考虑函数极限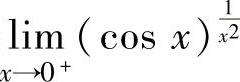 (即将
(即将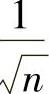 看成x):
看成x):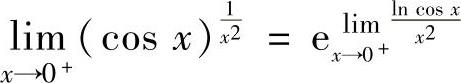 ,(1)
,(1)
其中,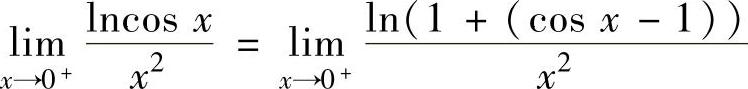
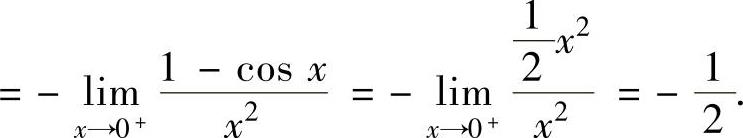
将它代入式(1)得
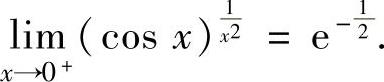
从而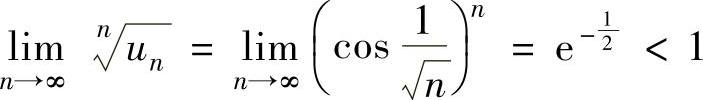 ,因此所给正项级数收敛.
,因此所给正项级数收敛.
例4.9.5 设正项数列{an}单调增加且有上界,证明:级数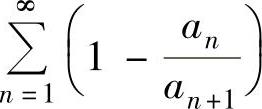 收敛.
收敛.
精解 由{an}单调增加知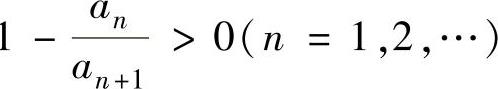 ,因此
,因此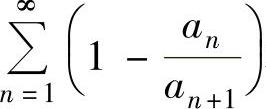 是正项级数,
是正项级数,
于是只要证明数列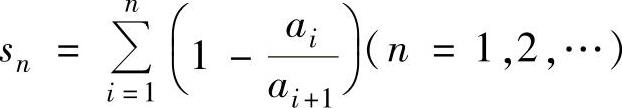 有上界即可.
有上界即可.
记数列{an}的上界为M,则
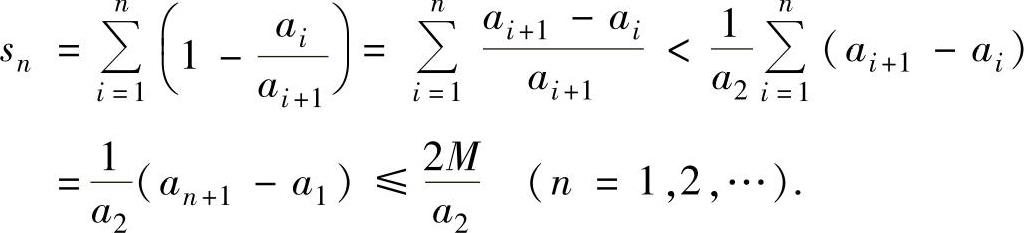
因此,级数
n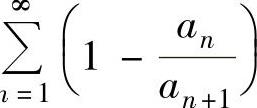 收敛.
收敛.
