练习题三
1.单项选择题
(1)设函数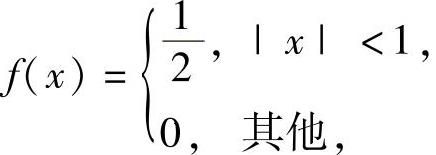 则( ).
则( ).
A.
B.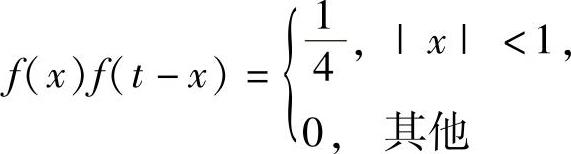
C.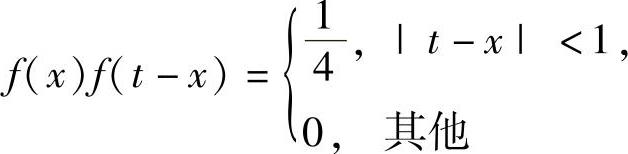
D.
(2)设二元函数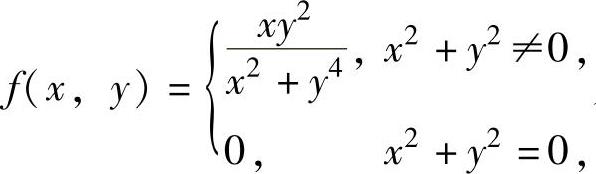 则( ).
则( ).
A.f(x,y)在点(0,0)处连续 B.f(x,y)在点(0,0)处可微
C.fx(0,0)和fy(0,0)都存在 D.fx(x,y)和fy(x,y)在点(0,0)处都连续
(3)设二元函数f(x,y)在点(x0,y0)处的4个二阶偏导数存在,则( ).
A.fyx(x0,y0)=fxy(x0,y0) B.fx(x,y)在点(x0,y0)处可微
C.fx(x,y)在点(x0,y0)处连续 D.fx(x,y0)在点x0处可微
(4)设二元函数u=u(x,y)可微,且当y=x2时,u(x,y)=1及 ,则当y=x2
,则当y=x2
(x≠0)时,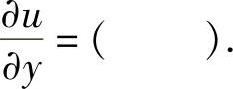
A.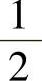 B.
B.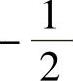 C.0 D.1
C.0 D.1
(5)二元函数z=f(x,y)在点(x0,y0)处可微的充分必要条件为( ).
A.f(x,y)在点(x0,y0)处连续
B.fx(x0,y0)和fy(x0,y0)都存在
C.Δz(x0,y0)=AΔx+BΔy+o(ρ),其中A,B都与Δx,Δy无关,o(ρ)是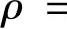
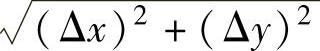 的高阶无穷小
的高阶无穷小
D.fx(x,y)和fy(x,y)都在点(x0,y0)处连续
(6)设二元函数f(x,y)在点(x0,y0)的某个邻域内具有一阶和二阶连续偏导数,且fx(x0,y0)=fy(x0,y0)=0,则下列说法中不正确的是( ).
A.当A>0,AC-B2>0时,f(x0,y0)是极小值
B.当C>0,AC-B2>0时,f(x0,y0)是极小值
C.当AC-B2=0时,f(x0,y0)不是极值
D.当AC-B2<0时,f(x0,y0)不是极值
(7)设二元函数f(x,y)在点(0,0)的某个邻域内连续,且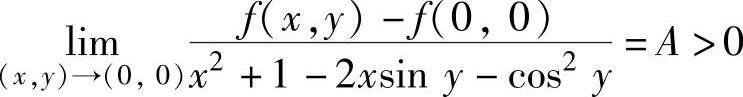 ,则f(0,0)( ).
,则f(0,0)( ).
A.不是极值 B.不能判定是否为极值
C.是极大值 D.是极小值
(8)设二元函数f(x,y)在有界闭区域D上连续,则以下说法正确的是().
A.当(x0,y0)是f(x,y)在D的内部的极大值点时,f(x0,y0)就是f(x,y)在D上的最大值
B.当(x0,y0)是f(x,y)在D的内部的唯一极大值点时,f(x0,y0)就是f(x,y)在D上的最大值
C.当f(x,y)的最大值在D的内部取到,且(x0,y0)是f(x,y)在D的内部的唯一极大值点时,f(x0,y0)就是f(x,y)在D上的最大值
D.当已知f(x,y)的最大值在D的内部取到,且(x0,y0)是f(x,y)在D的内部唯一驻点时,f(x0,y0)就是f(x,y)在D上的最大值
(9)设z=z(x,y),y=y(x,z)都是由方程F(x,y,z)=0确定的二元函数.如果z0=z(x0,y0)是z=z(x,y)的一个极小值,则( ).
A.y0=y(x0,z0)是y=y(x,z)的一个极大值
B.y0=y(x0,z0)是y=y(x,z)的一个极小值
C.y0=y(x0,z0)可能是y=y(x,z)的一个极值
D.y0=y(x0,z0)不是y=y(x,z)的极值
(10)设f(u)是连续函数,D是由曲线y=x2,直线x=-1,x=1及x轴围成的闭区域,
D1是D的第一象限部分,则二重积分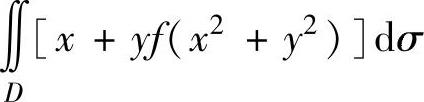 为( ).
为( ).
A.0 B.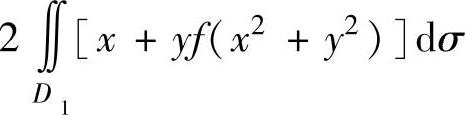 (https://www.daowen.com)
(https://www.daowen.com)
C.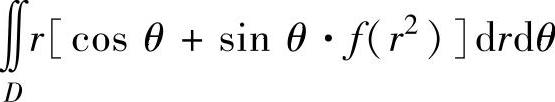 D.
D.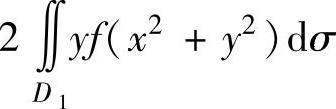
(11)设D是xOy平面上以A(1,1),B(-1,1)和C(-1,-1)为顶点的三角形,D1是
D的第一象限部分,则二重积分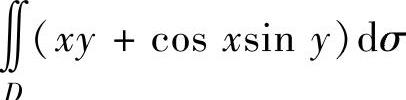 为( ).
为( ).
A.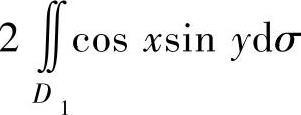 B.
B.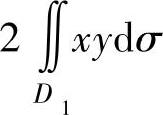
C.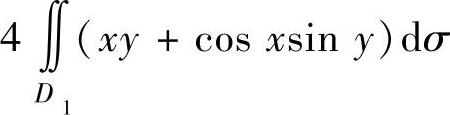 D.0
D.0
(12)设D={(x,y)(x-2)2+(y-1)2≤1},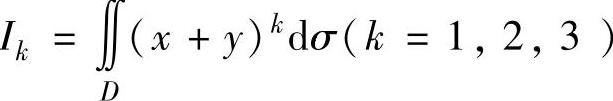 ,比
,比
较I1,I2,I3的大小得( ).
A.I1<I2<I3 B.I2<I1<I3
C.I2<I3<I1 D.I3<I2<I1
(13)设f(x,y)是连续函数,则二次积分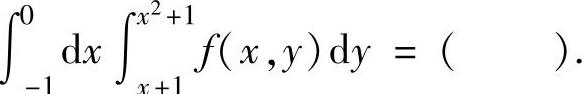
A.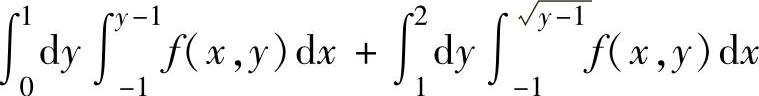
B.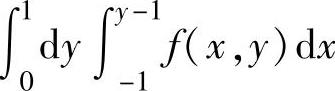
C.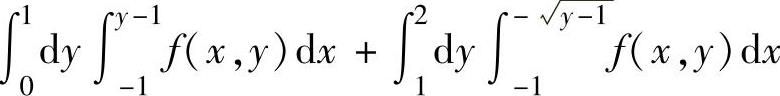
D.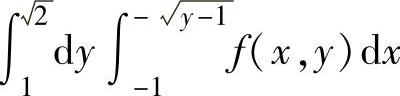
(14)二次积分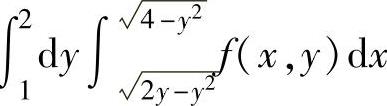 (其中,f(x,y)是连续函数)的极坐标表示为( ).
(其中,f(x,y)是连续函数)的极坐标表示为( ).
A.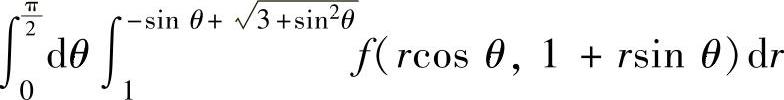
B.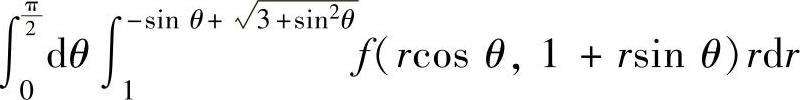
C.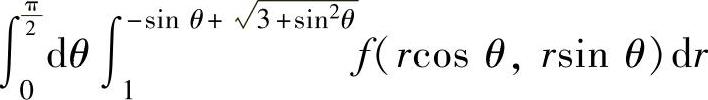
D.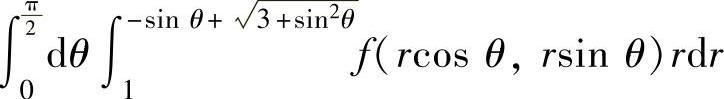
2.解答题
(1)设二元函数f(x,y)在点(1,1)处可微,且f(1,1)=1,fx′(1,1)=2,fy′(1,1)=3,φ(x)=f(x2,f(x2,x)),求φ′(x),φ′(1).
(2)设二元函数z=z(x,y)由方程z-x-y+xyez-x=0确定,求dz.
(3)求二元函数z=xx+y+(x+1)ln(1+y)的两个偏导数.
(4)设二元函数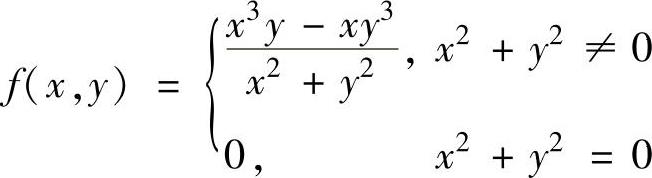 ,求fx′(x,y)及f″xy(0,0).,
,求fx′(x,y)及f″xy(0,0).,
(5)设三元函数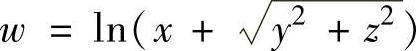 ,求在点A(1,0,1)处沿点A指向点B(3,-2,
,求在点A(1,0,1)处沿点A指向点B(3,-2,
2)的方向导数.
(6)设二元函数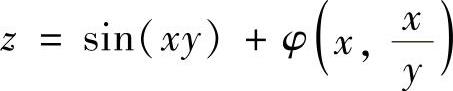 ,其中,φ(u,v)具有二阶偏导数,求z″xy.
,其中,φ(u,v)具有二阶偏导数,求z″xy.
(7)设二元函数f(u,v)由关系式f(xg(y),y)=x+g(y)确定,其中函数g(y)可微,且g(y)≠0,求f″uv.
(8)求二元函数f(x,y)=xyln(x2+y2)的极值.
(9)求三元函数w=sinxsinysinz(x>0,y>0,z>0)在约束条件 下的最值.
下的最值.
(10)求三元函数w=xyz在约束条件x2+y2+z2=1及x+y+z=0下的最大值与最小值.
(11)求二元函数z=x2+y2在圆域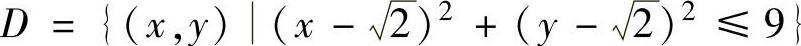 上的最
上的最
大值与最小值.
(12)求二次积分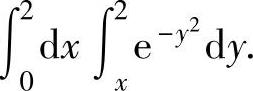
(13)设D={(x,y)|x2+y2≤1},求二重积分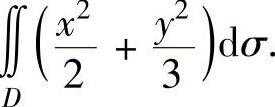
(14)设二元函数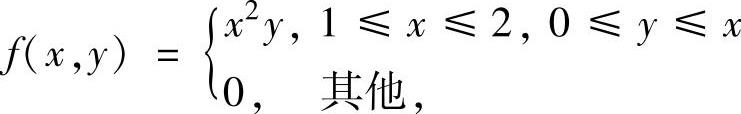 ,D={(x,y)|x2+y2≥2x},
,D={(x,y)|x2+y2≥2x},
求二重积分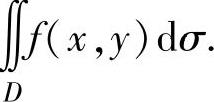
(15)设D={(x,y)|0≤x≤1,0≤y≤1},求二重积分∬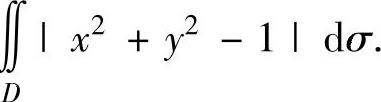
(16)求二重积分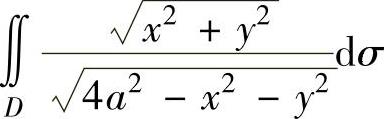 ,其中D是由曲线
,其中D是由曲线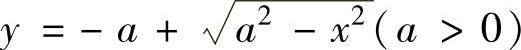 和
和
直线y=-x围成的平面区域.
