函数的单调性
【主要内容】
设f′（x）>0（x∈（a，b））或f′（x）≥0（x∈（a，b），但仅在有限个点处取等号），则函数f（x）在（a，b）内单调增加；设f′（x）<0（x∈（a，b））或f′（x）≤0（x∈（a，b），但仅在有限个点处取等号），则函数f（x）在（a，b）内单调减少.
注 （ⅰ）以上结论在a=-∞或b=+∞时仍成立；
（ⅱ）当f（x）在[a，b]上连续时，端点x=a，x=b可以并入到f（x）的单调区间中去.
【典型例题】
例1.17.1 计算下列函数的单调区间：
（1）
；
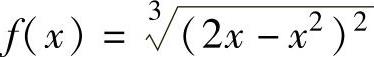（2）
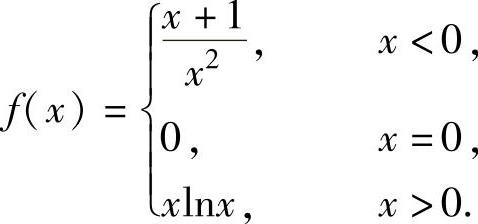
精解 （1）f（x）的定义域为（-∞，+∞），且在定义域上连续，由
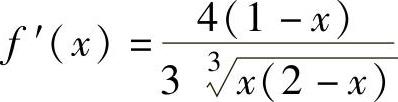
可知，f（x）的驻点（即使f′（x）=0的点）为x=1，不可导点为x=0，2.据此列表如下：
由表可知，f（x）的单调增加区间为[0，1]和[2，+∞），单调减少区间为（-∞，0]和[1，2].
（2）当x<0时，由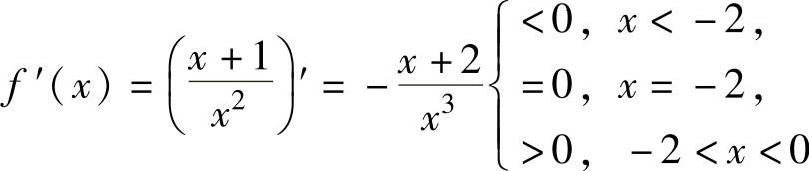
知f（x）在（-∞，-2]上
单调减少，在[-2，0）上单调递增.
知f（x）在0，1
[e]上单调减少（这里由于
f（x）在点x=0处右连续），在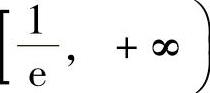
上单调递增.
因此，f（x）的单调增加区间为[-2，0）和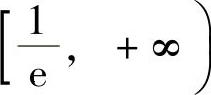
，单调减少区间为（-∞，-2]和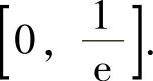
例1.17.2 设函数在（-∞，+∞）上二阶可导，且f（0）=0，f″（x）>0.证明：
（-∞，0）和（0，+∞）都是函数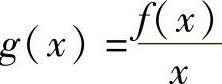
的单调增加区间.
精解 当x≠0时，g（x）可导且
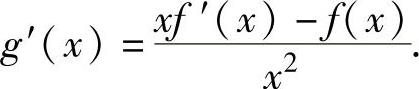
为了判定g′（x）的正负性，记φ（x）=xf′（x）-f（x），则φ（x）在（-∞，+∞）上可导且
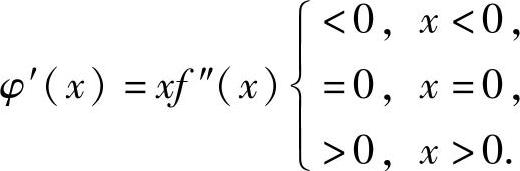
所以，当x≠0时，φ（x）>φ（0）=0（这是因为，当x<0时，φ（x）单调减少，从而有φ（x）>φ（0）；当x>0时，φ（x）单调增加，从而有φ（x）>φ（0）），因此g′（x）>0.由此得到（-∞，0）和（0，+∞）都是函数g（x）的单调增加区间.
例1.17.3 问常数a（a>0）为何值时，函数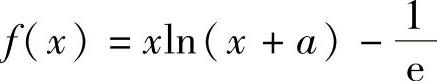
仅有单调减少区间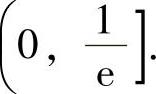
精解 利用f′（x）算出f（x）的单调减少区间，将它与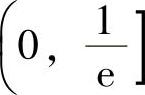
比较即可确定a的值.
f（x）的定义域为（-a，+∞），在其上f（x）二阶可导且有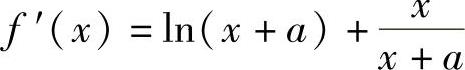
，
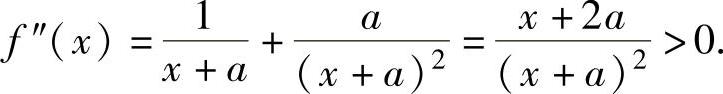
所以，f′（x）在（-a，+∞）上单调增加，此外，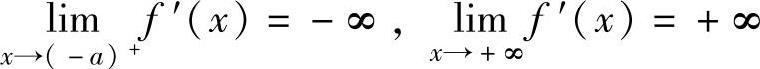
，
所以，方程f′（x）=0在（-a，+∞）上有且仅有一个实根，记为x0，则
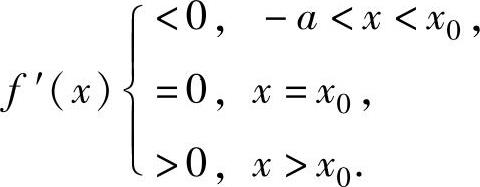
由此可知，f（x）的单调减少区间为（-a，x0].将它与题设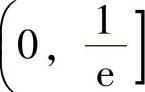
比较，得a=0（且容
易检验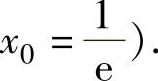
注 设函数φ（x）在[a，b]上连续时，如果f（a）f（b）<0，且f（x）在（a，b）内单调增加（或单调减少），则方程φ（x）=0在（a，b）内有唯一实根.
上述结论有各种推广形式，例如：当函数f（x）在（a，+∞）上连续时，如果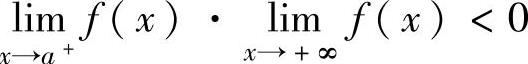
，且f（x）在（a，+∞）上单调增加（或单调减少），则方程f（x）=0在（a，+∞）上有唯一实根.
本题解答中应用了上述的推广形式.应记住这个结论及其推广形式.
例1.17.4 （单项选择题）设函数f（x）在定义域内可导，且y=f（x）的图形如图1.17.4所示，则导函数y=f′（x）的图形为（）.
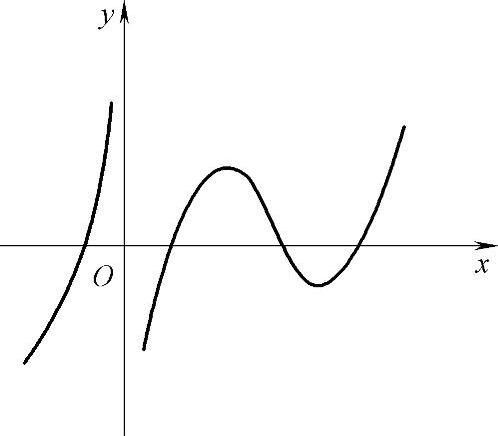
图 1.17.4
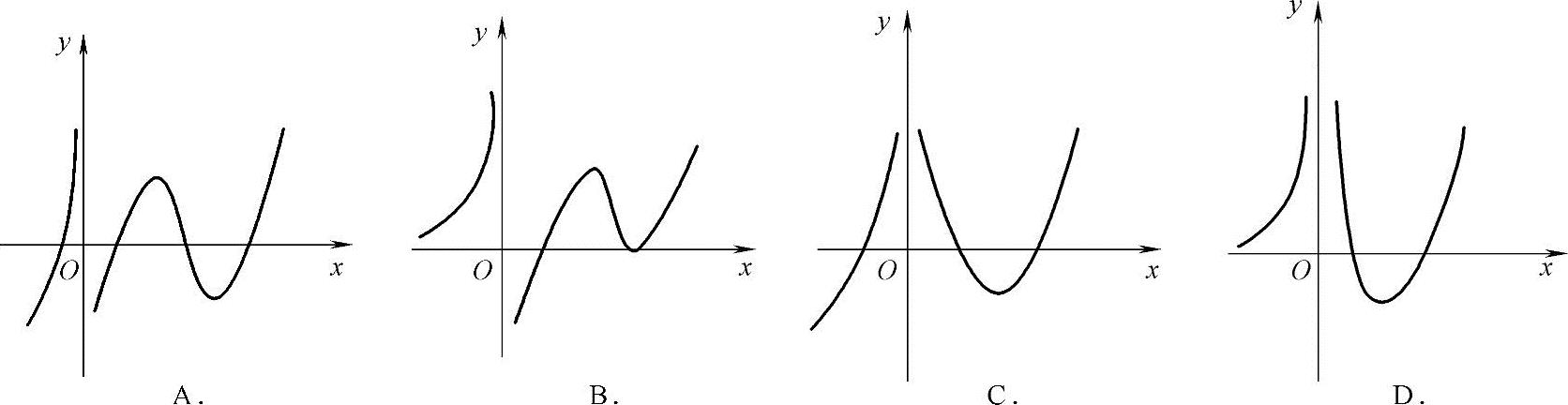
精解 由y=f（x）的图形可知，当x<0时，f（x）单调增加，f′（x）不能取负值，于是选项A、C不能选.
当x>0时，曲线y=f（x）靠近y轴部分单调增加，所以当x较小时f′（x）不会取负值.于是选项B不能选.
因此本题选D.