随机变量的方差与矩

十七 、随机变量的方差与矩

【主要内容】

1.随机变量方差的定义与性质

设X是随机变量，如果E（X-EX）2存在，则称DX=E（X-EX）2为X的方差，称D（X）为X的标准差.方差有以下性质.

（1）Dc=0（其中，c是常数）；

（2）D（cX）=c²DX，D（X+c）=DX（其中，c是常数）；

（3）设随机变量X₁与X₂相互独立，则

D（c₁X₁+c₂X₂）=c²₁DX₁+c²₂DX₂（其中，c₁，c₂是常数）；

（4）DX=EX²-（EX）2.

注 方差DX可以用定义计算，但在许多场合下是按公式DX=EX²-（EX）2计算.此外利用这个公式也可以计算EX²，即EX²=DX+（EX）2.

2.常用随机变量的方差

设X服从0-1分布，则DX=p（1-p）.

设X～B（n，p），则DX=np（1-p）.

设X～π（λ），则DX=λ.

设X～U[a，b]，则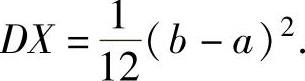

设X～E（λ），则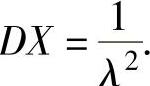

设X～N（μ，σ²），则DX=σ².

3.随机变量矩

设X是随机变量.如果EX^k存在，则称它是X的k阶矩，记为μ_k，即μ_k=EX^k；如果E（X-EX）k存在，则称它是X的k阶中心矩，记为ν_k，其中k=1，2，….

显然_μ1=EX，ν₂=DX.

【典型例题】

例7.17.1 求方差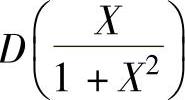，其中随机变量的分布函数为

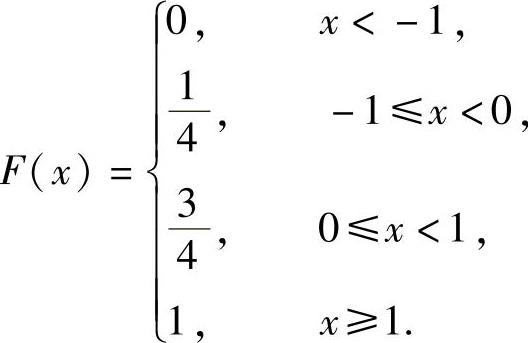
精解 X是离散型随机变量，先算出它的分布律，然后计算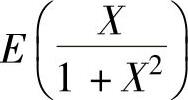和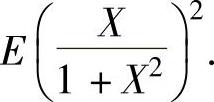

由于F（x）的间断点为x=-1，0，1，所以X的分布律为

即

所以，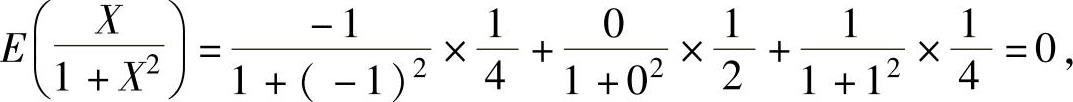

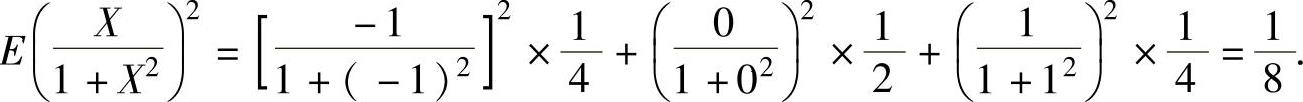
因此，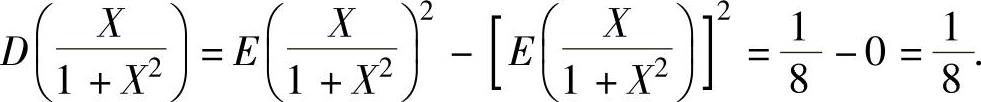

例7.17.2 设随机变量X与Y相互独立，X～E（4），Y～N（2，2），求E（3Y+X²-XY）和D（3Y+X²）.

精解 由随机变量数学期望的性质知(https://www.daowen.com)

E（3Y+X²-XY）=3EY+EX²-E（XY）=3EY+DX+（EX）2-EX·EY，（1）

其中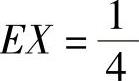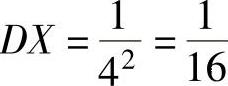，，，EY=2.将它们代入式（1）得

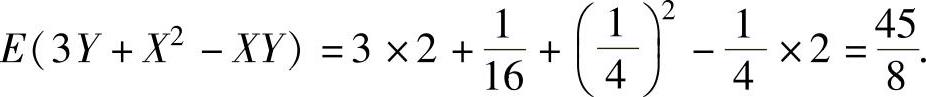
D（3Y+X²）=D（3Y）+DX² （由X与Y相互独立知X²与3Y也相互独立）

=9DY+EX⁴-（EX²）2，

其中，DY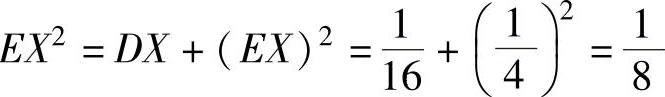=2，，（2）

将它们代入式（2）得

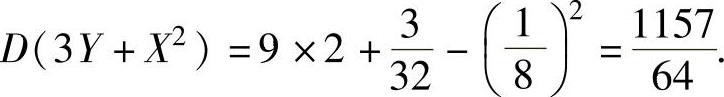
例7.17.3 设随机变量U在[-2，2]上服从均匀分布，记随机变量

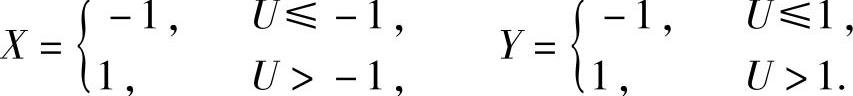
求：（1）二维随机变量（X，Y）的分布律；

（2）方差D（X+Y）.

精解 （1）（X，Y）全部可能取的值为（-1，-1），（-1，1），（1，-1）和（1，1），并且对应的概率为

P（X=-1，Y=1）=P（U≤-1，U>1）=P（ ）=0，

P（X=-1，Y=-1）=P（U≤-1，U≤1）=P（U≤-1）=P（-2≤U≤-1），（1）

由于U在[-2，2]上服从均匀分布，而[-2，-1]的长度是[-2，2]的长度的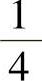，所以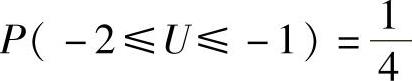，将它代入式（1）得，

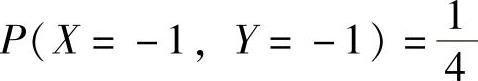同样，，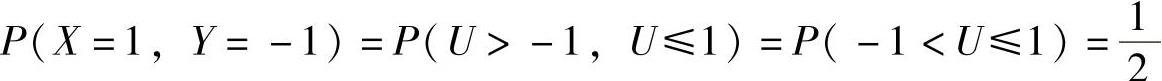

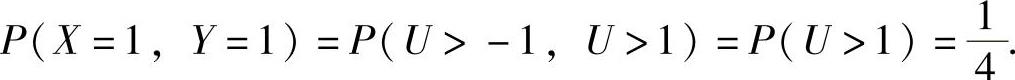
因此（X，Y）的分布律可用表表示为

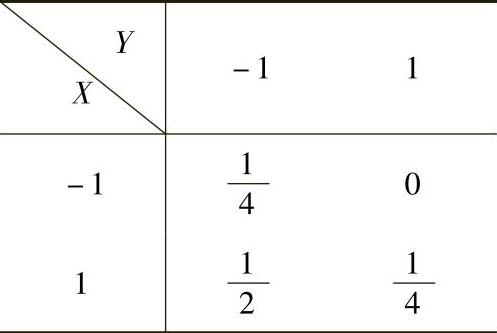
（2）D（X+Y）=E（（X+Y）2）-[E（X+Y）]²，（2）其中，由上述算得的（X，Y）的分布律可得

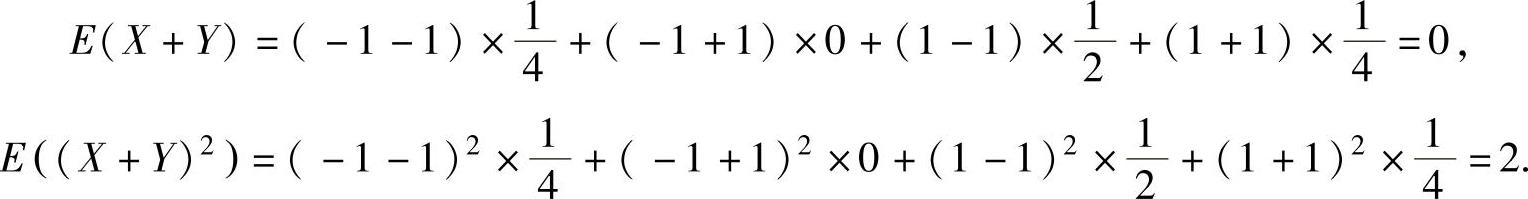
将它们代入式（2）得

D（X+Y）=2-0²=2.

例7.17.4 设随机变量X的概率密度为

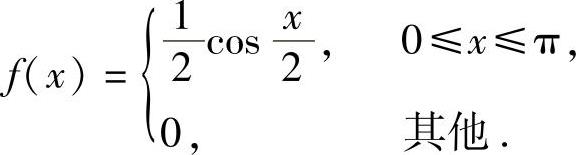
对X独立重复观察4次，用Y表示观察值大于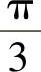的次数，求EY2.

精解 Y～B（4，p），其中，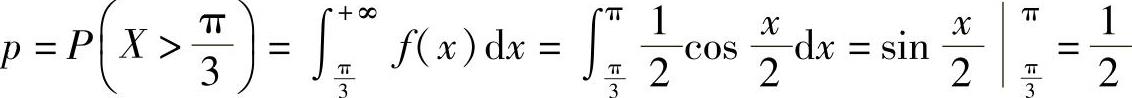

所以