两个随机变量的独立性
【主要内容】
设二维随机变量(X,Y)的分布函数为F(x,y),边缘分布函数为FX(x)和FY(y).如果对任意实数x,y有F(x,y)=FX(x)FY(y),则称X与Y相互独立(简称独立).
当(X,Y)是二维离散型随机变量,其分布律为P(X=xi,Y=yi)=pij(i=1,2,…,m,…;j=1,2,…,n,…),边缘分布律为P(X=xi)=pi·(i=1,2,…,m,…)和P(Y=yj)(j=1,2,…,n,…)时,X与Y相互独立的充分必要条件是对任意i,j都有
pij=pi··p·j
当(X,Y)是二维连续型随机变量,其概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),边缘概率密度为fX(x)(-∞<x<+∞)和fY(y)(-∞<y<+∞)时,X与Y相互独立的充分必要条件是
f(x,y)=fX(x)fY(y)在xOy平面上几乎处处成立.
注 (ⅰ)设随机变量X与Y相互独立,g(x),h(y)是连续函数,则随机变量Z1=g(X)与Z2=h(Y)也相互独立.
(ⅱ)多个随机变量的独立性也可类似定义.
如果对任意实数x1,x2,…,xn有
F(x1,x2,…,xn)=F1(x1)F2(x2)…Fn(xn),则称随机变量X1,X2,…,Xn相互独立,其中F是n维随机变量(X1,X2,…,Xn)的分布函数,F1,F2,…,Fn分别是随机变量X1,X2,…,Xn的分布函数.
【典型例题】
例7.13.1 (单项选择题)设两个随机变量X与Y相互独立,且有相同的分布律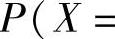
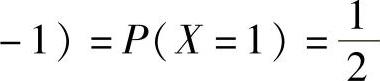 ,则下列等式中成立的是( ).
,则下列等式中成立的是( ).
A.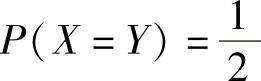 B.P(X=Y)=1C.
B.P(X=Y)=1C.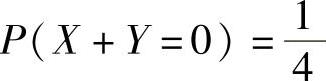 D.
D.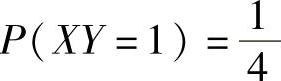
精解 先考虑选项A.
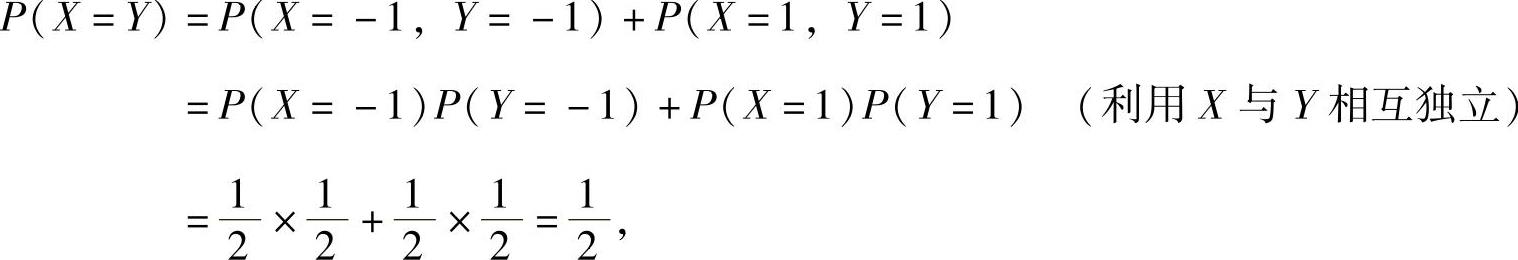
因此本题选A.
例7.13.2 设随机变量X与Y相互独立,二维随机变量(X,Y)的分布律及边缘分布律如下表所示:

求其中用文字表示的各个概率值.
精解 由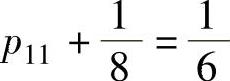 得
得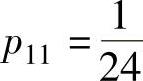 ;由
;由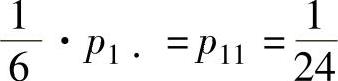 得
得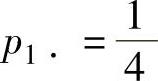 ;
;
由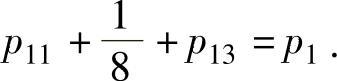 ,即
,即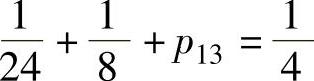 得
得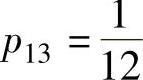 ;
;
由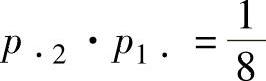 ,即
,即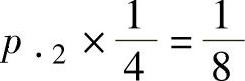 得
得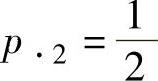 ;
;
由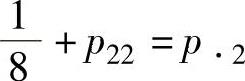 得
得 ;
;
由 p2·p·2=p22,即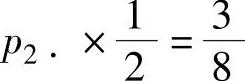 得
得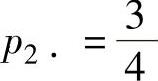 ;
;
由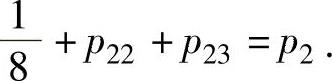 ,即
,即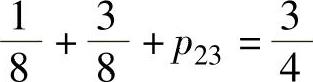 得
得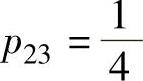 ,
,
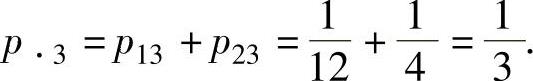
例7.13.3 设随机变量X与Y相互独立,X~E(5),Y~U[0,2],求:
(1)二维随机变量(X,Y)的概率密度f(x,y);
(2)概率P(Y≥X).(https://www.daowen.com)
精解 (1)由题设知,X与Y的概率密度分别为
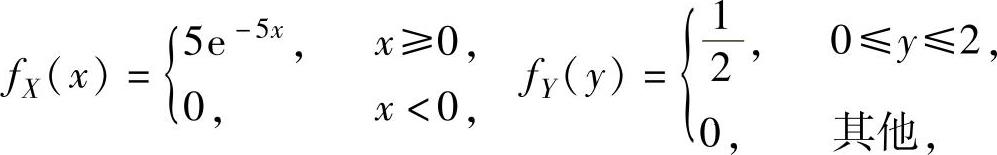
所以,由X与Y相互独立得(X,Y)的概率密度为
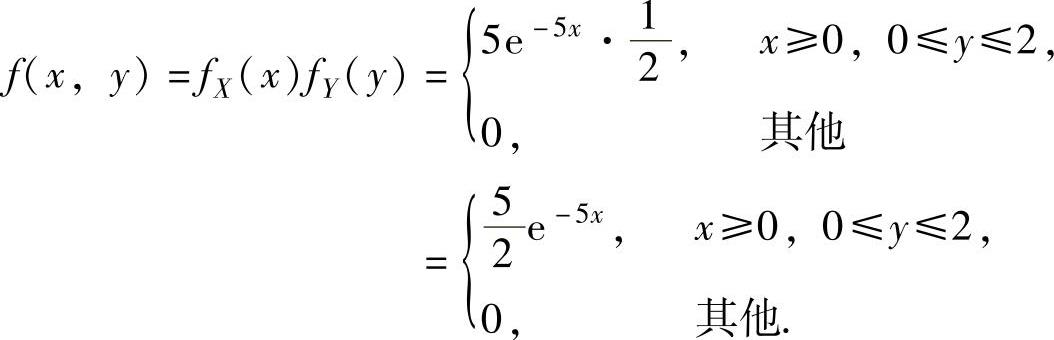
(2)由(1)知,f(x,y)在D={(x,y)x≥0,0≤y≤2}(如图7.13.3阴影部分所示)上取值为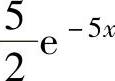 ,在xOy平面的其他部分取值为零.P(Y≥X)=P((X,Y)∈D1)(其中D1={(x,y)y≥x})
,在xOy平面的其他部分取值为零.P(Y≥X)=P((X,Y)∈D1)(其中D1={(x,y)y≥x})
=P((X,Y)∈D∩D1=△OAB)(△OAB如图7.13.3所示)
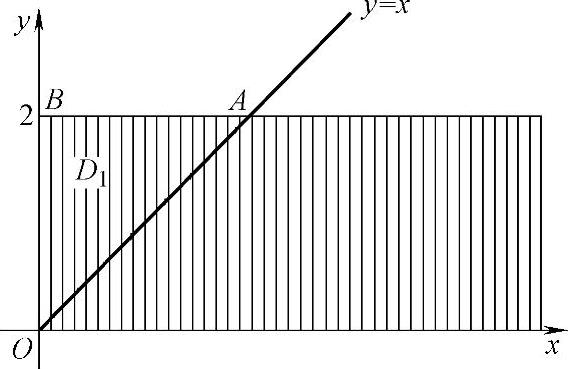
图 7.13.3
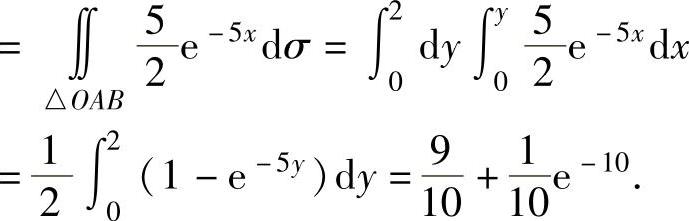
例7.13.4 设随机变量X与Y相互独立,又设随机变量Z在[0,1]上随机取值,当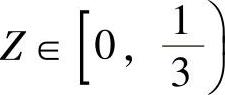 时,X与Y都服从U[0,1];当
时,X与Y都服从U[0,1];当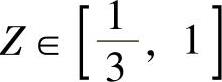 时,X与Y都服从B(2,0.8),求关
时,X与Y都服从B(2,0.8),求关
于t的二次方程t2+Xt+Y=0有实根的概率.
精解 记A={所给二次方程有实根},则

当X,Y都服从U[0,1]时,它们的概率密度分别为
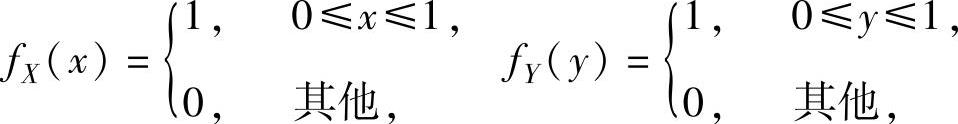
所以,由X与Y相互独立得(X,Y)的概率密度为
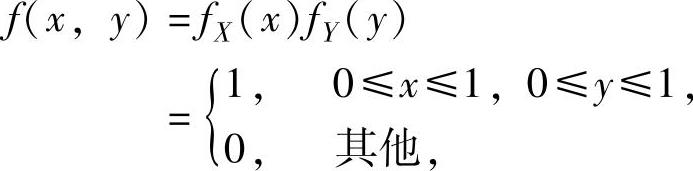
由此得到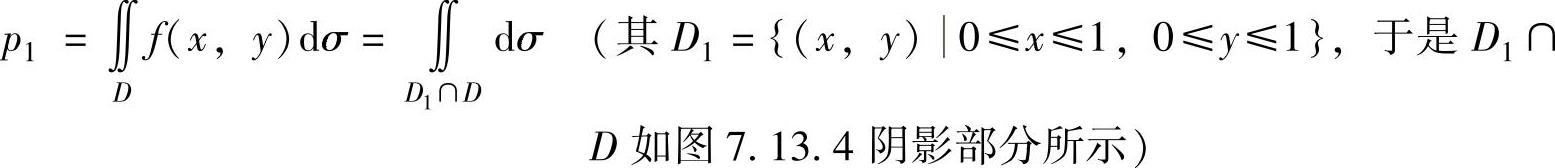

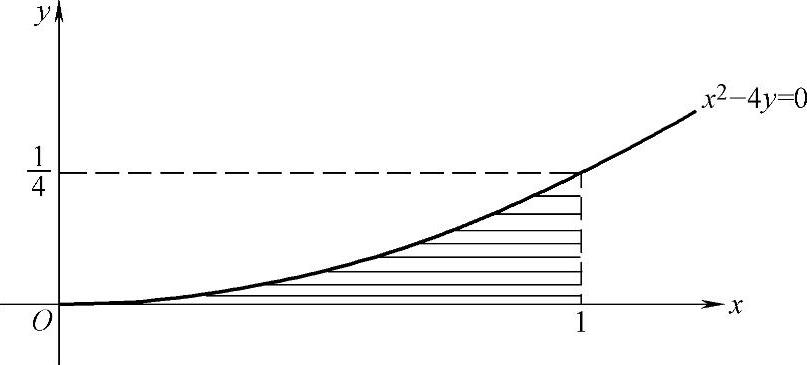
图 7.13.4
当X,Y都服从B(2,0.8)时,它们的分布律分别为
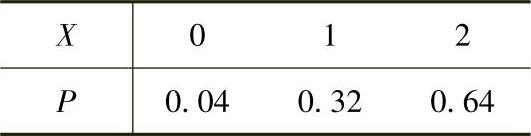
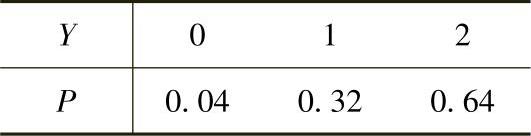
所以,由X与Y相互独立得
p2=P((X,Y)∈D)=P(X=0,Y=0)+P(X=1,Y=0)+P(X=2,Y=0)+P(X=2,Y=1)
=P(X=0)P(Y=0)+P(X=1)P(Y=0)+P(X=2)P(Y=0)+P(X=2)P(Y=1)
=0.04×0.04+0.32×0.04+0.64×0.04+0.64×0.32
=0.2448.(3)
将式(2)、式(3)代入式(1)得