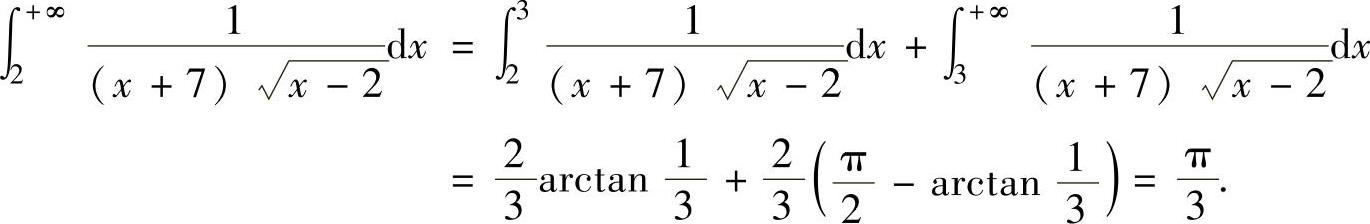反常积分收敛性的概念及其计算
【主要内容】
1.无穷限反常积分
（1）无穷限反常积分定义
设函数f（x）在[a，+∞）上连续.如果极限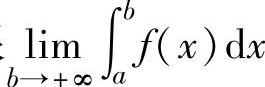
存在，则称这个极限值为f（x）
在[a，+∞）上的反常积分，记为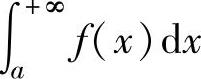
，此时称反常积分
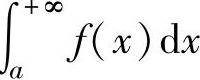收敛；如果极限
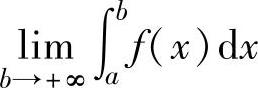不存在，则称反常积分
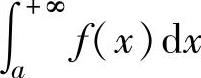发散.
设函数f（x）在（-∞，b]上连续.如果极限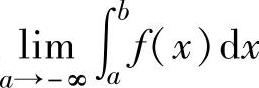
存在，则称这个极限值为f（x）在
（-∞，b]上的反常积分，记为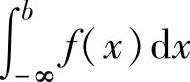
，此时称反常积分
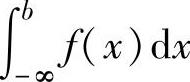收敛；如果极限
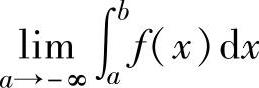不存在，则称反常积分
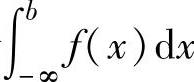发散.
设函数f（x）在（-∞，+∞）上连续.如果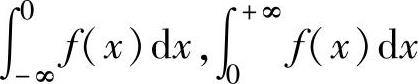
都收敛，则称它们的和
为f（x）在（-∞，+∞）上的反常积分，记为∫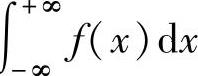
，此时称反常积分∫
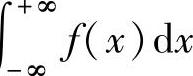收敛；如果
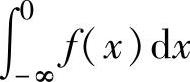和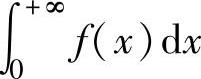
中至少有一个发散，则称反常积分
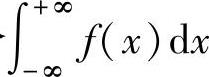发散.
注 （ⅰ）设f（x）是[a，+∞）上的非负连续函数，则当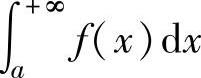
收敛时，其值即为曲线
y=f（x）与x轴之间的位于直线x=a右边的平面图形面积.
（ⅱ）在计算收敛的反常积分时，也有像定积分中牛顿-莱布尼茨公式那样的记法，例如，
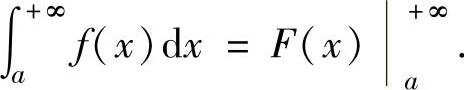
其中，F（x）是f（x）的一个原函数，把+∞代入F（x）应理解为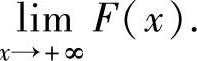
（2）无穷限反常积分收敛性判别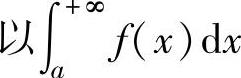
为例.
设函数f（x）在[a，+∞）上连续且f（x）≥0.如果存在常数p>1，使得lim
x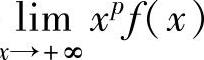
存在，
则反常积分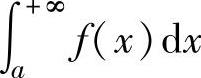
收敛；如果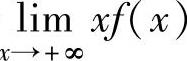
为正数或无穷大，则反常积分
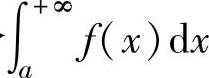发散.
2.无界函数的反常积分
（1）无界函数反常积分的定义
设函数f（x）在（a，b]上连续，且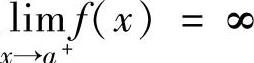
（称x=a为瑕点）.如果极限lim
t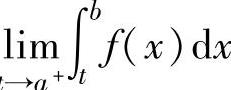
存在，则称这个极限值为f（x）在[a，b]上的反常积分，记为∫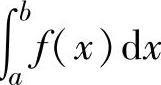
，此时称反常积分
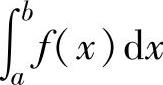收敛；如果极限
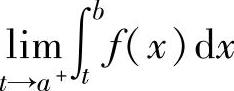不存在，则称反常积分∫
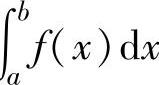发散.
设函数f（x）在[a，b）上连续，且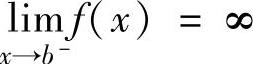
（称x=b为瑕点）.如果极限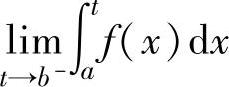
存在，则称这个极限值为f（x）在[a，b]上的反常积分，记为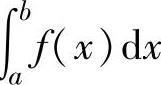
，此时称反常积分
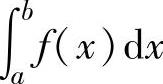收敛；如果极限
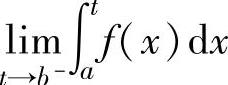不存在，则称反常积分
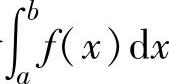发散.
设函数f（x）在[a，b]上除点x=c（a<c<b）外处处连续，且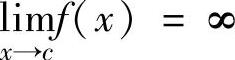
（称x=c为
瑕点）.如果反常积分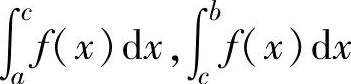
都收敛，则称它们的和为f（x）在[a，b]上的反常积
分，记为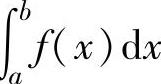
，此时称反常积分
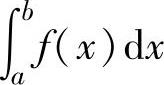收敛；如果
中至少有一个发
散，则称反常积分
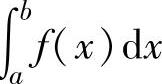发散.
注 在计算收敛的反常积分时，也有像定积分中的牛顿-莱布尼茨公式那样的记法，例如，当x=a为瑕点时，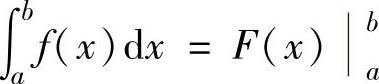
，(https://www.daowen.com)
其中，F（x）是f（x）的一个原函数，将a代入F（x）应理解为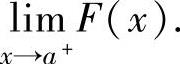
（2）无界函数反常积分收敛性的判别
以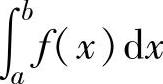
（其中，仅有瑕点x=a）为例.
设函数f（x）在（a，b]上连续，且f（x）≥0，但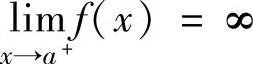
.如果存在常数0<q<1，使
得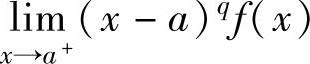
存在，则反常积分∫
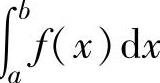收敛；如果
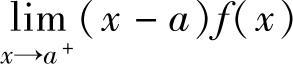为正数或无穷大，则
反常积分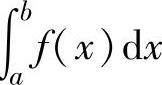
发散.
【典型例题】
例2.11.1 求反常积分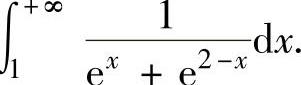
精解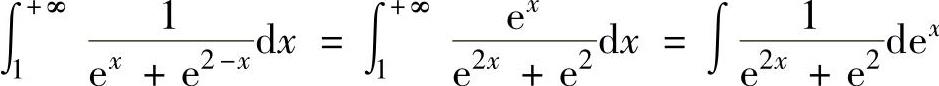
例2.11.2 已知lim
x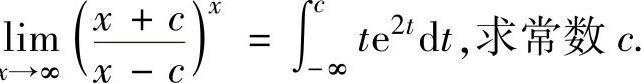
精解 分别求出所给等式左边的极限与右边的反常积分，解由此得到的关于c的方程即可得到c的值.由于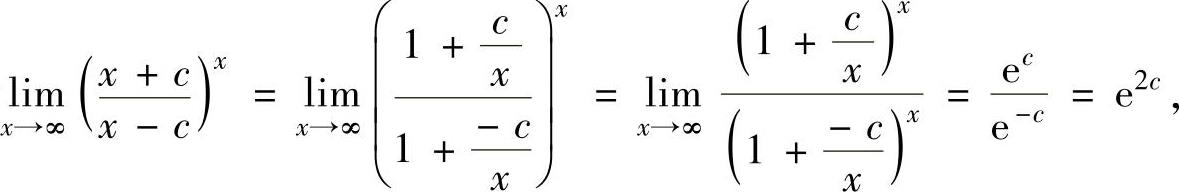
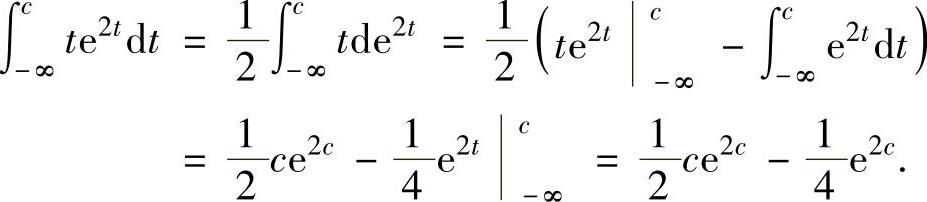
于是题设中所给的等式成为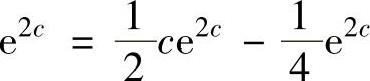
， 即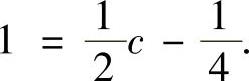
解此方程得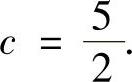
例2.11.3 设f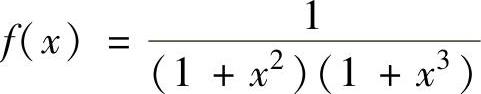
，求在曲线y=f（x）与x轴之间的位于右半平面
的平面图形的面积S.
精解 由于f（x）>0（x∈[0，+∞）），所以
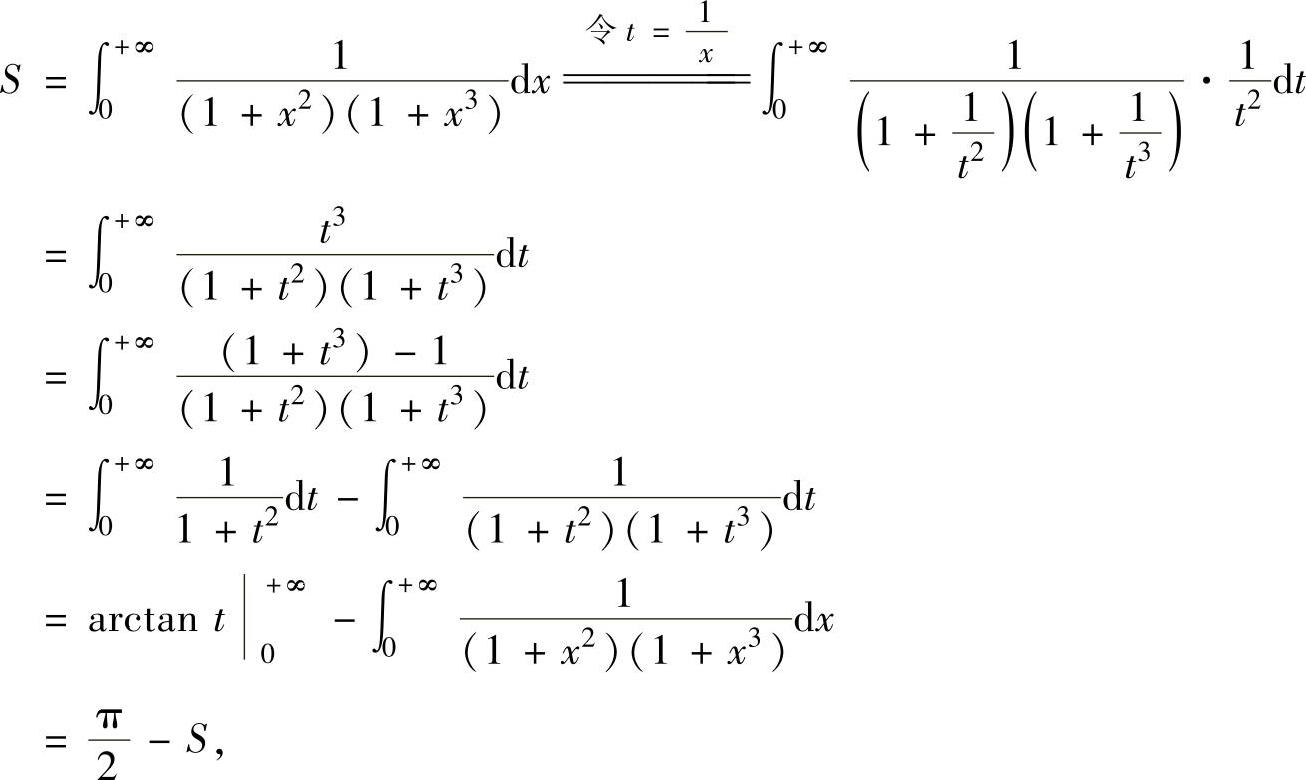
即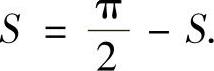
因此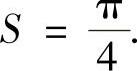
例2.11.4 求反常积分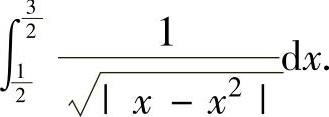
精解 被积函数在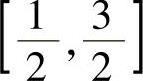
上仅有瑕点x=1，因此分别计算反常积分
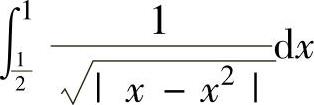和∫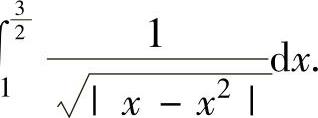
由于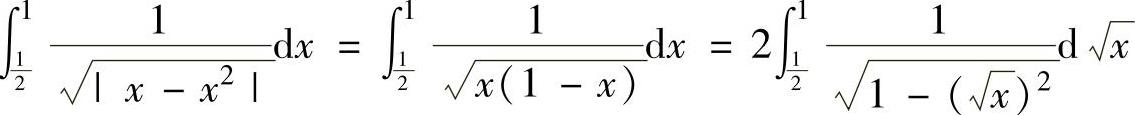
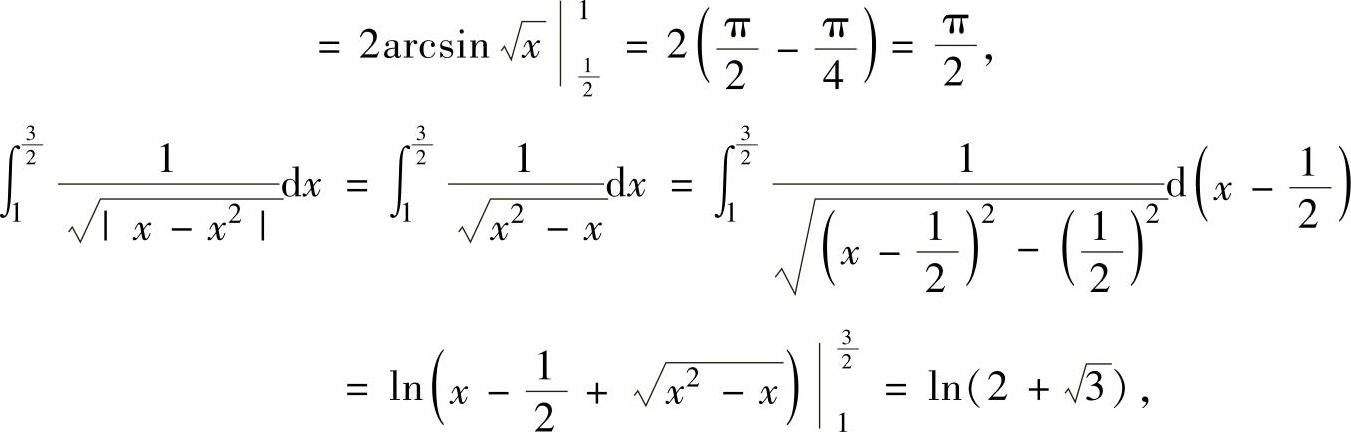
所以，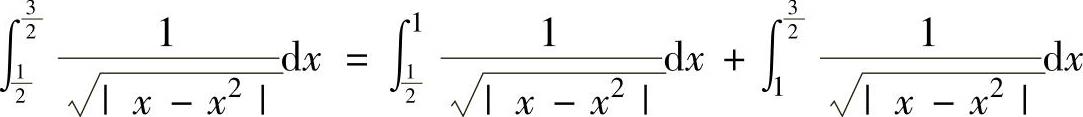
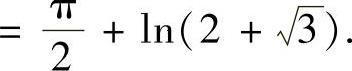
例2.11.5 求反常积分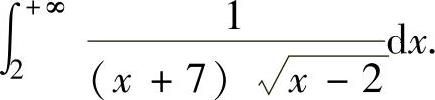
精解 由于所给的反常积分既是无穷限反常积分，又是无界函数反常积分（其中，x=2是瑕点），所以需分别计算反常积分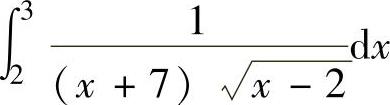
和∫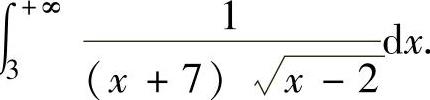
由于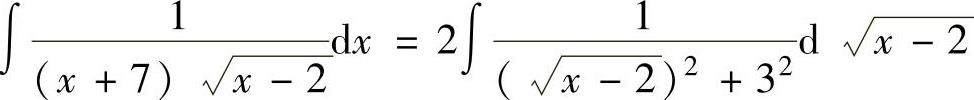
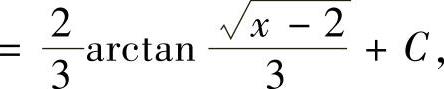
所以，
因此
