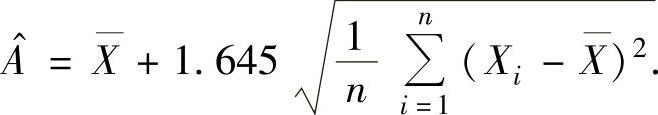参数的点估计方法
【主要内容】
1.参数点估计的概念
设总体X的概率分布形式已知,但含有未知参数θ,对θ的点估计就是借助总体X的简单随机样本X1,X2,…,Xn(观察值为x1,x2,…,xn),用适当的统计量θ^(X1,X2,…,Xn)作为θ的估计量,用θ^(X1,X2,…,Xn)的观察值θ^(x1,x2,…,xn)作为θ的估计值.
2.参数的点估计方法
参数点估计有两种常用方法:
(1)矩估计法
用样本矩作为相应的总体矩(包含待估参数θ)的估计量(或估计值),对θ作出点估计.这种方法称为参数θ的矩估计法.
(2)最大似然估计法
根据总体分布和样本构造似然函数(包含待估参数θ),取使似然函数达到最大值的θ^作为θ的估计量(或估计值).这种方法称为θ的最大似然估计法.
似然函数的作法如下:
设总体X是离散型随机变量,它的分布律P(X=x)=p(x;θ)(θ是待估参数),则此时的似然函数L(x1,x2,…,xn;θ)(或简记为L(θ))为
L(θ)=p(x1;θ)p(x2;θ)…p(xn;θ),其中x1,x2,…,xn是相应于来自总体X的简单随机样本X1,X2,…,Xn的观察值.
设总体X是连续型随机变量,它的概率密度为f(x;θ)(θ是待估参数),则此时的似然函数L(x1,x2,…,xn;θ)(或简记为L(θ))为
L(θ)=f(x1;θ)f(x2;θ)…f(xn;θ),其中x1,x2,…,xn是相应于来自总体X的简单随机样本X1,X2,…,Xn的观察值.
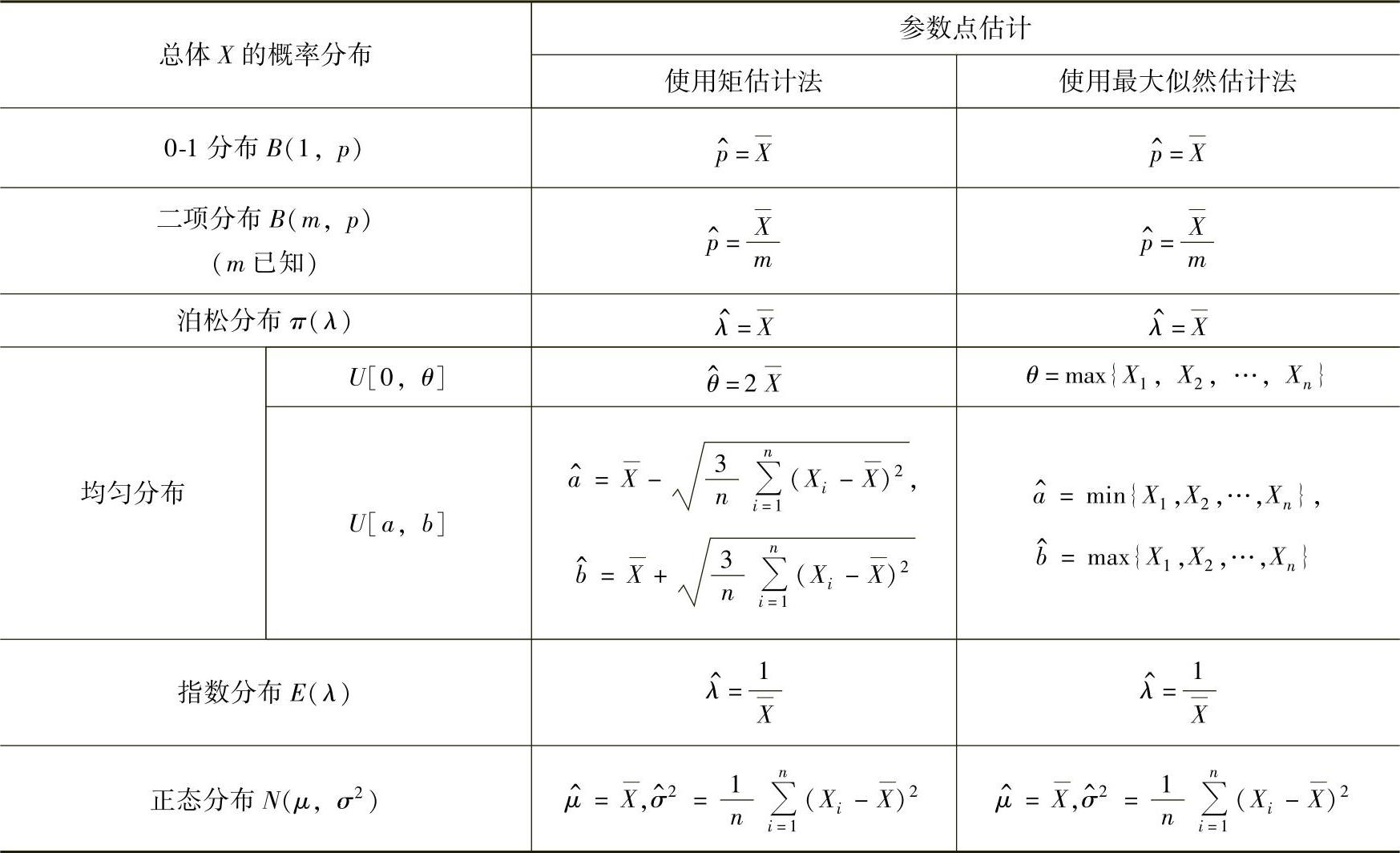
3.常用总体的参数点估计设(X1,X2,…,Xn)是来自总体X的一个简单随机样本,其中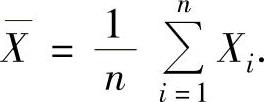
【典型例题】
例8.3.1 设总体X的概率密度为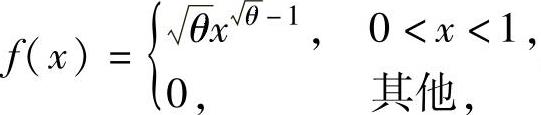 其中θ>0是未知参数,x1,x2,…,xn是来自总体X的一个样本观察值.分别用矩估计法和最大似然估计法计算θ的估计值.
其中θ>0是未知参数,x1,x2,…,xn是来自总体X的一个样本观察值.分别用矩估计法和最大似然估计法计算θ的估计值.
精解 (1)矩估计法.因为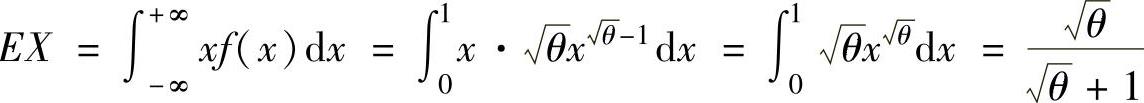 ,所以,由矩估计法得
,所以,由矩估计法得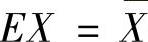 (其中
(其中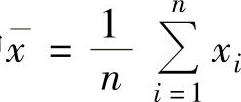 ),即
),即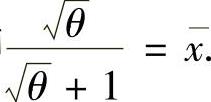 解此方程得
解此方程得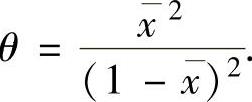 因此由矩估计法所得的
因此由矩估计法所得的
θ的估计值为
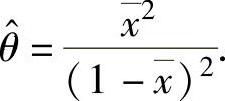
(2)最大似然估计法.
似然函数为L(θ)=f(x1)f(x2)…f(xn)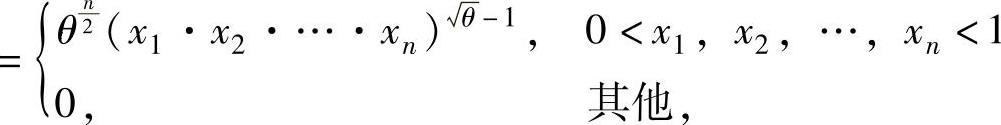 ,
,
显然,L(θ)只能在0<x1,x2,…,xn<1的点(x1,x2,…,xn)处取到最大值,故可取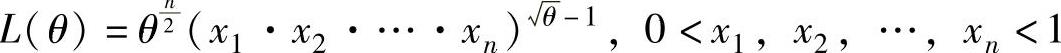 ,
,
即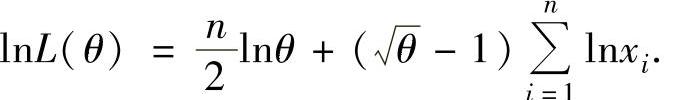
由最大似然估计法,令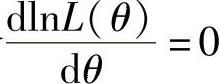 ,即
,即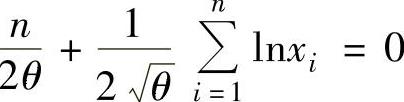 ,
,
此方程的解即为θ的最大似然估计值
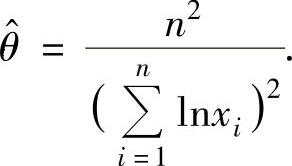
例8.3.2 设总体X的分布律为
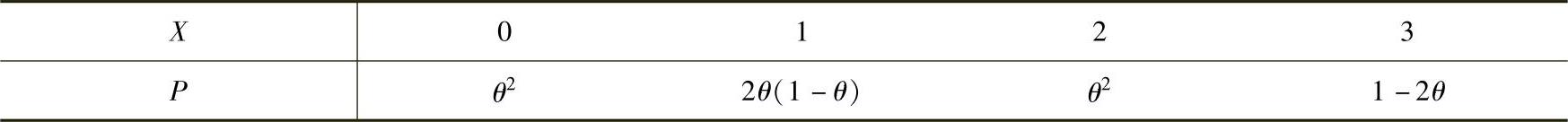
其中,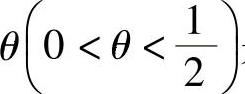 是未知参数.设3,1,3,0,3,1,2,3是X的一个样本观察值,分别
是未知参数.设3,1,3,0,3,1,2,3是X的一个样本观察值,分别
用矩估计法和最大似然估计法计算θ的估计值.
精解 (1)矩估计法.(https://www.daowen.com)
因为EX=0·θ2+1·2θ(1-θ)+2·θ2+3·(1-2θ)
=3-4θ,
所以,由矩估计法得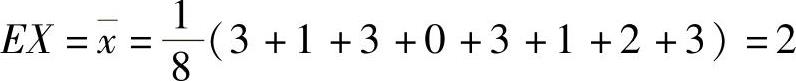 ,即3-4θ=2.
,即3-4θ=2.
解此方程得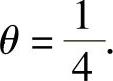 因此由矩估计法得θ的估计值为
因此由矩估计法得θ的估计值为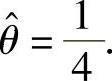
(2)最大似然估计法.
似然函数L(θ)=P(X=0)·[P(X=1)]2·P(X=2)·[P(X=3)]4
=θ2·[2θ(1-θ)]2·θ2·(1-2θ)4=4θ6(1-θ)2(1-2θ)4,即lnL(θ)=ln4+6lnθ+2ln(1-θ)+4ln(1-2θ).
由最大似然估计法,令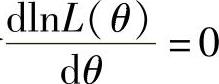 ,即
,即
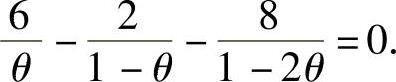
此方程位于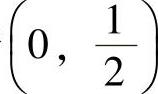 内的解,即为θ的最大似然估计值
内的解,即为θ的最大似然估计值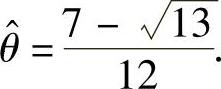
例8.3.3 设X1,X2,…,Xn是来自总体X的简单随机样本,其中X的概率密度为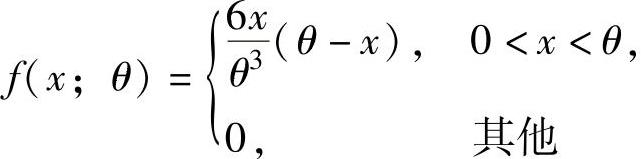 (θ是未知参数).
(θ是未知参数).
求参数θ的矩计量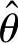 ,并计算D
,并计算D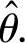
精解 因为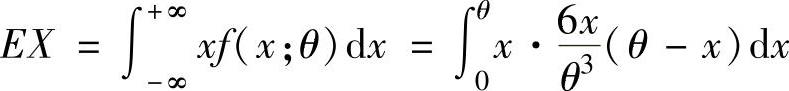
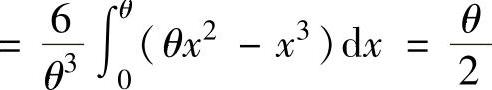 ,
,
所以,由矩估计法得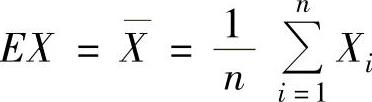 ,即
,即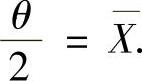 所以θ的矩估计量
所以θ的矩估计量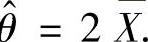
下面计算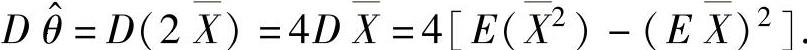
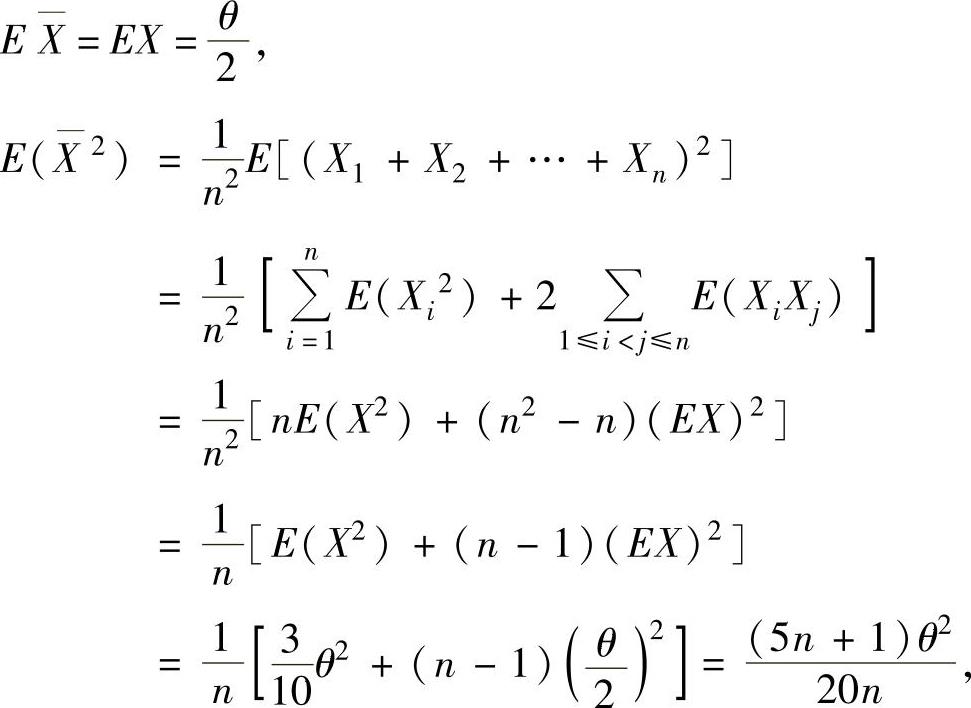 其中
其中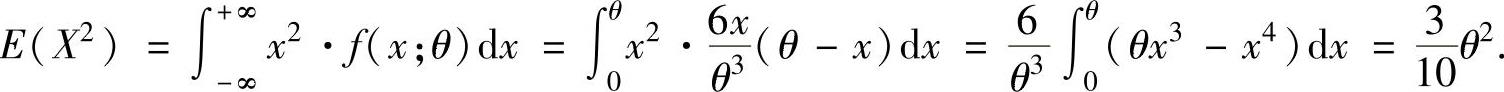 所以,
所以,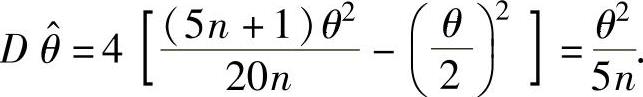
例8.3.4 设某种元件的使用寿命X的概率密度为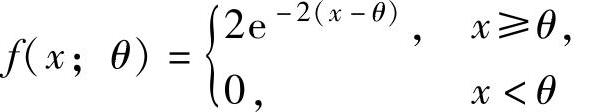 (其中θ是未知参数),
(其中θ是未知参数),
又设X1,X2,…,Xn(n>1)是来自总体X的简单随机样本,求:
(1)θ的矩估计量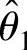 ;
;
(2)θ的最大似然估计量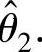
精解 (1)由于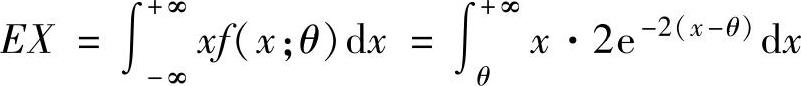
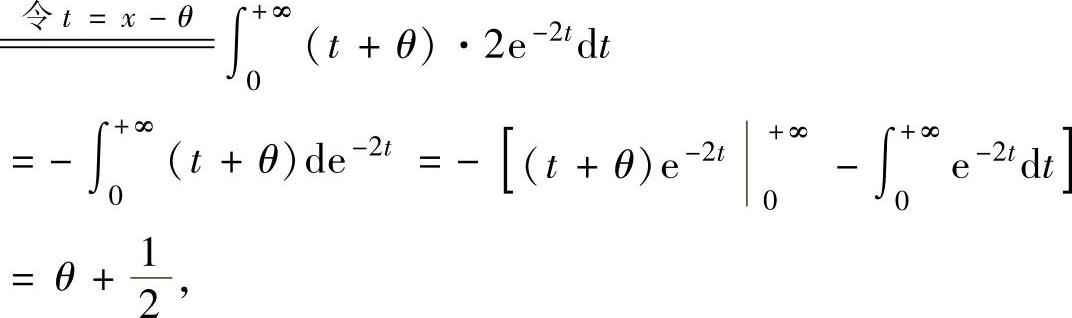
所以,由矩估计法得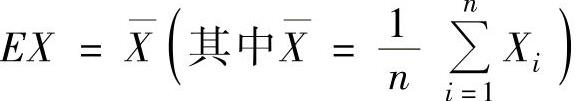 ,即
,即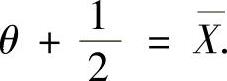 所以θ的矩估计量
所以θ的矩估计量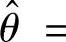
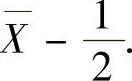
(2)设x1,x2,…,xn是样本X1,X2,…,Xn的观察值,则似然函数为L(θ)=f(x1)f(x2)…f(xn)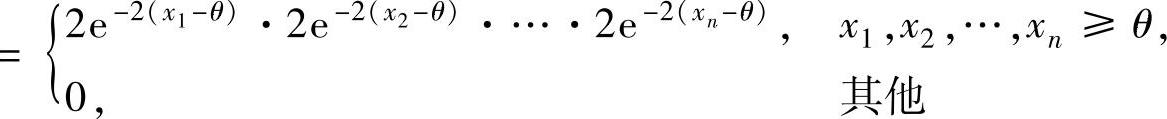

显然,L(θ)的最大值只能在x1,x2,…,xn≥θ处取到,所以可取
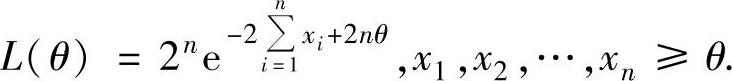
由于L(θ)是θ的单调增加函数,所以当θ=min{x1,x2,…,xn}时,L(θ)取最大值.因此由θ的最大似然估计量为
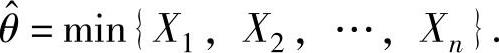
例8.3.5 设总体X~N(μ,σ2),X1,X2,…,Xn是它的一个简单随机样本,求使得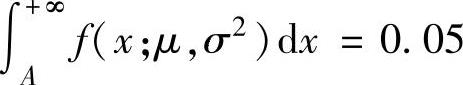 的点A的最大似然估计量,其中f(x;μ,σ2)是X的概率密度,μ,σ2是未知参数.
的点A的最大似然估计量,其中f(x;μ,σ2)是X的概率密度,μ,σ2是未知参数.
精解 将A表示成关于μ,σ2的函数,然后用μ,σ2的最大似然估计量算出A的最大似然估计量.
由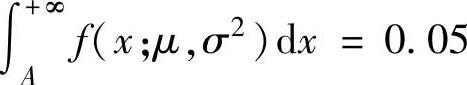 ,即
,即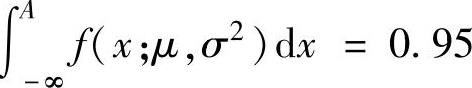 得
得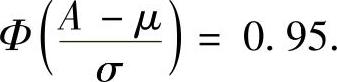 查表得
查表得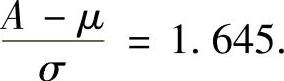 于是A的最大似然估计量为
于是A的最大似然估计量为
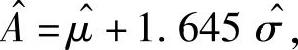
其中,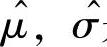 是μ,σ的最大似然估计量,它们分别为
是μ,σ的最大似然估计量,它们分别为
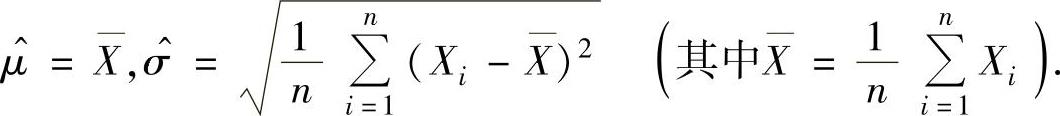
所以,A的最大似然估计量为