六、矩阵相似

六 、矩阵相似

【主要内容】

1.矩阵相似的定义

设A，B都是n阶矩阵.如果存在n阶可逆矩阵P，使得B=P^-1AP，则称矩阵A与B相似，也称A与B为相似矩阵，记为A～B.

2.矩阵相似的性质

设A，B，C都是n阶矩阵，则有以下性质：

（1）A～A.

（2）如果A～B，则B～A.

（3）如果A～B，B～C，则A～C.

（4）如果A～B，则A^T～B^T，A^m～B^m（其中，m是正整数），λA～λB（其中，λ是常数），φ（A）～φ（B）（其中，φ（λ）=a₀+a₁λ+…+a_mλ^m是关于λ的多项式）.

（5）如果A～B，则A=B，从而A，B同为可逆或不可逆.

（6）如果A～B，则当A可逆时，A^-1～B^-1，A∗～B∗.

（7）如果A～B，则λE_n-A=λE_n-B，从而A，B有相同的特征值，trA=trB，且当ξ是A的对应特征值λ的特征向量时，B有对应特征值λ的特征向量P^-1ξ（其中，P是满足P^-1AP=B的可逆矩阵）.

（8）如果A～B，则A、B等价，从而r（A）=r（B）.

注 设A，B都是n阶矩阵，则以下两点值得注意：

（ⅰ）当A与B有相同特征值时，A与B未必相似；

（ⅱ）当A与B等价时，A与B未必相似.

【典型例题】

例6.6.1 （单项选择题）设矩阵A与B相似，其中

则矩阵A-3E₄与A²-E₄的秩之和为（ ）.

A.4 B.5 C.6 D.7

精解 由于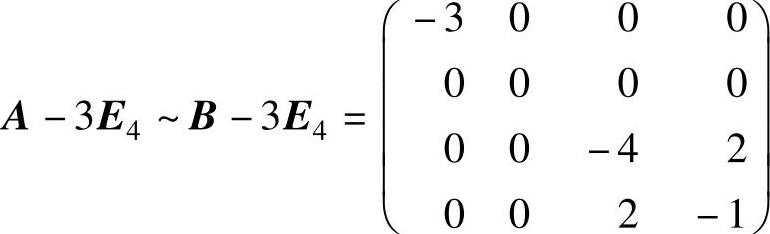仅有不为零的二阶子式，所以它的秩为2.从

而r（A-3E₄）=r（B-3E₄）=2.

由于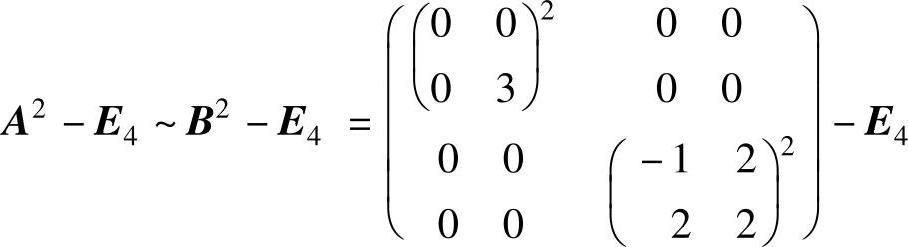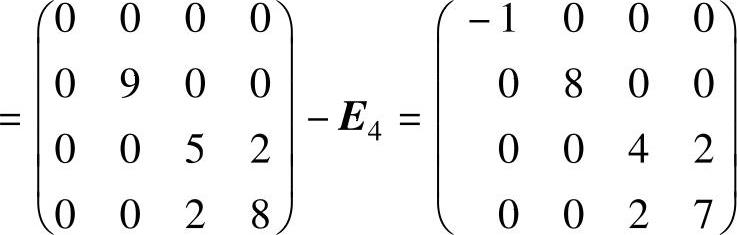，它的行列式不为零，所以它的秩为4.

从而r（A²-E₄）=r（B²-E₄）=4.

由此可知r（A-3E₄）+r（A²-E₄）=2+4=6.

因此本题选C.

例6.6.2 （单项选择题）设A是四阶矩阵，满足A²+A=O₄.如果r（A）=3，则与A相似的矩阵只能是（ ）.

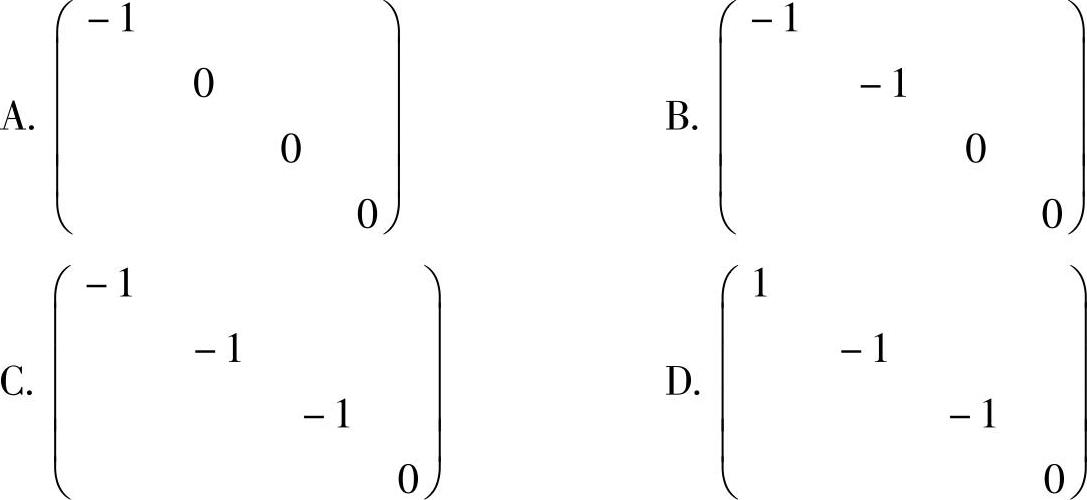
精解 设A的特征值为λ，则由题设A²+A=O₄知λ满足λ²+λ=0，因此，A的特征值λ只能取0或-1.

显然，只有选项A，B，C的矩阵特征值为0与-1，但其中仅有选项C的矩阵的秩为3，所以与A相似的矩阵只可能是选项C的矩阵.

因此本题选C.

例6.6.3 已知三阶矩阵A与3维列向量x，Ax，A²x线性无关，且A³x=3Ax-2A²x.

（1）记P=（x，Ax，A²x），求三阶矩阵B，使得A=PBP^-1，并求A的特征值；

（2）证明：对任意实数t，A³+tE₃与B³+tE₃相似.

精解 （1）B=P^-1AP=P^-1A（x，Ax，A²x）

=P^-1（Ax，A²x，A³x）

=P^-1（Ax，A²x，3Ax-2A²x）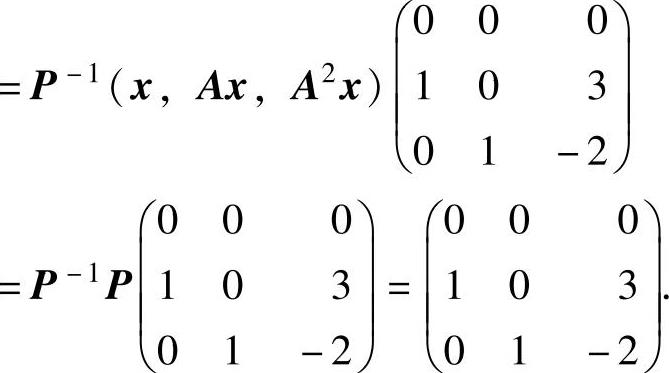

由于A～B，所以

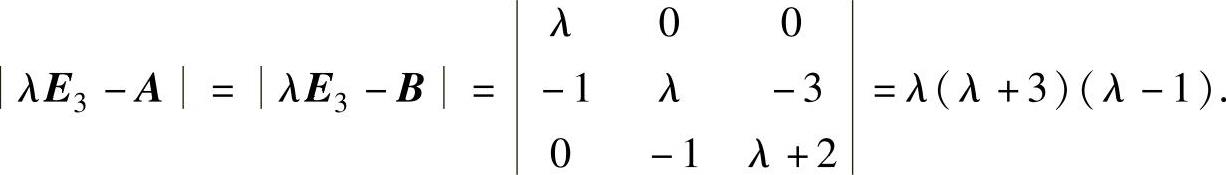
因此，A的特征值为λ=-3，0，1.

（2）利用矩阵相似的定义证明A³+tE₃～B³+tE_3.

由于有可逆矩阵P，使得

P^-1AP=B.所以，对于任意实数t有

P^-1（A³_+tE₃）P=P^-1A³P+tP^-1E₃P

=（P^-1AP）（P^-1AP）（P^-1AP）+tE₃=B³+tE₃，即A³+tE₃～B³+tE₃.

例6.6.4 设矩阵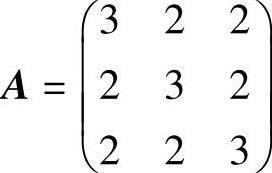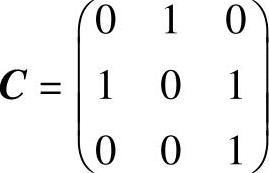，，B=C^-1A∗C，求

（1）矩阵A的所有特征值与特征向量；

（2）矩阵B的所有特征值与特征向量.

精解 （1）由λE₃-A=0，算出A的特征值，然后对各个特征值求齐次线性方程组（λE₃-A）x=0的非零解，得到对应的特征向量.由于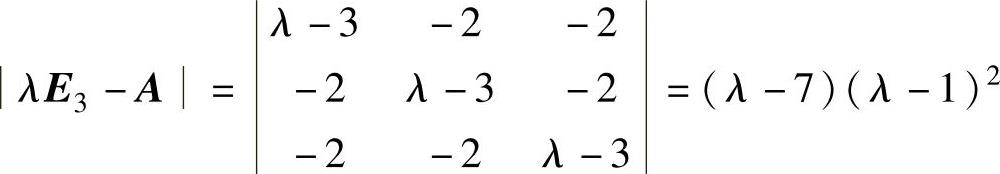，所以，A的特征值为λ₁=7，λ₂=1（二重），从而A=7×1²=7.

设A的对应λ₁=7的特征向量为x=（x₁，x₂，x₃）T，则x满足（7E₃-A）x=0，即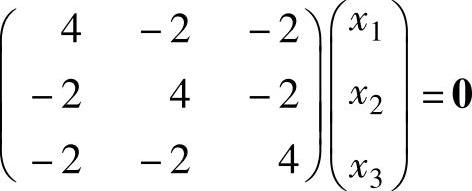，（1）由于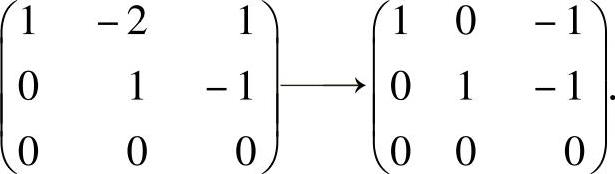所以，式（1）与方程组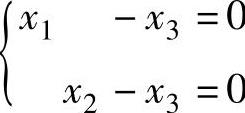，同解，从而式（1）有基础解系x=（1，1，1）^T.因此，A的对应特征值λ₁=7的所有特征向量为

c₁（1，1，1）^T=（c₁，c₁，c₁）^T（其中，c₁是任意非零常数）.

设A的对应λ₂=1的特征向量为y=（y₁，y₂，y₃）^T，则由A是实对称矩阵知

（x，y）=0，即y₁+y₂+y₃=0.该方程有基础解系（-1，1，0）^T与（-1，0，1）^T.因此A的对应λ₂=1的所有特征向量为c₂（-1，1，0）^T+c₃（-1，0，1）=（-c₂-c₃，c₂，c₃）^T（其中，c₂，c₃是任意不全为零的常数）.

（2）先算出A∗的所有特征值与特征向量，然后利用B=C^-1A∗C得到B的所有特征值与特征向量.

A∗的特征值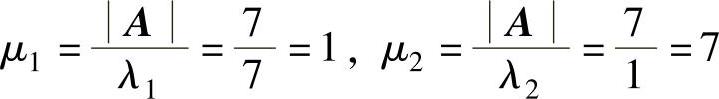（二重），且对应μ₁的所有特征向量为（c₁，c₁，c1）^T（其中，c₁是任意非零常数），对应μ₂=7的所有特征向量为（-c₂-c₃，c₂，c₃）^T（其中，c₂，c₃是任意不全为零的常数）.

B的所有特征值为ν₁=1，ν₂=7（二重）.为了计算它们对应的所有特征向量，先计算C^-1.由于

所以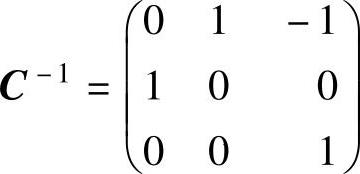，，从而B的对应ν₁=1的所有特征向量为，

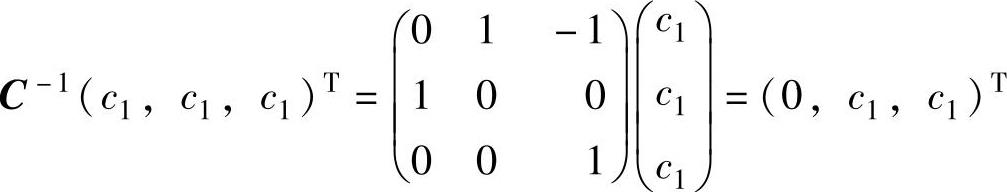对应ν₂=7的所有特征向量为

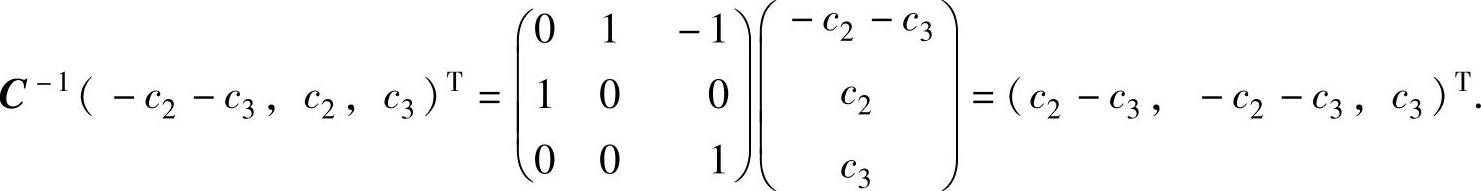
注 本题题解表明，要计算A∗，A^-1，f（A）（f（λ）是关于λ的多项式），P^-1AP（P是可逆矩阵）等比较复杂矩阵的特征值与特征向量，可从计算A的特征值与特征向量入手，然后利用特征值与特征向量的性质，得到A∗，A^-1，f（A），P^-1AP等的特征值与特征向量.