向量组的极大线性无关组与秩
【主要内容】
1.向量组的极大线性无关组的概念
如果向量组α1，α2，…，αm的部分组αi1，αi2，…，αir满足以下两个条件：
（1）αi1，αi2，…，αir线性无关.
（2）α1，α2，…，αm中的任一个向量都可由αi1，αi2，…，αir线性表示，则称αi1，αi2，…，αir是α1，α2，…，αm的一个极大线性无关组，简称极大无关组.
极大线性无关组的性质：
（1）向量组与它的任一个极大无关组等价.
（2）向量组的任意两个极大无关组等价.
（3）向量组的每个极大无关组都含相同个数的向量.
2.向量组的秩的概念
向量组α1，α2，…，αm的极大无关组中所含的向量个数称为该向量组的秩，记为r（α1，α2，…，αm）.
向量组秩的性质：
（1）矩阵行向量组与列向量组的秩相等，且都等于该矩阵的秩.因此向量组的秩，可以通过对应的矩阵（即将所给的向量组作为行向量组或列向量组构成的矩阵）的秩的计算得到.
对两个m×n矩阵A，B，r（A）=r（B）的充分必要条件是A与B等价.
（2）设向量组α1，α2，…，αs可由向量组β1，β2，…，βr线性表示，则r（α1，α2，…，αs）≤r（β1，β2，…，βr）.
（3）设向量组α1，α2，…，αs与向量组β1，β2，…，βr等价，则r（α1，α2，…，αs）=r（β1，β2，…，βr）.
（4）已知r（α1，α2，…，αs）=r，则向量组α1，α2，…，αs中任意r个线性无关向量就是该向量组的一个极大无关组，特别地，当
r（α1，α2，…，αs）=s时，向量组α1，α2，…，αs线性无关.
【典型例题】
例5.8.1 设向量组α1=（1+a，1，1，1）T，α2=（2，2+a，2，2）T，α3=（3，3，3+a，3）T，α4=（4，4，4，4+a）T，问a为何值时，α1，α2，α3，α4线性相关？求此时的所有极大线性无关组.
精解 由于向量组是由4个4维向量组成，所以从考虑A=（α1，α2，α3，α4）的行列
式入手.
由于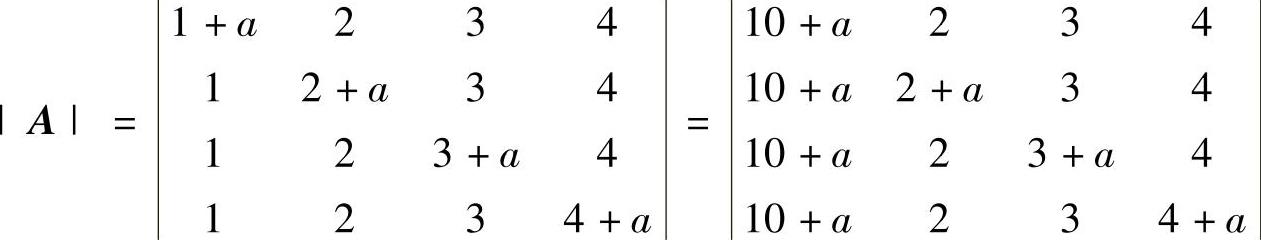
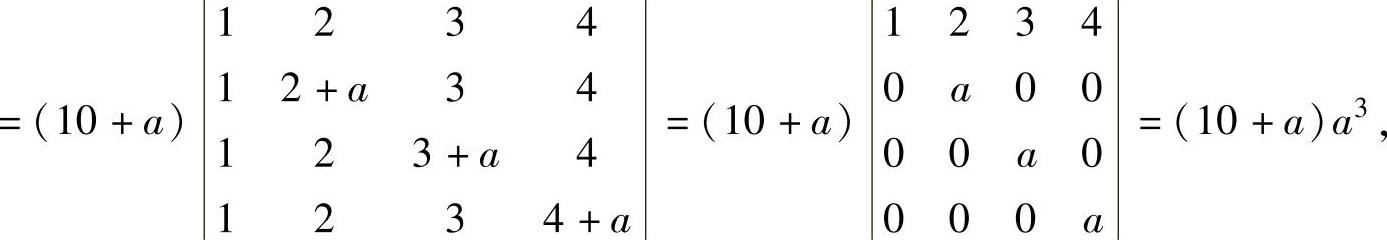
所以，由|A|=0得a=0，-10，即当a=0，-10时，α1，α2，α3，α4线性相关.
当a=0时，
此时，α1，α2，α3，α4中的任一向量都是一个极大线性无关组.
当a=-10时，由
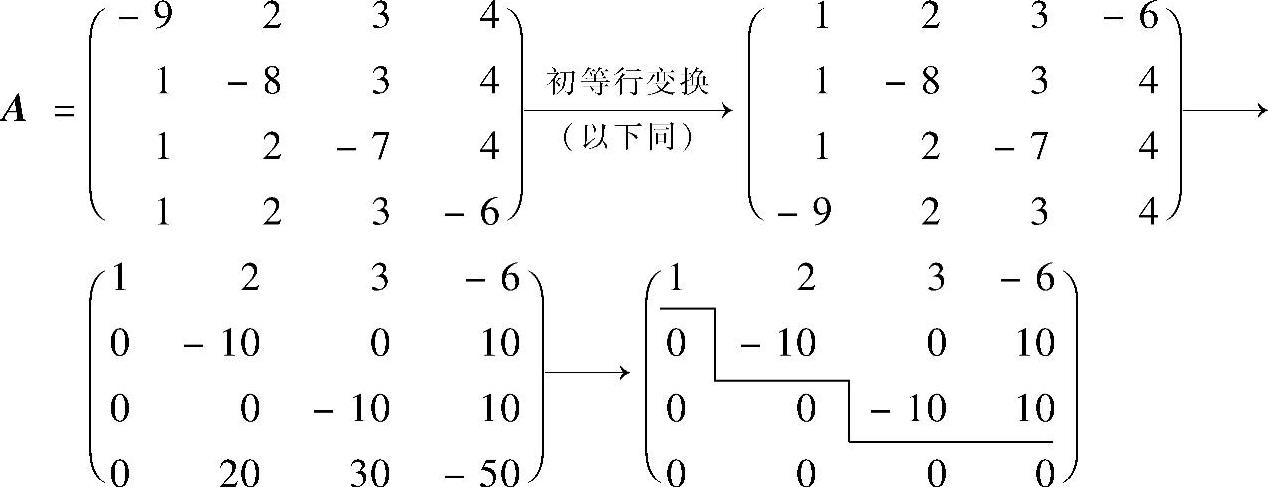
知r（A）=3.由于此时α1+α2+α3+α4=0，所以α1，α2，α3，α4中任意3个向量都是一个极大线性无关组.
例5.8.2 已知向量组β1=（0，1，-1）T，β2=（a，2，1）T，β3=（b，1，0）T与向量组α1=（1，2，-3）T，α2=（3，0，1）T，α3=（9，6，-7）T具有相同的秩，且β3可由α1，α2，α3线性表示，求参数a，b的值.
精解 显然α1，α2线性无关，但由α3=3α1+2α2知α1，α2，α3线性相关.因此r（α1，α2，α3）=2.于是由题设知r（β1，β2，β3）=2，即β1，β2，β3线性相关.由此得到由β1，β2，β3作为列构成的行列式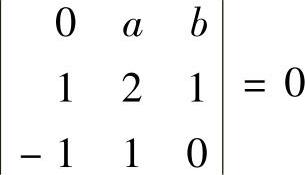
，即a=3b.（1）
此外，由β3可由α1，α2，α3线性表示知，β3可由α1，α2线性表示，即α1，α2，β3线性相关，所以，以α1，α2，β3作为列构成的行列式
，即b=5.（2）将式（2）代入式（1）得a=15.
例5.8.3 已知3个向量组（Ⅰ）：α1，α2，α3；（Ⅱ）：α1，α2，α3，α4；（Ⅲ）：α1，α2，α3，α5的秩分别为3，3，4.证明：向量组α1，α2，α3，α4-α5的秩为4.
精解 显然，只要证明α1，α2，α3，α4-α5线性无关即可.
假设存在数k1，k2，k3，k4使得
k1α1+k2α2+k3α3+k4（α4-α5）=0，（1）即k1α1+k2α2+k3α3+k4α4-k4α5=0.（2）
由（Ⅰ）的秩为3知α1，α2，α3线性无关，所以由（Ⅱ）的秩为3知α4可由α1，α2，α3线性表示，记为
α4=λ1α1+λ2α2+λ3α3.（3）
将式（3）代入式（2）得
k1α1+k2α2+k3α3+k4（λ1α1+λ2α2+λ3α3）-k4α5=0，即（k1+λ1k4）α1+（k2+λ2k4）α2+（k3+λ3k4）α3-k4α5=0.（4）
由题设知（Ⅲ）的秩为4，即α1，α2，α3，α5线性无关，所以式（4）中的系数全为零，即有
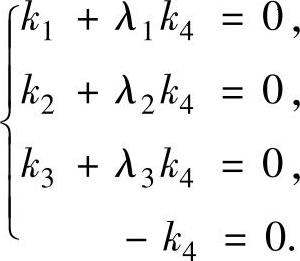
由此得到式（1）中的k1=k2=k3=k4=0，因此α1，α2，α3，α4-α5线性无关，它的秩为4.
例5.8.4 设矩阵
（其中，α1，
α2，α3，α4是A的列向量组），求A的列向量组的一个极大线性无关组，并求与其余列向量对应的极大线性无关组的线性表达式.
精解 记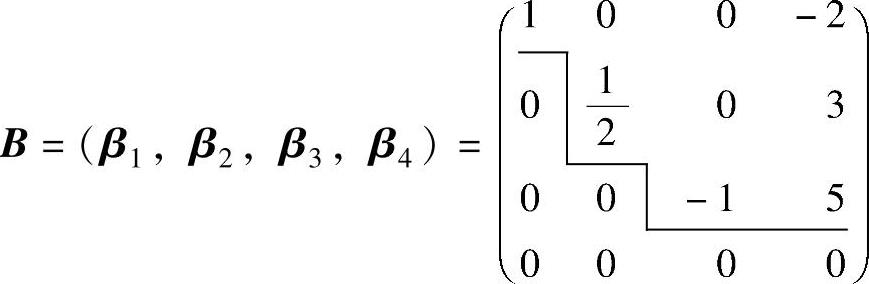
，由阶梯形矩阵知β1，β2，β3是B的列向量组的一个极大线性无关组，且
β4=-2β1+6β2-5β3.
由于B是A经初等行变换得到的矩阵，且α1，α2，α3，α4是A的列向量组，所以α1，α2，α3是α1，α2，α3，α4的一个极大线性无关组，且
α4=-2α1+6α2-5α3.
注 当同时要求向量组（Ⅰ）的极大线性无关组及与其余向量对应的极大线性无关组的线性表达式时，可将该向量组作为某个矩阵A的列向量组，对A施行初等行变换化为阶梯形矩阵B，则有以下两个结论：
（1）B中每一个非零行的第1个非零元素所在的列向量即为B的列向量组的一个极大线性无关组，而其余的列向量都可由这个极大线性无关组表示.例如，上例中的β1，β2，β3是关于β1，β2，β3，β4的一个极大线性无关组，且有
β4=-2β1+6β2-5β3.
（2）A中与B的极大线性无关组对应的列向量构成A的列向量组（即所给的向量组（Ⅰ））的一个极大线性无关组，并且它的其余的每个向量都可由这个极大线性无关组线性表示，而且表达式与B的其余列向量表达式对应相等.例如，上例中α4的关于α1，α2，α3的线性表达式与β4=-2β1+6β2-5β3相同，即
α4=-2α1+6α2-5α3.
例5.8.5 （单项选择题）设n维列向量组α1，α2，…，αm（m<n）线性无关，则n维列向量组β1，β2，…，βm线性无关的充分必要条件是（ ）.
A.向量组α1，α2，…，αm可由向量组β1，β2，…，βm线性表示
B.向量组β1，β2，…，βm可由向量组α1，α2，…，αm线性表示
C.向量组α1，α2，…，αm与向量组β1，β2，…，βm等价
D.矩阵A=（α1，α2，…，αm）与矩阵B=（β1，β2，…，βm）等价
精解 先考虑选项A，B，C.
设向量组α1=（1，0，0）T，α2=（0，1，0）T，显然，它们线性无关，向量组β1=（1，0，0）T，β2=（0，0，1）T也线性无关，向量组α1，α2不能由向量组β1，β2线性表示，同样向量组β1，β2也不能由向量组α1，α2线性表示.所以选项A，B，C都不能选.
因此本题选D.
注 （i）选项D是正确的，现证明如下：
必要性.设β1，β2，…，βm线性无关，则r（B）=r（β1，β2，…，βm）=m，另由题设知r（A）=r（α1，α2，…，αm）=m，即A，B有相同的秩，从而A与B等价.
充分性.设A与B等价，则r（β1，β2，…，βm）=r（B）=r（A）=r（α1，α2，…，αm）=m，从而β1，β2，…，βm线性无关.
（ii）由本题可以得出以下结论：
设A，B都是m×n矩阵，则r（A）=r（B）是A与B等价的充分必要条件；设两个n维向量组（Ⅰ）：α1，α2，…，αm和（Ⅱ）：β1，β2，…，βm，则r（A）=r（B）是（Ⅰ）与（Ⅱ）等价的充分而非必要条件.